- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Графический способ решения систем уравнений
Содержание
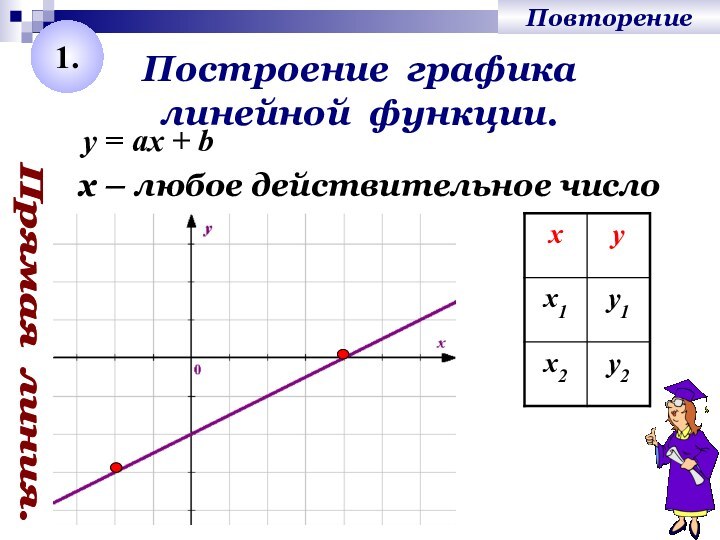
- 2. Построение графика линейной функции. Прямая линия.y = ах + bх – любое действительное число1.Повторение
- 3. Построение графика функции обратной пропорциональности.1.Определить, в каких
- 4. Построение графика функции3.1.х – любое действительное число.2.k
- 5. Повторение4.Построение окружности.r – радиус окружности.(x0; у0 )– координатыцентра окружности.
- 6. Построение графика функции у = ах2 + bх +с.1.Определить направление ветвей параболы.Парабола.5.2.х – любое действительное число.Повторение
- 7. Построение графика функции у = ах2 +
- 8. Построение графика функции у = ах2 +
- 9. Построение графика функции у = ах2 +
- 10. Задание 1.Решить графически систему уравнений.1.2.Построим графикифункций в однойсистеме координат.3.Составим таблицы значений функций.
- 11. Задание 1.Ответ: ( -1; 1); (3; 9) АВ
- 12. Задание 2.Решить графически систему уравнений.1.2.Построим графикифункций в однойсистеме координат.3.Составим таблицы значений функций.
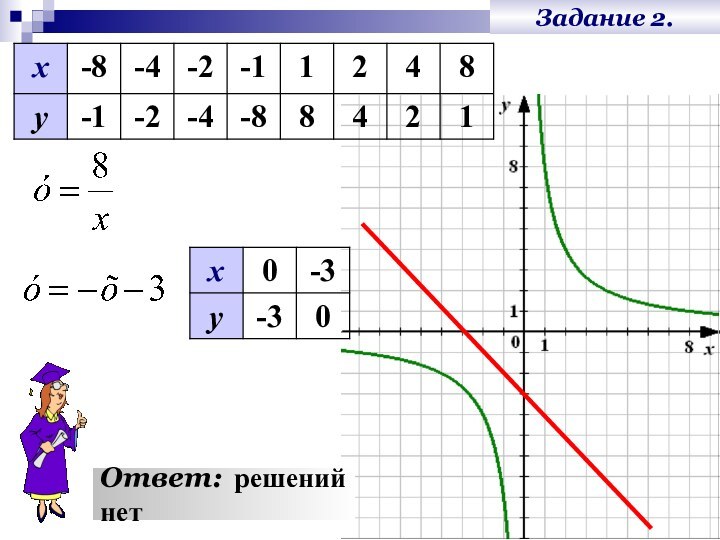
- 13. Задание 2.Ответ: решений нет
- 14. Задание 3.Решить графически систему уравнений.Подробно
- 15. х – любое действительное число.1.2.Графиком функции является
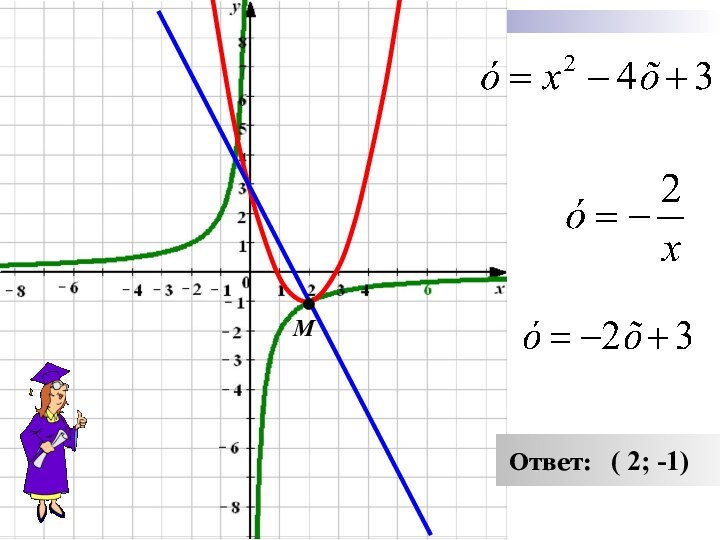
- 16. М Ответ: ( 2; -1)
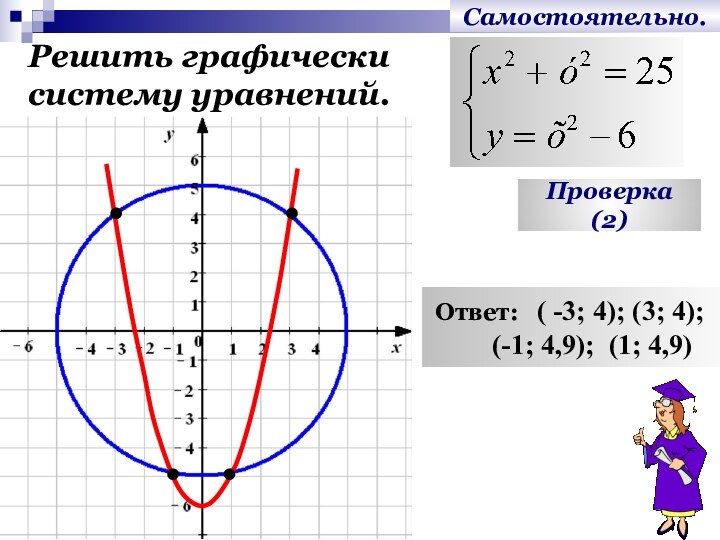
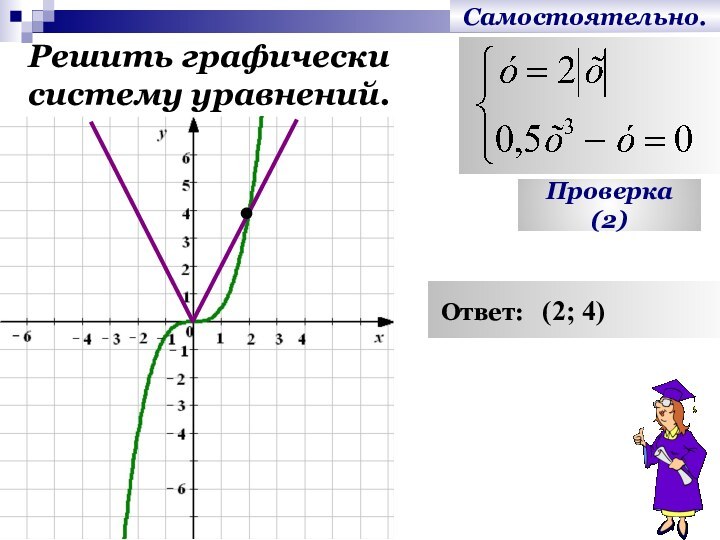
- 17. Самостоятельно.Решить графически систему уравнений.Проверка (2) Ответ:
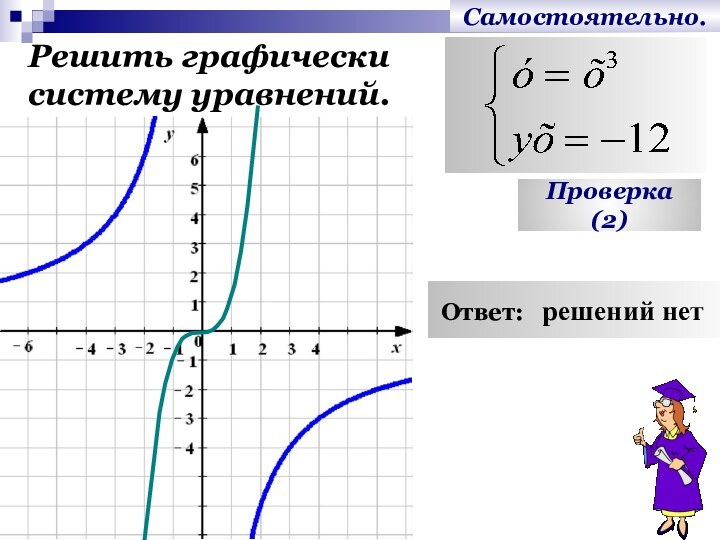
- 18. Самостоятельно.Решить графически систему уравнений.Проверка (2) Ответ: решений нет
- 19. Скачать презентацию
- 20. Похожие презентации
Построение графика линейной функции. Прямая линия.y = ах + bх – любое действительное число1.Повторение






Слайд 3
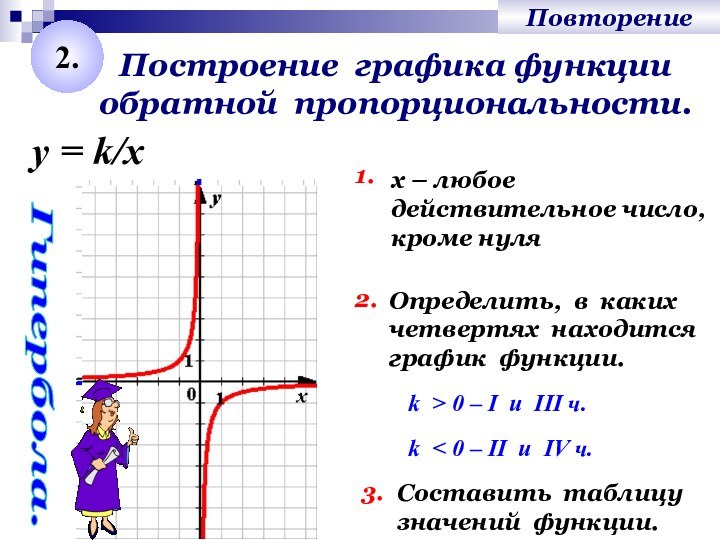
Построение графика функции обратной пропорциональности.
1.
Определить, в каких
четвертях
находится
график функции.
2.
Составить таблицу
значений функции.
Гипербола.
у = k/x
k > 0 –
I u III ч.k < 0 – II u IV ч.
3.
х – любое
действительное число,
кроме нуля
2.
Повторение
Слайд 4
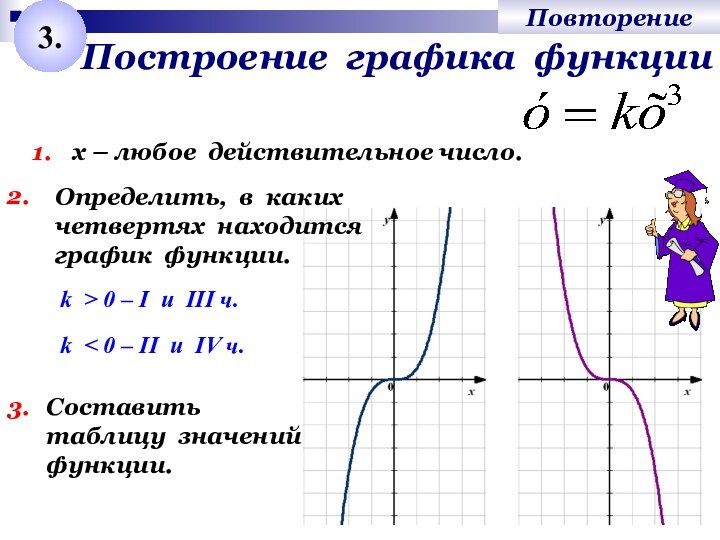
Построение графика функции
3.
1.
х – любое действительное число.
2.
k >
0 – I u III ч.
k < 0 –
II u IV ч.Определить, в каких
четвертях находится
график функции.
Составить
таблицу значений
функции.
3.
Повторение
Слайд 5
Повторение
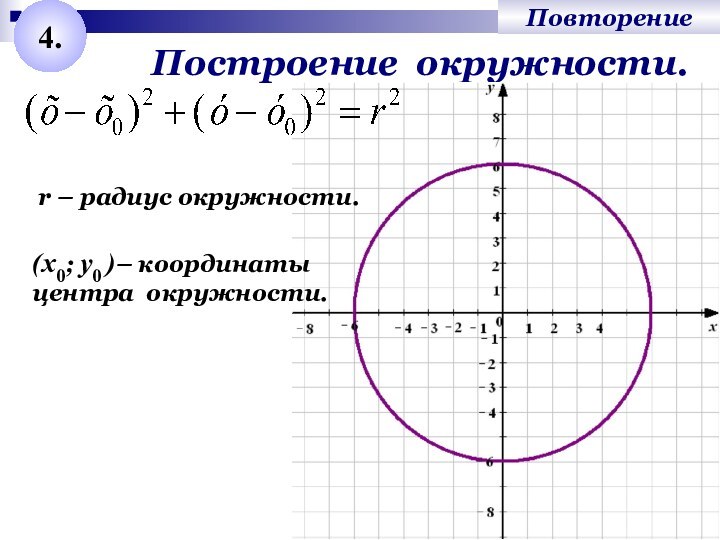
4.
Построение окружности.
r – радиус окружности.
(x0; у0 )– координаты
центра
окружности.
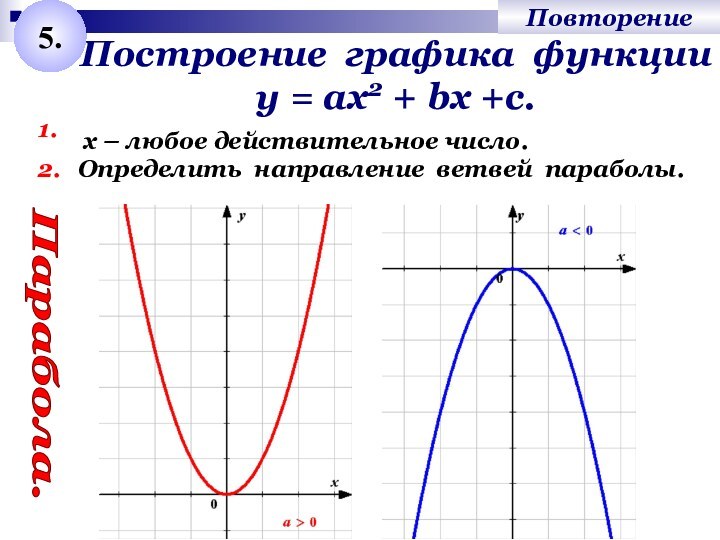
Слайд 6 Построение графика функции у = ах2 + bх
+с.
1.
Определить направление ветвей параболы.
Парабола.
5.
2.
х – любое действительное число.
Повторение
Слайд 7 Построение графика функции у = ах2 + bх
+с.
3.
Найти координаты вершины параболы
(т; п).
4.
Провести ось
симметрии.
О (т;п)
Повторение
5.
Слайд 8 Построение графика функции у = ах2 + bх
+с.
5.
Определить точки пересечения графика
функции с осью Ох, т.е.
найти нули функции.
(х1;0)
(х2;0)
Повторение
5.
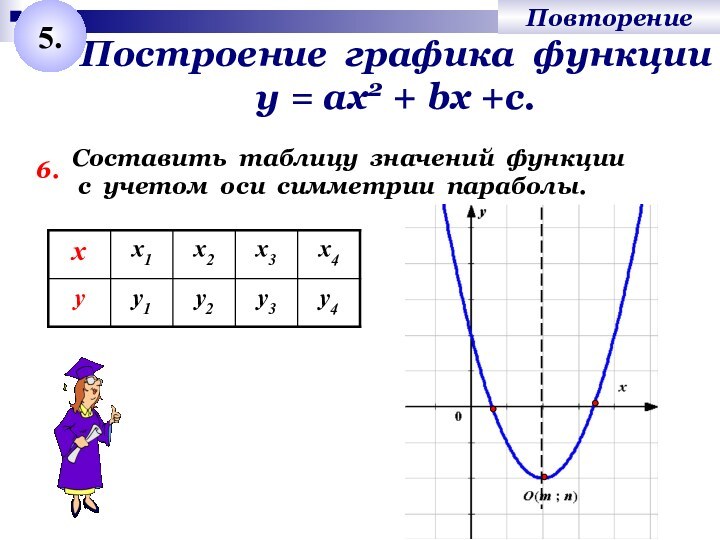
Слайд 9 Построение графика функции у = ах2 + bх
+с.
6.
Составить таблицу значений функции
с учетом оси симметрии параболы.
Повторение
5.
Слайд 10
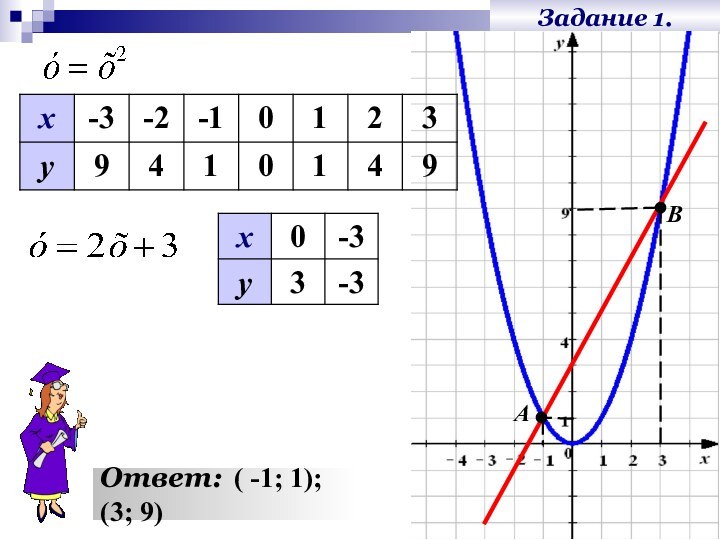
Задание 1.
Решить графически
систему уравнений.
1.
2.
Построим графики
функций в одной
системе координат.
3.
Составим
таблицы значений функций.
Слайд 12
Задание 2.
Решить графически
систему уравнений.
1.
2.
Построим графики
функций в одной
системе координат.
3.
Составим
таблицы значений функций.
Слайд 15
х – любое действительное число.
1.
2.
Графиком функции является парабола,
ветви
которой направлены вверх. a > 0
3.
Найдём координаты вершины параболы
4.
Дополнительные точки:
М ( 2; -1)





























