- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Графы
Содержание
- 2. Можно ли объехать станции метро, находящиеся в
- 4. ?
- 5. «Графы»
- 6. Топология -наука, которая раньше называлась «геометрией положения».
- 7. Задача Эйлера (1736 г.): «В Кенигсберге река,
- 8. Графом называется … вершины графа – это
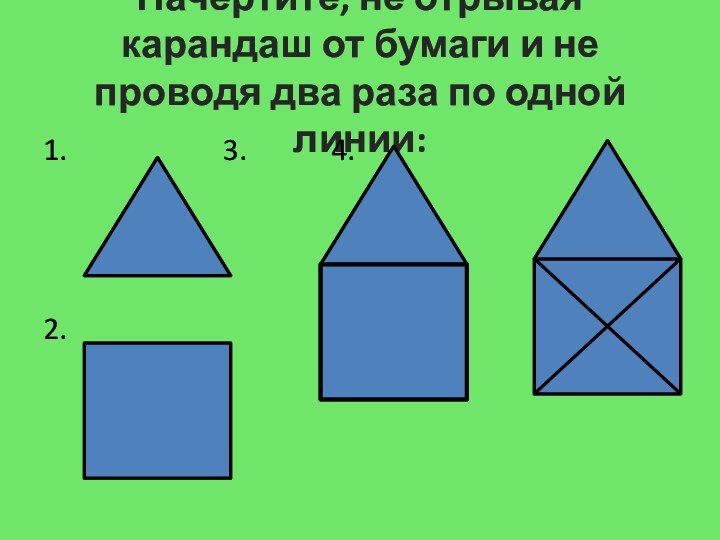
- 9. Начертите, не отрывая карандаш от бумаги и
- 10. План:Выяснить признаки фигуры, которую можно нарисовать;Найти начальную точку;Нарисовать всю фигуру
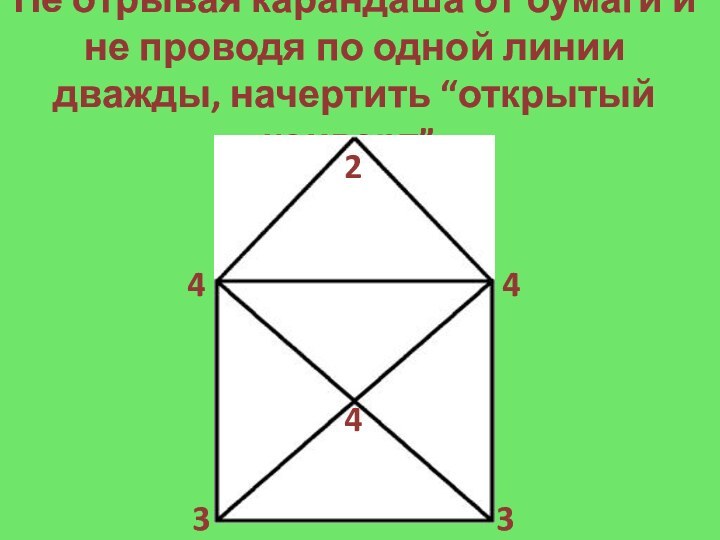
- 11. Не отрывая карандаша от бумаги и не проводя по одной линии дважды, начертить “открытый конверт”:
- 12. С чем мы справились?332222222222если нечетных точек в
- 13. Не отрывая карандаша от бумаги и не
- 14. Выводы:1. если нечетных точек в фигуре нет,
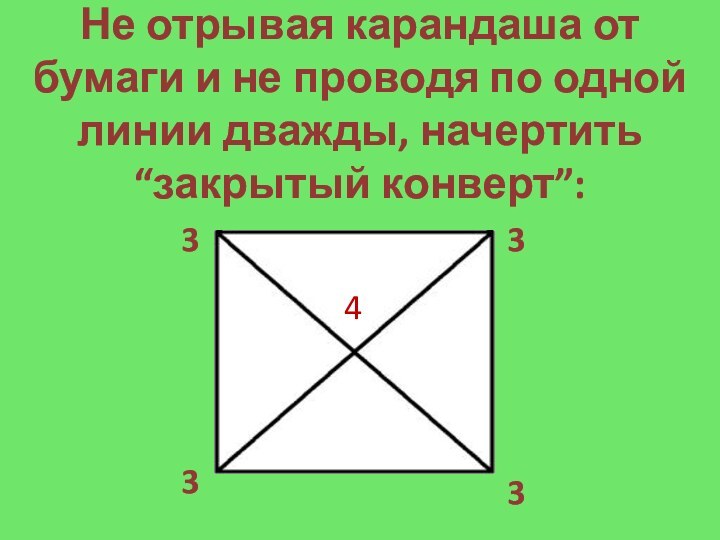
- 15. Не отрывая карандаша от бумаги и не проводя по одной линии дважды, начертить “закрытый конверт”: 33334
- 16. Выводы:1. если нечетных точек в фигуре нет,
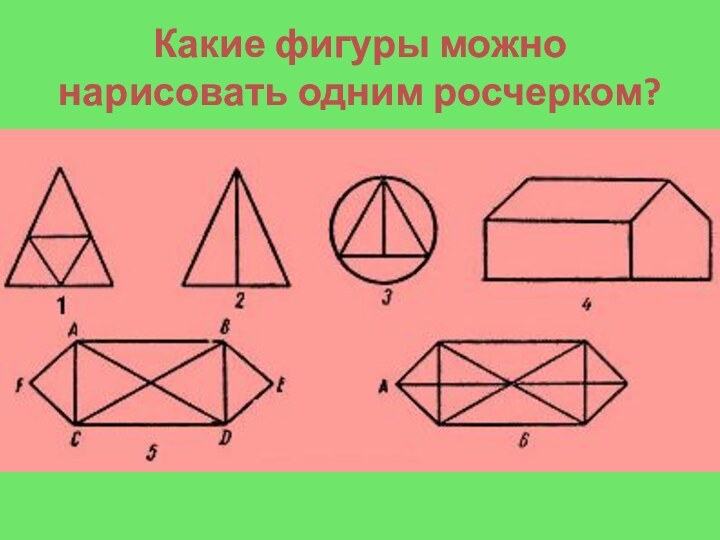
- 17. Какие фигуры можно нарисовать одним росчерком?
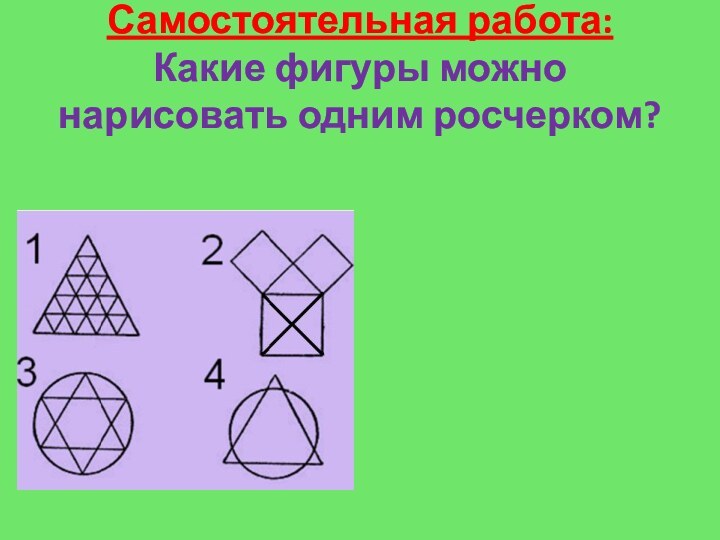
- 18. Самостоятельная работа: Какие фигуры можно нарисовать одним росчерком?
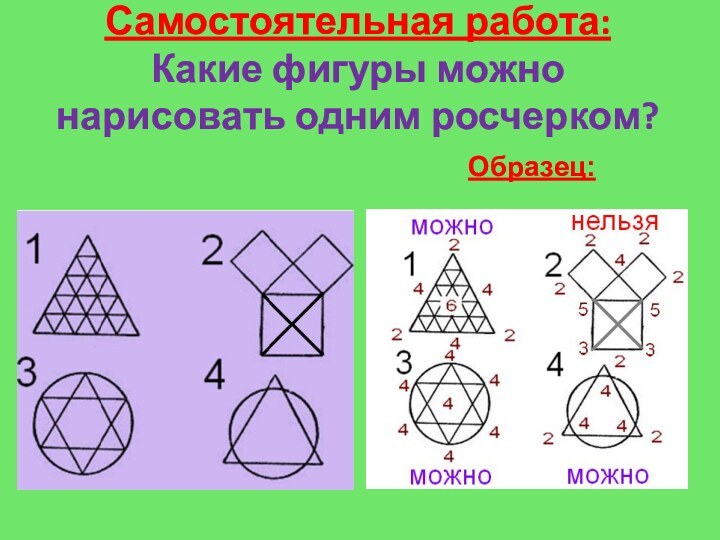
- 19. Самостоятельная работа: Какие фигуры можно нарисовать одним росчерком?Образец:
- 20. Задача Эйлера: «В Кенигсберге река, омывающая два
- 21. Мосты Санкт- ПетербургаЗадача: пройти по 17
- 22. Схема кольцевой линии московского метрополитена
- 23. Скачать презентацию
- 24. Похожие презентации
Можно ли объехать станции метро, находящиеся в границе кольцевой линии, лишь один раз посетив каждую из них?











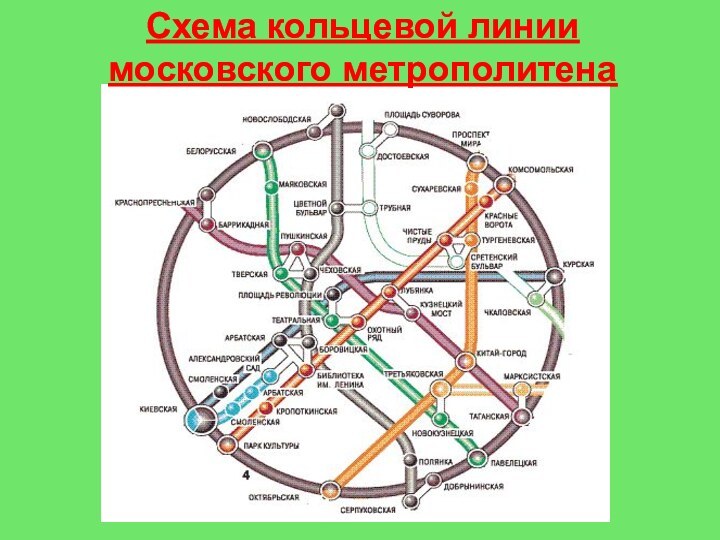

Слайд 2 Можно ли объехать станции метро, находящиеся в границе
кольцевой линии, лишь один раз посетив каждую из них?
Слайд 6 Топология -наука, которая раньше называлась «геометрией положения». Эта
отрасль геометрии занимается только порядком расположения частей фигуры друг
относительно друга, отвлекаясь от их размеровЛеонард Эйлер
(1707-1783)
Разделы топологии:
комбинаторная топология;
алгебраическая топология;
теоретико-множественная топология, изучающую множества как скопления точек.
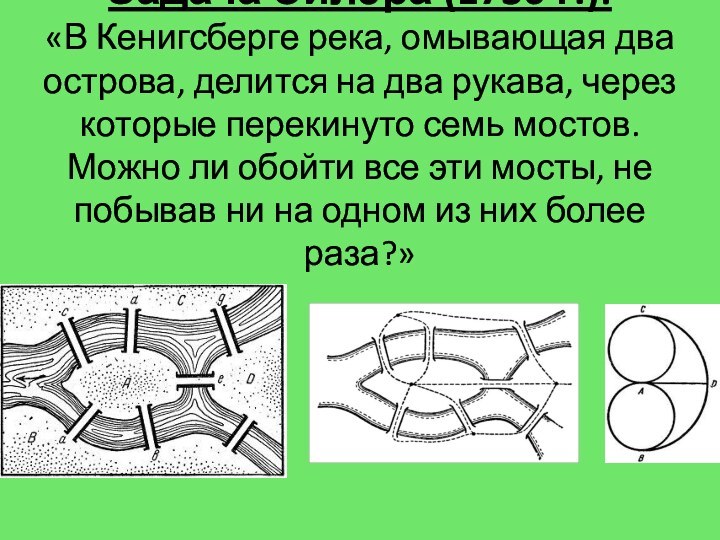
Слайд 7 Задача Эйлера (1736 г.): «В Кенигсберге река, омывающая два
острова, делится на два рукава, через которые перекинуто семь
мостов. Можно ли обойти все эти мосты, не побывав ни на одном из них более раза?»
Слайд 8
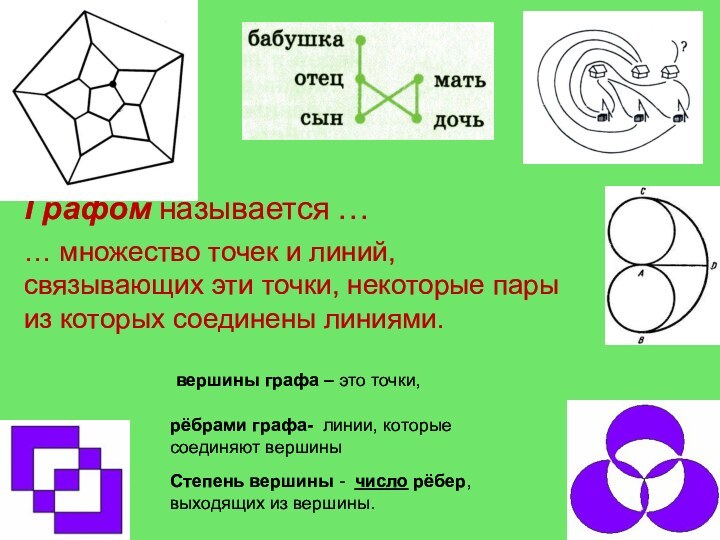
Графом называется …
вершины графа – это точки,
рёбрами графа- линии, которые соединяют вершины
Степень вершины -
число рёбер, выходящих из вершины.… множество точек и линий, связывающих эти точки, некоторые пары из которых соединены линиями.
Слайд 10
План:
Выяснить признаки фигуры, которую можно нарисовать;
Найти начальную точку;
Нарисовать
всю фигуру
Слайд 11 Не отрывая карандаша от бумаги и не проводя
по одной линии дважды, начертить “открытый конверт”:
Слайд 12
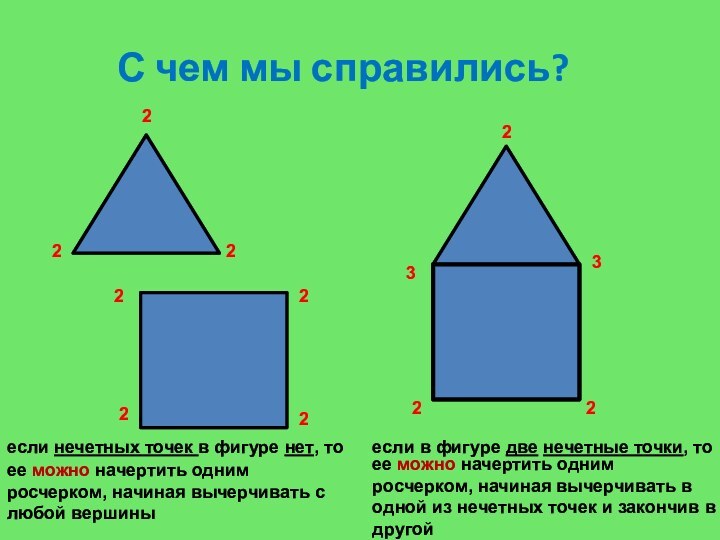
С чем мы справились?
3
3
2
2
2
2
2
2
2
2
2
2
если нечетных точек в фигуре
нет, то
ее можно начертить одним росчерком, начиная вычерчивать
с любой вершиныесли в фигуре две нечетные точки, то
ее можно начертить одним росчерком, начиная вычерчивать в одной из нечетных точек и закончив в другой
Слайд 13 Не отрывая карандаша от бумаги и не проводя
по одной линии дважды, начертить “открытый конверт”:
2
4
4
4
3
3
Слайд 14
Выводы:
1. если нечетных точек в фигуре нет, то
ее можно начертить одним росчерком, начиная вычерчивать с любой
вершины.2. если в фигуре две нечетные точки, то ее можно начертить одним росчерком, начиная вычерчивать в одной из нечетных точек и закончив в другой.
3. если в фигуре больше двух нечетных точек, то ?
Слайд 15 Не отрывая карандаша от бумаги и не проводя
по одной линии дважды, начертить “закрытый конверт”:
3
3
3
3
4
Слайд 16
Выводы:
1. если нечетных точек в фигуре нет, то
ее можно начертить одним росчерком, начиная вычерчивать с любой
вершины.2. если в фигуре две нечетные точки, то ее можно начертить одним росчерком, начиная вычерчивать в одной из нечетных точек и закончив в другой.
3. если в фигуре больше двух нечетных точек, то ее нельзя вычертить одним росчерком.
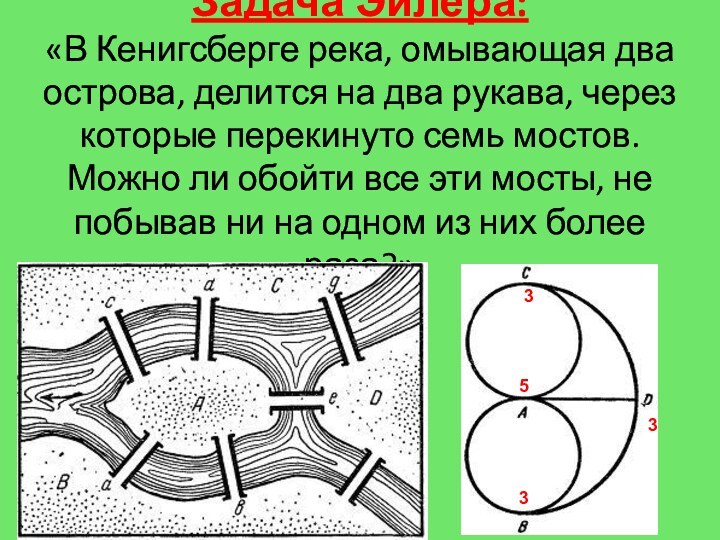
Слайд 20 Задача Эйлера: «В Кенигсберге река, омывающая два острова, делится
на два рукава, через которые перекинуто семь мостов. Можно
ли обойти все эти мосты, не побывав ни на одном из них более раза?»3
3
3
5