Презентация на тему Свойства функции

Содержание

2. Функция y=f(x), x∈X называется чётной, если для
3. Функция y=f(x), x∈X называется нечётной, если для
4. Фунмножестве кцию у=f(x) называют возрастающей на Х⊂
5. Функцию у=f(x) называют убывающей на множестве Х⊂
6. Функция у=f(x) называется ограниченной снизу на множестве
7. Функция у=f(x) называется ограниченной сверху на множестве
8. Число m называют наименьшим значением функции у=f(x)
9. Число М называют наибольшим значением функции у=f(x)
10. Точку х0 называют точкой максимума функции у=f(x),
11. Точки максимума и минимума объединяют общим названием – точки экстремума
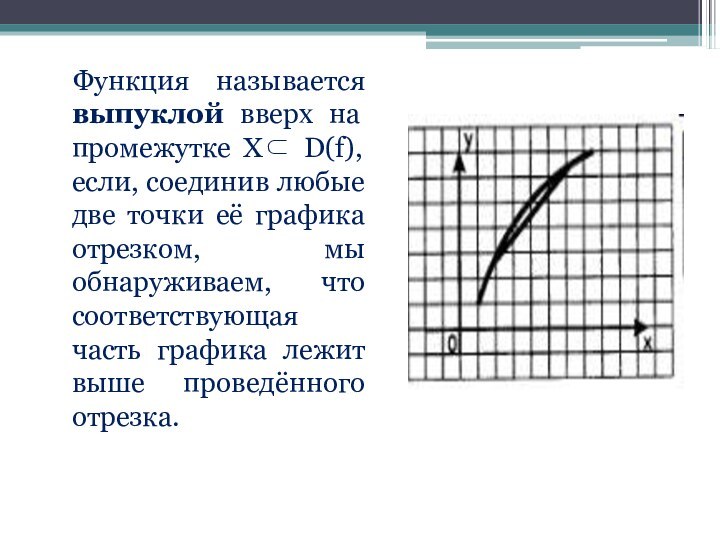
12. Функция называется выпуклой вниз на промежутке Х⊂
13. Скачать презентацию
14. Похожие презентации

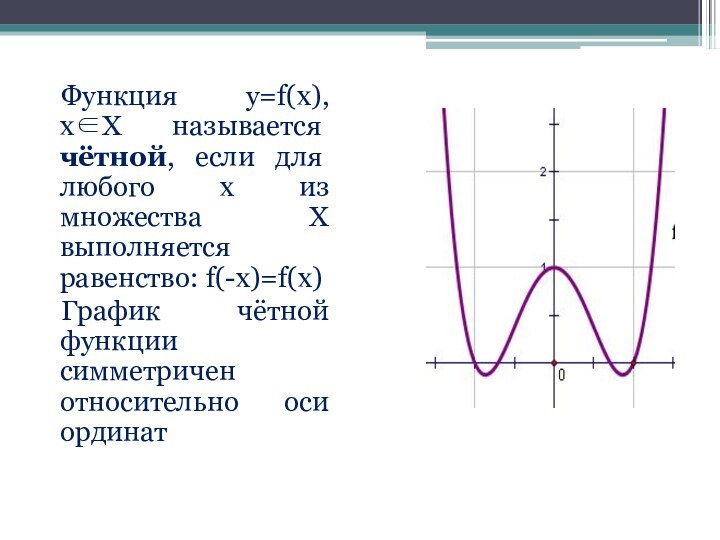
Функция y=f(x), x∈X называется чётной, если для любого х из множества Х выполняется равенство: f(-x)=f(x)График чётной функции симметричен относительно оси ординат

Функция y=f(x), x∈X называется нечётной, если для любого х из множества Х

Фунмножестве кцию у=f(x) называют возрастающей на Х⊂ D(f), если для любых точек

Функцию у=f(x) называют убывающей на множестве Х⊂ D(f), если для любых точек

Функция у=f(x) называется ограниченной снизу на множестве Х⊂ D(f), если все значения

Функция у=f(x) называется ограниченной сверху на множестве Х⊂ D(f), если все значения

Число m называют наименьшим значением функции у=f(x) на множестве Х⊂ D(f), если:1)

Число М называют наибольшим значением функции у=f(x) на множестве Х⊂ D(f), если:1)

Точку х0 называют точкой максимума функции у=f(x), если у этой точки существует

Точки максимума и минимума объединяют общим названием – точки экстремума

Функция называется выпуклой вниз на промежутке Х⊂ D(f), если, соединив любые две

Функция называется выпуклой вверх на промежутке Х⊂ D(f), если, соединив любые две

Слайды презентации

Слайд 2 Функция y=f(x), x∈X называется чётной, если для любого

Функция y=f(x), x∈X называется чётной, если для любого х из множества

х из множества Х выполняется равенство: f(-x)=f(x)
График чётной функции

симметричен относительно оси ординат

Слайд 3 Функция y=f(x), x∈X называется нечётной, если для любого

Функция y=f(x), x∈X называется нечётной, если для любого х из множества

х из множества Х выполняется равенство: f(-x)= -f(x)
График нечётной

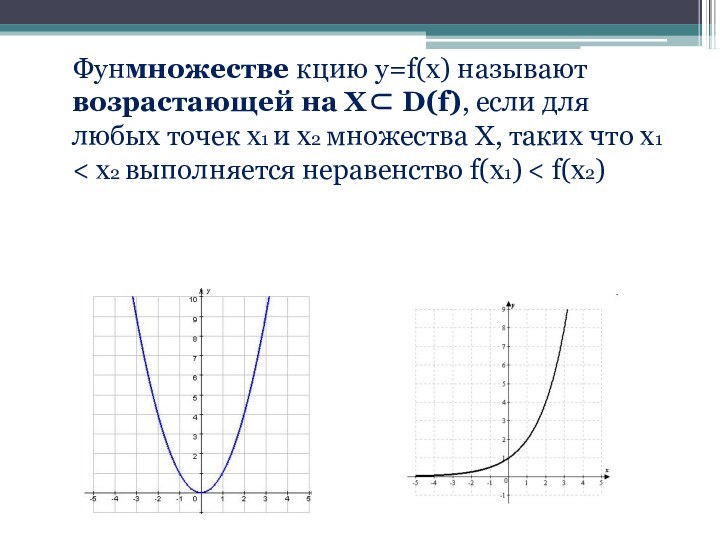
функции симметричен относительно начала координат

Слайд 4 Фунмножестве кцию у=f(x) называют возрастающей на Х⊂ D(f),

Фунмножестве кцию у=f(x) называют возрастающей на Х⊂ D(f), если для любых

если для любых точек х1 и х2 множества Х,

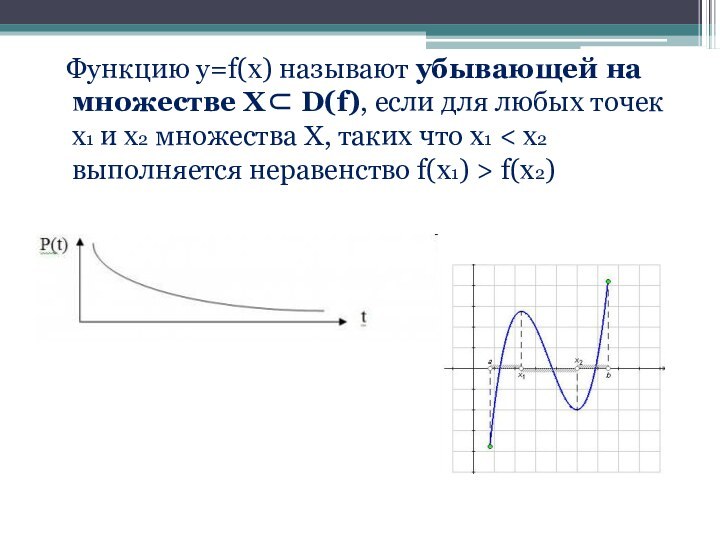
таких что х1 < х2 выполняется неравенство f(х1) < f(х2)

Слайд 5 Функцию у=f(x) называют убывающей на множестве Х⊂ D(f),

Функцию у=f(x) называют убывающей на множестве Х⊂ D(f), если для любых

если для любых точек х1 и х2 множества Х,

таких что х1 < х2 выполняется неравенство f(х1) > f(х2)

Слайд 6 Функция у=f(x) называется ограниченной снизу на множестве
Х⊂

Функция у=f(x) называется ограниченной снизу на множестве Х⊂ D(f), если все

D(f), если все значения этой функции на множестве Х

больше некоторого числа. Иными словами, если существует такое число m, что для любого значения х∈Х выполняется неравенство f(x)>m

Слайд 7 Функция у=f(x) называется ограниченной сверху на множестве Х⊂

Функция у=f(x) называется ограниченной сверху на множестве Х⊂ D(f), если все

D(f), если все значения этой функции на множестве Х

меньше некоторого числа. Иными словами, если существует такое число М, что для любого значения х∈Х выполняется неравенство f(x)

Слайд 8 Число m называют наименьшим значением функции у=f(x) на

Число m называют наименьшим значением функции у=f(x) на множестве Х⊂ D(f),

множестве Х⊂ D(f), если:
1) Во множестве Х существует такая

точка х0, что f(x0)= m;
2) Для любого значения х из множества Х выполняется неравенство: f(x)≥ f(x0).

Слайд 9 Число М называют наибольшим значением функции у=f(x) на

Число М называют наибольшим значением функции у=f(x) на множестве Х⊂ D(f),

множестве Х⊂ D(f), если:
1) Во множестве Х существует такая

точка х0, что f(x0)= М;
2) Для любого значения х из множества Х выполняется неравенство: f(x)≤ f(x0).

Слайд 10 Точку х0 называют точкой максимума функции у=f(x), если

Точку х0 называют точкой максимума функции у=f(x), если у этой точки

у этой точки существует окрестность для всех точек которой

(кроме самой точки х0) выполняется неравенство f(x)Точку х0 называют точкой минимума функции у=f(x), если у этой точки существует окрестность для всех точек которой (кроме самой точки х0) выполняется неравенство f(x)>f(х0).