Слайд 2
Исследование функций и построение графиков с помощью производной
Слайд 3
«…нет ни одной области в математике, которая когда-либо
не окажется применимой к явлениям действительного мира…»
Н.И. Лобачевский
Скажи мне, и я забуду.
Покажи мне, и я запомню.
Дай мне действовать самому,
И я научусь.
Конфуций
Слайд 4
Цели урока:
⮚ Образовательные.
Формировать:
- навыки прикладного
использования аппарата производной;
- выявить уровень овладения учащимися комплексом
знаний и умений по исследованию функции и ликвидировать пробелы в знаниях в соответствии с требованиями к математической подготовке учащихся.
⮚ Развивающие.
Развивать:
- способности к самостоятельному планированию и организации работы
- навыки коррекции собственной деятельности через применение информационных технологий;
- умение обобщать, абстрагировать и конкретизировать знания при исследовании функции.
⮚ Воспитательные.
Воспитывать:
- познавательный интерес к математике;
- информационную культуру и культуру общения;
- самостоятельность, способность к коллективной работе.
Слайд 5
I этап. Актуализация ЗУН, необходимых для
творческого применения знаний
Необходимое условие возрастания и убывания функции
Достаточное
условие возрастания и убывания функции
Необходимое условие экстремума. (теорема Ферма)
Признак максимума функции.
Признак минимума функции.
Достаточные условия выпуклости и вогнутости графика функции
Слайд 6
Необходимое условие возрастания и убывания функции
Т е о
р е м а.
Если дифференцируемая функция f(x), х∈(а;b), возрастает (убывает) на (а;b), то f `(x) ≥ 0 (f `(x) ≤ 0) для любого х из интервала (а;b).
Слайд 7
Достаточные условия возрастания и убывания функции
Теорема Лагранжа.
Если
функция f(x), х∈[а;b], непрерывна на отрезке [а;b] и дифференцируема
на интервале (а;b), то найдётся точка с∈(а;b) такая, что имеет место формула
f(a) – f(b) = f `(c)(b – a)
Слайд 8
Достаточное условие возрастания функции
Теорема.
Если функция f имеет неотрицательную производную в каждой точке интервала (а;b), то функция f возрастает на интервале (а;b).
Слайд 9
Достаточное условие убывания функции
Теорема.
Если функция имеет неположительную производную в каждой точке интервала (а;b), то функция f убывает на интервале (а;b).
Слайд 10
α
α
Функция возрастает
α < 900
tg
α > 0
f `(x) > 0
Функция убывает
α > 900
tg α < 0
f `(x) < 0
Слайд 11
Правило нахождения интервалов монотонности
1) Вычисляем производную f
`(x) данной функции f(x), а затем находим точки, в
которых f `(x) равна нулю или не существует. Эти точки называются критическими для функции f(x)
Слайд 12
Правило нахождения интервалов монотонности
2) Критическими точками область определения
функции f(x) разбивается на интервалы, на каждом из которых
производная f `(x) сохраняет свой знак. Эти интервалы будут интервалами монотонности.
Слайд 13
Правило нахождения интервалов монотонности
3) Определим знак
f `(x) на каждом
из найденных интервалов. Если на рассматриваемом интервале f `(x) ≥ 0, то на этом интервале f(x) возрастает, если же f `(x) ≤ 0, то на таком интервале f(x) убывает.
Слайд 14
Исследование экстремумов функции
Необходимое условие экстремума.
(теорема Ферма)
Если точка х0 является точкой экстремума функции f
и в этой точке существует производная f `(x), то она равна нулю:
f `(x) = 0.
Слайд 15
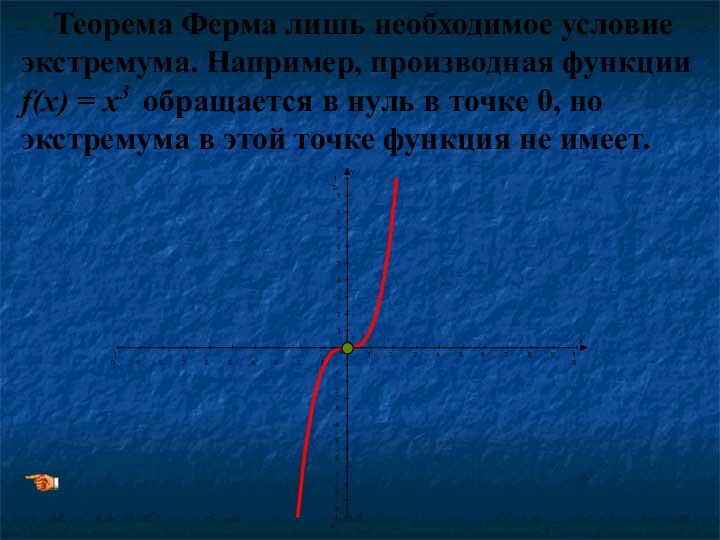
Теорема Ферма лишь необходимое условие экстремума.
Например, производная функции f(x) = x3 обращается в нуль
в точке 0, но экстремума в этой точке функция не имеет.
0
Слайд 16
Достаточные условия существования экстремума в точке
Признак максимума функции.
Если функция f непрерывна в точке х0, а
f `(x) > 0 на интервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f.
построение
Слайд 17
Достаточные условия существования экстремума в точке
Признак минимума функции.
Если функция f непрерывна в точке х0, f `(x)
< 0 на интервале
(а; х0) и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f
X
Y
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
0
построение
Слайд 18
Достаточные условия выпуклости и вогнутости графика функции
Т е
о р е м а. Пусть функция f(x), х∈(а;b),
имеет первую и вторую производные. Тогда, если f ``(x) < 0 для всех х∈(а;b), то на интервале (а;b) график функции f(x) выпуклый вверх, если же f ``(x) > 0 для всех х∈(а;b), то график функции f(x) выпуклый вниз на (а;b).
Слайд 19
α1
α2
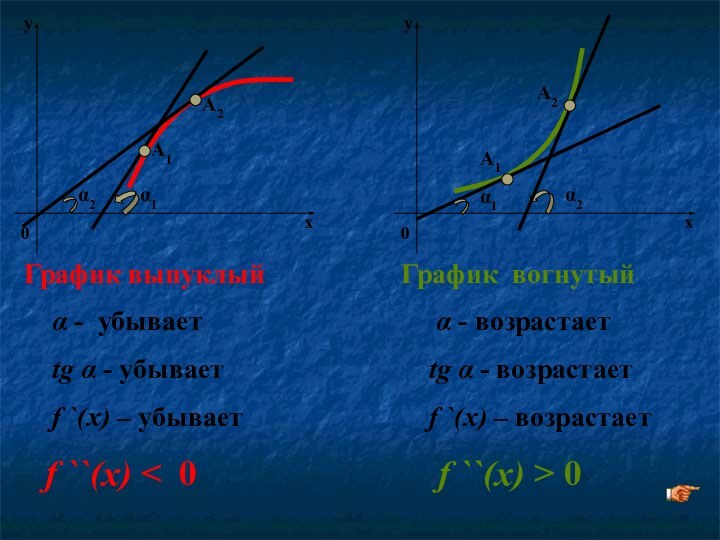
График выпуклый
α - убывает
tg
α - убывает
f `(x) – убывает
f ``(x) < 0
График вогнутый
α - возрастает
tg α - возрастает
f `(x) – возрастает
f ``(x) > 0
α1
α2
A1
A2
A1
A2
Слайд 20
Точки перегиба
Найти критические точки функции по второй производной.
Исследовать
знак второй производной в некоторой окрестности критический точки.
Если f ``(х) меняет свой знак при переходе аргумента через критическую точку х0, то (х0; f(х0)) - точка перегиба графика данной функции
Слайд 21
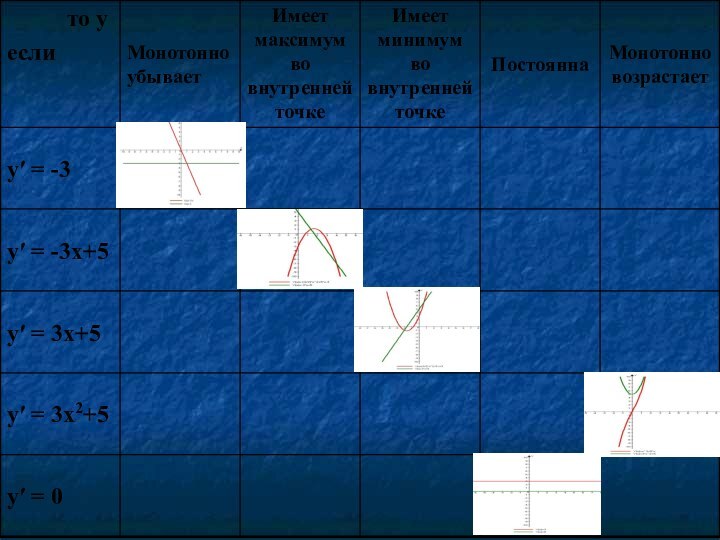
Заполните таблицу
Задание для всех учащихся.
II этап. Обобщение и
систематизация знаний и способов деятельности
Слайд 23
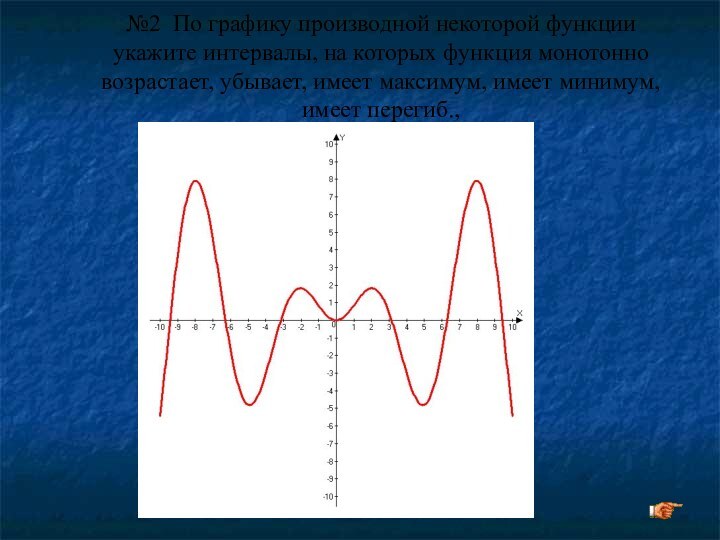
№2 По графику производной некоторой функции укажите интервалы,
на которых функция монотонно возрастает, убывает, имеет максимум, имеет
минимум, имеет перегиб.,
Слайд 24
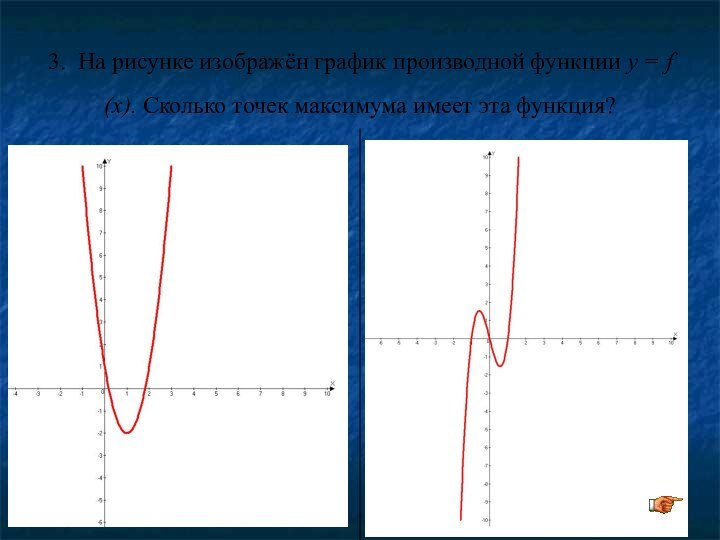
3. На рисунке изображён график производной функции y
= f (x). Сколько точек максимума имеет эта функция?
Слайд 25
у = x3 – 3x2 + x
+ 5
у = (x2 – 1)2
Ответы
Слайд 26
III этап. Усвоение образца комплексного применения ЗУН.
Практическая работа
с применением электронного учебного пособия «Математика – практикум 5-11»
и по индивидуальным заданиям на местах.
За компьютер сначала рассаживаются 7 учащихся, остальные за парты. По мере выполнения заданий ребята меняются местами.
Слайд 27
Работа на компьютере
Работа на местах
Слайд 28
Работа с ЭУП «Математика – практикум
5-11»
Слайд 30
Работа на компьютере
Работа на местах
Слайд 31
Работа на компьютере
Работа на местах
Слайд 33
Исследовать функцию на выпуклость, вогнутость.
Слайд 34
Мини - исследовательская работа
Выбери задание
1.
3.
5.
2.
4.
6.






![Исследование функций с помощью производной Достаточные условия возрастания и убывания функцииТеорема Лагранжа. Если функция f(x), х∈[а;b], непрерывна](/img/tmb/15/1429976/d7c9d3252439d5a37b240f145bb8fe95-720x.jpg)