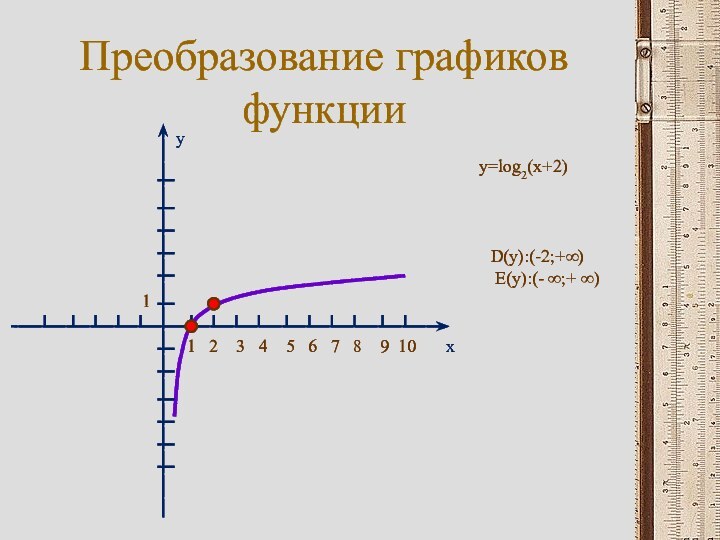
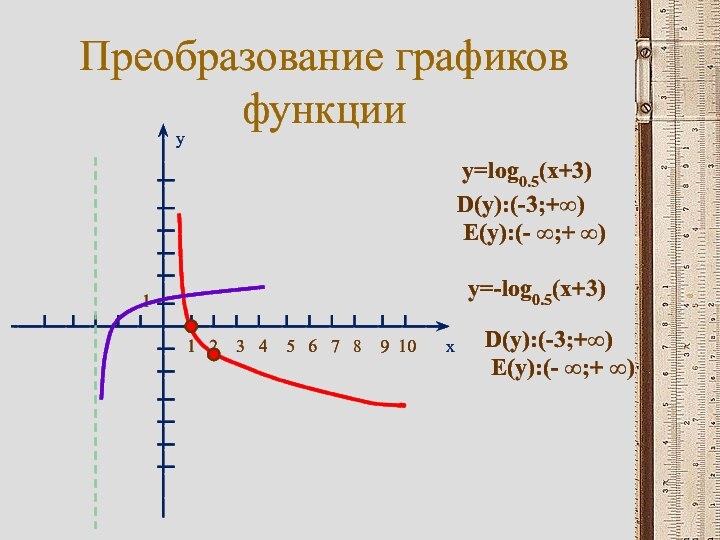
съезда физиков в Одессе. Некоторым
учащимся на дом предлагалось
творческоезадание: число 3, целое и положительное,
изобразить с помощью трех двоек и
математических символов.
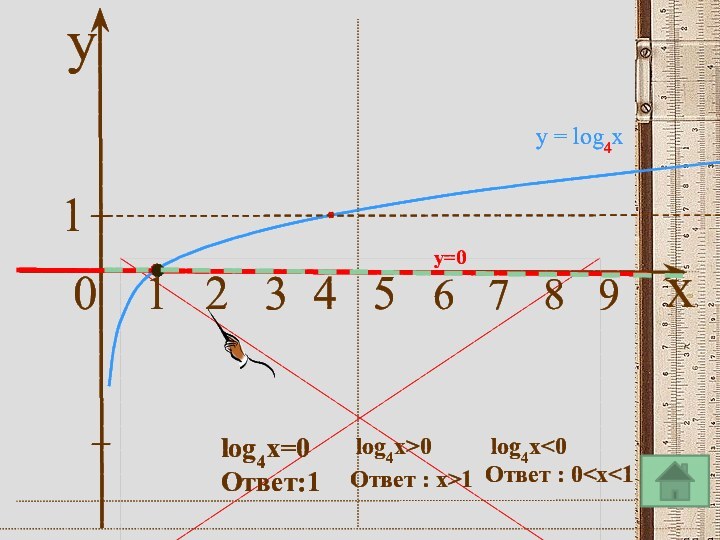
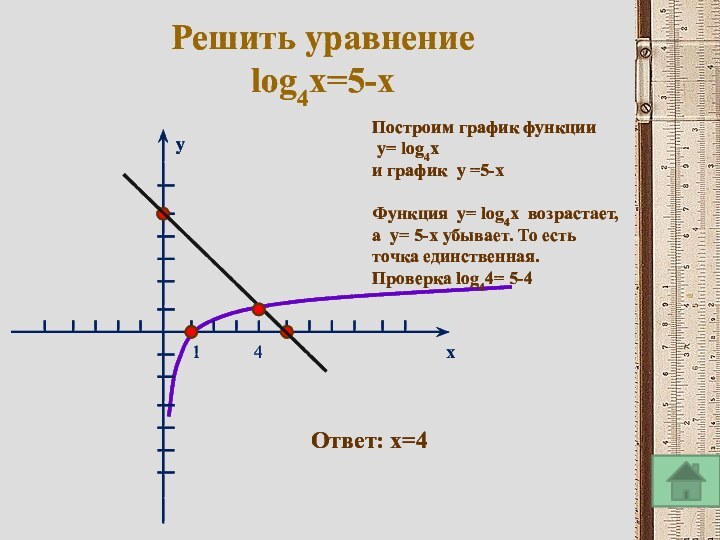
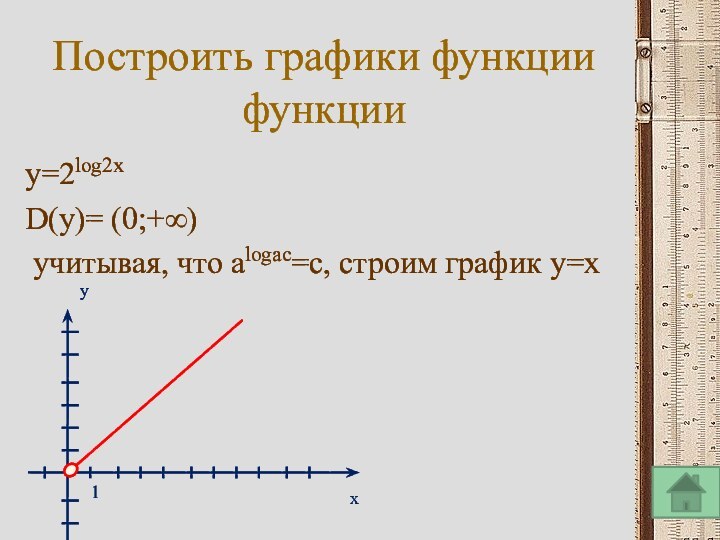
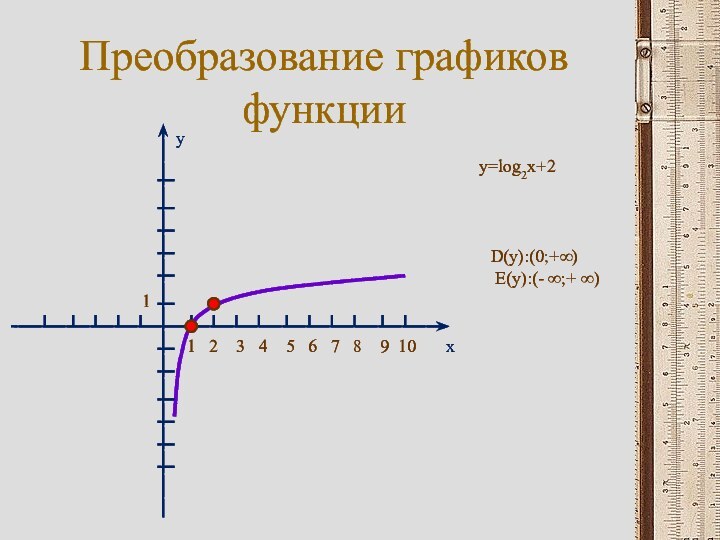
То есть любое целое положительное число можно изобразить с помощью трех двоек и математических символов.





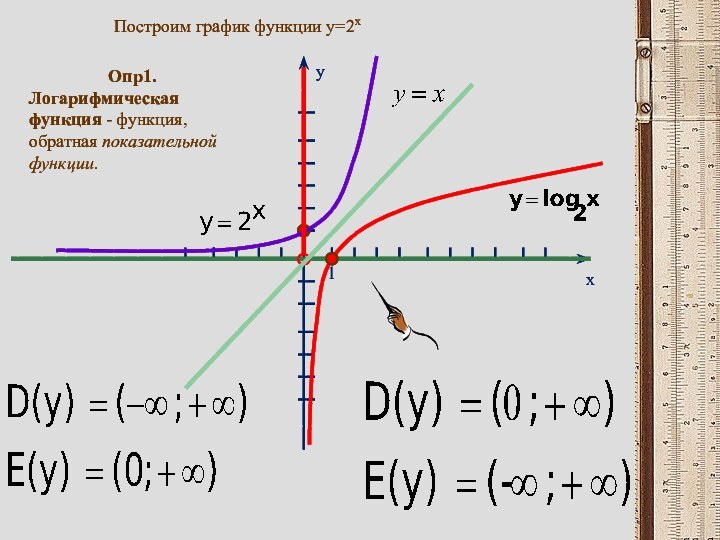
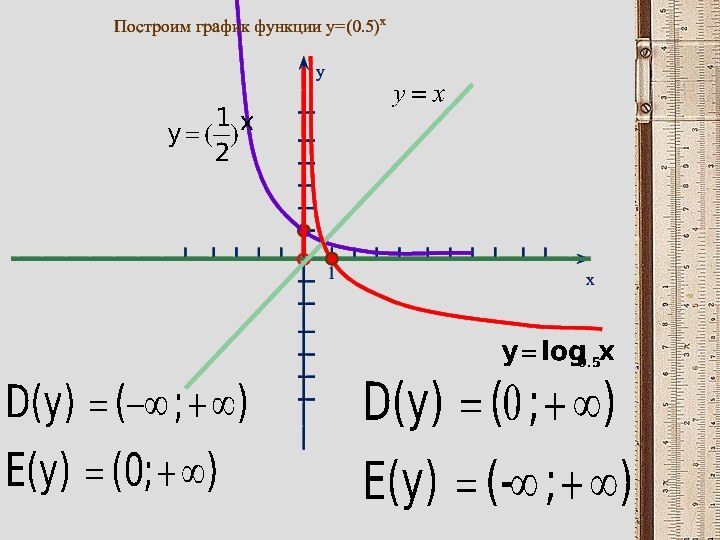




![Логарифмическая функция, её свойства и график Найти наименьшее и набольшее значении функции на заданном промежуткеy=lgx x€ [1;1000]Решение: функция](/img/tmb/11/1078082/7724374bc4eebbaca7ae6c7200c061aa-720x.jpg)