- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математический словарь
Содержание
- 2. СодержаниеАРХИТ ТАРЕНТСКИЙАСИПТОТЫБИССЕКТРИСА ТРЕУГОЛЬНИКАБЕРНУЛЛИ ЯКОБВЕКТОРВЫСОТА ЦИЛИНДРАГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕКЛИНЕЙНЫЕ
- 3. Архит ТарентскийАрхит Тарентский (428-347 г. до н.э.)
- 4. АсимптотыАсимптоты графика функции. Пусть y=f(x)- функция, график
- 5. АсимптотыВертикальная асимптота x=0; ОХУНаклонная асимптота(горизонтальная) у = 0 ОXНаклонная асимптотау=2х
- 6. Биссектриса треугольникаБиссектриса треугольника - отрезок биссектрисы угла
- 7. Бернулли ЯкобБернулли Якоб (1654-1705) - швейцарский математик,
- 8. ВекторВектор. Отрезок, для которого указано, какой из
- 9. ВекторВекторы называются равными, если они сонаправлены и
- 10. Высота цилиндраВысота цилиндра - отрезок перпендикулярной прямой,
- 11. Геометрическое место точекПод этим термином понимается всякое
- 12. Геометрическое место точекГеометрическим местом точек, равноудалённых от
- 13. Геометрическое место точекГеометрическое место точек, удалённых от
- 14. Геометрическое место точекГеометрическим местом точек, удаленных от
- 15. Линейные функции. Функция, заданная формулой y=kx+b, где
- 16. Частные случаи линейной функции: 1. Если
- 17. Линейные функцииЧастные случаи линейной функции: 2.
- 18. Ломанная - геометрическая фигура, состоящая из точек,
- 19. Луч - часть прямой, состоящая из всех
- 20. Острый угол – угол, градусная мера которого
- 21. Остроградский Михаил Васильевич (1801-1861) – выдающийся русский
- 22. Параллелограмм – четырехугольник, у которого противоположные стороны
- 23. Признаки параллелограмма:Если в четырехугольнике две стороны равны
- 24. Параллельные плоскости - плоскости, которые не пересекаются.
- 25. Свойства параллельных плоскостей:Если две параллельные плоскости пересечены
- 26. Параллельные прямые на плоскости. Две прямые на
- 27. Подобие- отображение плоскости или пространства на себя,
- 28. Подобные фигуры Ф1 и Ф2, если существует
- 29. Признаки подобия треугольников:Первый признак подобия: если два
- 30. Теорема – математическое предложение, правильность или истинность
- 31. Теорема косинусов: квадрат стороны треугольника равен сумме
- 32. Теорема о биссектрисе равнобедренного треугольника: в равнобедренном
- 33. Теорема о средней линии трапеции: средняя линяя
- 34. Теорема о средней линии треугольника: средняя линия
- 35. Теорема Пифагора:квадрат гипотенузы равен сумме квадратов катетов,
- 36. Теорема синусов: стороны пропорциональны синусам противолежащих углов, т.е.Теорема синусов
- 37. Теорема Фалеса: если параллельные прямые, пересекающие стороны
- 38. Точка - одно из основных неопределяемых понятий
- 39. Торричелли Эванджелиста (1608-1647)- известный итальянский ученный, ученик
- 40. Ат-Туси (1201-1274) - азербайджанский астроном и математик,
- 41. Угол - гомерическая фигура, состоящая из двух
- 42. Если угол равен половине развернутого угла,
- 43. Текстовые задачи на составление уравнений.Большая часть текстовых
- 44. Задача1. Катер прошел расстояние между пристанями по
- 45. Задачи на движениеЗадача2. Из пункта А в
- 46. Задача1. Имеется руда из двух пластов с
- 47. Задача1. Найти площадь прямоугольника, длина которого в
- 48. Скачать презентацию
- 49. Похожие презентации








































Слайд 2
Содержание
АРХИТ ТАРЕНТСКИЙ
АСИПТОТЫ
БИССЕКТРИСА ТРЕУГОЛЬНИКА
БЕРНУЛЛИ ЯКОБ
ВЕКТОР
ВЫСОТА ЦИЛИНДРА
ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК
ЛИНЕЙНЫЕ ФУНКЦИИ
ЛОМАННАЯ
ЛУЧ
ОСТРЫЙ
УГОЛ
СОСТАВЛЕНИЕ УРАВНЕНИЙ
Слайд 3
Архит Тарентский
Архит Тарентский (428-347 г. до н.э.) -
знаменитый древнегреческий математик , астроном и государственный деятель. Он
обладал большим талантом и трудолюбием. Его труды оказали влияние на Платона и Евклида. Архит был неутомим: он доказывал теоремы и строил деревянного летающего голубя, решал задачу об удвоении куба и мастерил детскую трещотку.
Слайд 4
Асимптоты
Асимптоты графика функции. Пусть y=f(x)- функция, график которой
имеет бесконечную ветвь, т.е. ветвь, имеющую точки, принадлежащие графику
функции и находящиеся сколь угодно далеко от начала координат.Асимптотой графика функции y=f(x) называют прямую, обладающую тем свойством, что расстояние от точки (x;f(x)) до этой прямой стремится к нулю при движении этой точки вдоль ветви к бесконечности.
Асимптоты бывают двух видов: вертикальные и наклонные (в частности, горизонтальные).
Рассмотрим графики функций, имеющие вертикальные асимптоты:
Слайд 5
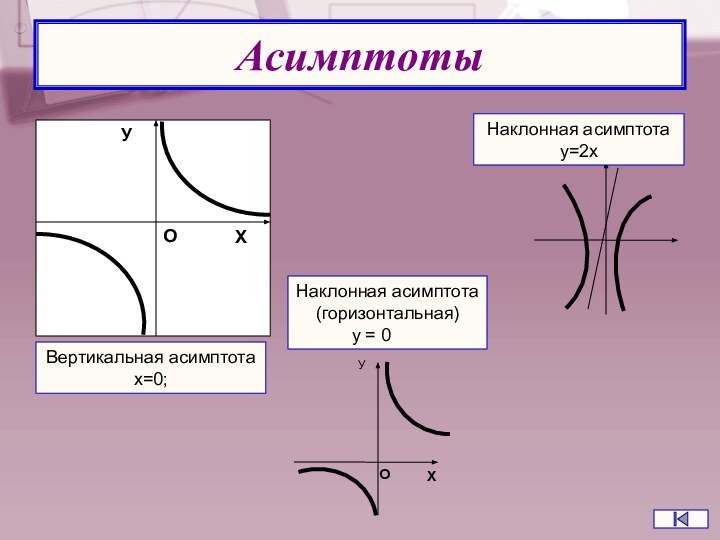
Асимптоты
Вертикальная асимптота
x=0;
О
Х
У
Наклонная асимптота
(горизонтальная)
у = 0
О
X
Наклонная асимптота
у=2х
Слайд 6
Биссектриса треугольника
Биссектриса треугольника - отрезок биссектрисы угла треугольника,
соединяющий вершину треугольника с точкой противоположной стороны. Точка пересечения
биссектрис треугольника является центром вписанной в него окружности.Отрезки АА1, ВВ1 и СС1 – биссектрисы ∆ABC; O- вписанный центр окружности.
Биссектриса AD треугольника ABC делит сторону BC на отрезки BD и DC, пропорциональные сторонам AB и AC.
Биссектриса AD треугольника ABC делит его на два треугольника ABD и ACD, площади которых пропорциональны длинам сторон AB и AC.
А
А1
В
В1
С
С1
А
В
С
D
Отрезок AD- биссектриса
Слайд 7
Бернулли Якоб
Бернулли Якоб (1654-1705) - швейцарский математик, один
их ярких представителей семьи ученых Бернулли. Сначала Бернулли занимался
изучением теологии, позднее увлекся математикой. Был профессором математики Базельского университета. Якоб Бернулли сформулировал и частично решил ряд важных задач математики и механики и механики. В книге «Арифметические приложения о бесконечных радах и их конечных суммах», которая была первым учебником по теории рядов, он доказал расходимость гармоничного ряда. Решил также ряд задач комбинаторики теории вероятностей, оказал большое влияние на приложение теории вероятностей к практике. Его учениками были брат Иоганн Бернулли, племянник Николай Бернулли.
Слайд 8
Вектор
Вектор. Отрезок, для которого указано, какой из его
концов считается началом, а какой- концом, называется направленным отрезком,
или вектором. Обозначается , длина этого отрезка называется длиной вектора. Обозначается .Вектор, длина которого равна нулю, называется нулевым. Начало нулевого вектора совпадает с его концом. Любую точку плоскости можно считать нулевым вектором.Противоположными векторами называются векторы, которые имеют равные длины и противоположные направления.
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, или на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.
Коллинеарные векторы, если они одинаково направлены, называются сонаправленными, если противоположно направлены, называются противоположно направленными. Обозначаются
Слайд 9
Вектор
Векторы называются равными, если они сонаправлены и имеют
равные длины если
и .Три ненулевых вектора называются комплпантарными, если лучи, задающие их направление, принадлежат прямым, параллельным некоторой плоскости.
Над векторами можно проводить следующие операции: сложение векторов, вычитание векторов, умножение вектора на число, скалярное произведение векторов.
Суммой векторов называется вектор
Законы сложения векторов:
Переместительный закон
Сочетательный закон
Слайд 10
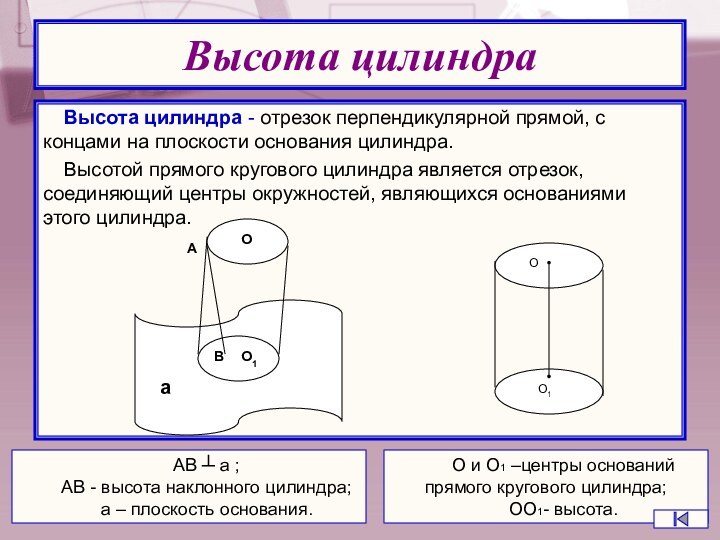
Высота цилиндра
Высота цилиндра - отрезок перпендикулярной прямой, с
концами на плоскости основания цилиндра.
Высотой прямого кругового цилиндра является
отрезок, соединяющий центры окружностей, являющихся основаниями этого цилиндра.АВ ┴ а ;
АВ - высота наклонного цилиндра;
а – плоскость основания.
О и О1 –центры оснований прямого кругового цилиндра;
ОО1- высота.
Слайд 11
Геометрическое место точек
Под этим термином понимается всякое множество
или совокупность точек, обладающим каким – то общим для
них свойством, но неприсущим остальным точкам, не принадлежащим данному или совокупности. В последнее время этот термин стал реже употребляться. Примеры.Геометрическим местом точек, равноудаленных от двух данных точек А и В, является прямая, перпендикулярная отрезку АВ и проходящая через его середину.
Даны точки А и В, прямая l перпендикулярна отрезку АВ, причём АО = ОВ. Прямая l – геометрическое место точек, равноудалённых от точек. А и В на плоскости.
Если рассматривать точки А и В а пространстве,
то геометрическим местом точек, равноудалённых
от точек А и В, будет плоскость, проходящая
через середину отрезка АВ и перпендикулярно
прямой АВ.
Слайд 12
Геометрическое место точек
Геометрическим местом точек, равноудалённых от сторон
угла, является биссектриса этого угла.
Дан угол АВС, BD –
биссектриса ∟АСВ. Луч BD – геометрическое место точек, равноудалённых от лучей ВА и ВС, т.е. ЕМ┴ВС и ЕМ = ЕN.
Слайд 13
Геометрическое место точек
Геометрическое место точек, удалённых от данной
прямой на расстоянии d, представляет собой пару прямых, параллельных
данной и отстоящих от неё на расстоянии d.Дана прямая а, прямые l1 и l2 параллельны прямой а и находятся на расстоянии d от прямой а, т.е. l1 ║ l2 и ОА┴l1; ОВ ┴ l2 и ОА=ОВ=d.Прямые l1 и l2 являются геометрическим местом точек, равноудаленных от прямой, а на плоскости.
Если рассматривать прямую а в пространстве, то геометрическим местом точек, равноудаленных от прямой а являются две плоскости, параллельных прямой, а и находящиеся от нее на одном и тои же расстоянии. Эти плоскости являются параллельными плоскостями.
О
А
В
l2
a
l1
Слайд 14
Геометрическое место точек
Геометрическим местом точек, удаленных от данной
точки O на расстояние R, является окружность с центром
в точке O и радиусом R.Окружность является геометрическим местом точек, равноудаленных от точки на данное расстояние, на плоскости.
Если рассматривать точку O в пространстве, то геометрическим местом точек, равноудаленных от точки O на расстояние R, является сфера с центром в точке O и радиусом R: ОА=ОВ=R.
А
R
О
Слайд 15 Линейные функции. Функция, заданная формулой y=kx+b, где k
и b – некоторые действительные числа, называется линейной.
Свойства
линейной функции (при условии )Областью определения линейной функции является множество всех действительных чисел.
Множество значений линейной функции при множество всех действительных чисел.
При k функция возрастает, при функция убывает.
Линейная функция не является ни четной, ни нечетной.
Графиком линейной функции является прямая. Для построения графика линейной функции достаточно определить
координаты двух точек графика и через них
провести прямую.
Линейные функции
y=kx+b
У
X
В
О
а
Удобно брать точки, у которых либо абсцисса, либо ордината равны нулю:
Число k называется угловым коэффициентом прямой. Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси, Ох: k=tg a.
Слайд 16
Частные случаи линейной функции:
1. Если b=0,
то линейная функция задается формулой y=kx. Такая функция называется
прямой пропорциональностью. Графиком прямой пропорциональности является прямая, проходящая через начало координат.Линейные функции
y=kx+b
У
Х
О
Слайд 17
Линейные функции
Частные случаи линейной функции:
2. Если
, то линейная функция задается формулой y=b. Такая функция
называется постоянной. Графиком постоянной функции является прямая, параллельная оси Ох. Если k=0 и b=0, то график постоянной функции совпадает с осью Ох.
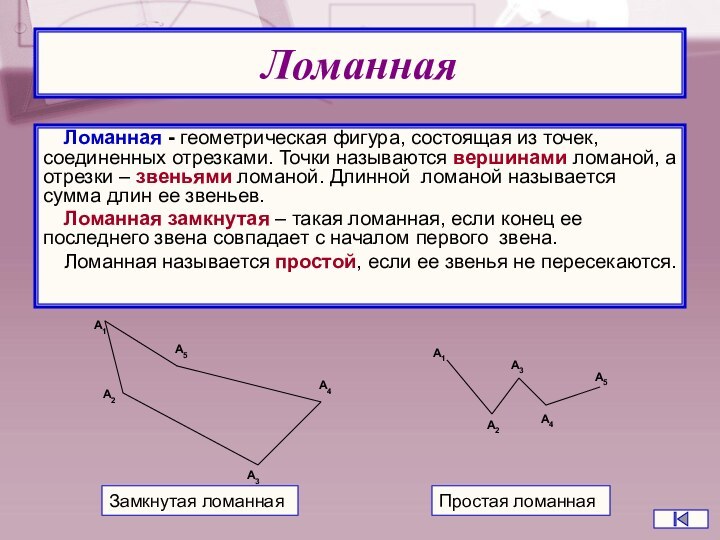
Слайд 18 Ломанная - геометрическая фигура, состоящая из точек, соединенных
отрезками. Точки называются вершинами ломаной, а отрезки – звеньями
ломаной. Длинной ломаной называется сумма длин ее звеньев.Ломанная замкнутая – такая ломанная, если конец ее последнего звена совпадает с началом первого звена.
Ломанная называется простой, если ее звенья не пересекаются.
Ломанная
Замкнутая ломанная
Простая ломанная
А1
А2
А3
А4
А5
Слайд 19 Луч - часть прямой, состоящая из всех точек
этой прямой, лежащих по одну сторону от данной точки.
Эта точка называется началом луча. Точка делит прямую на два луча, поэтому луч иногда называют полупрямой. Различные полупрямые одной и той же прямой с общим началом называют дополнительными полупрямыми или дополнительными лучами. Обозначение: луч ОА или , где О – начало луча, можно обозначать луч а.Луч
О
А
а
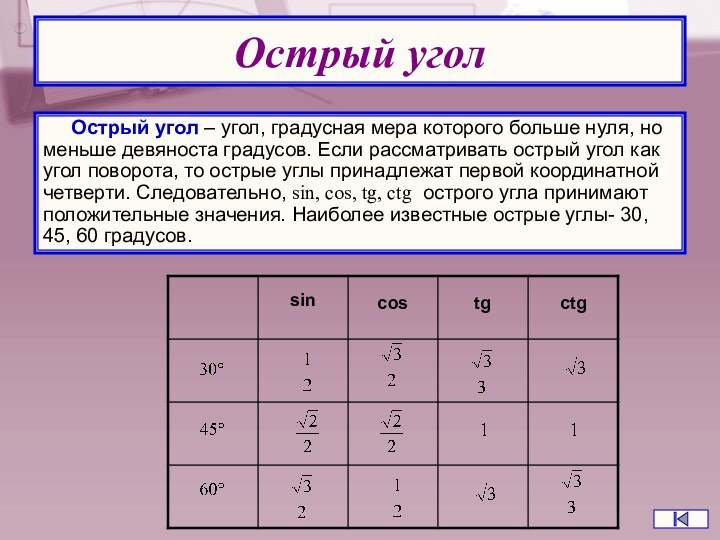
Слайд 20 Острый угол – угол, градусная мера которого больше
нуля, но меньше девяноста градусов. Если рассматривать острый угол
как угол поворота, то острые углы принадлежат первой координатной четверти. Следовательно, sin, cos, tg, ctg острого угла принимают положительные значения. Наиболее известные острые углы- 30, 45, 60 градусов.Острый угол
Слайд 21 Остроградский Михаил Васильевич (1801-1861) – выдающийся русский математик,
был членом многих академий наук. Занимался математическим анализом, алгеброй,
теорией чисел, прикладным науками. Он составил учебники по высшей и элементарной математике, вел большую педагогическую деятельность.Родился Остроградский в семье помещика Полтавской губернии. С ранних лет проявил математические способности, в 16 лет поступил на физико-математичский факультет Харьковского университета. Но не смог получить диплом этого университета, так как отказывался посещать лекции по богословию. Поэтому продолжил образование в Париже, где обратил на себя внимание великих математиков того времени. М.И.был одним из тех ученых, которые прославили русскую науку того времени.
Остроградский Михаил Васильевич
Слайд 22 Параллелограмм – четырехугольник, у которого противоположные стороны попарно
параллельны.
Свойства параллелограмма:
a. Противоположные стороны и противоположные углы параллелограмма равны.
b.
Диагональ параллелограмма делит его на два равных треугольника.c. Диагонали параллелограмма делятся точкой пересечения пополам, эта точка является центром симметрии параллелограмма.
d. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: , где d1 и d2 –диагонали, а и b – стороны параллелограмма.
Параллелограмм
Слайд 23
Признаки параллелограмма:
Если в четырехугольнике две стороны равны и
параллельны, то этот четырехугольник – параллелограмм.
Если в четырехугольнике
противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Параллелограмм
BK и BM - высоты
параллелограмма
ABCD, AD и CD –
основания.
Высотой параллелограмма называется перпендикуляр, опущенный из вершины параллелограмма на прямую, содержащую противоположную сторону.
Площадь параллелограмма можно найти по следующим формулам:
, где а - основание, ha - высота, проведенная к основанию.
, где а и b - соседние стороны параллелограмма, α – угол между а и b.
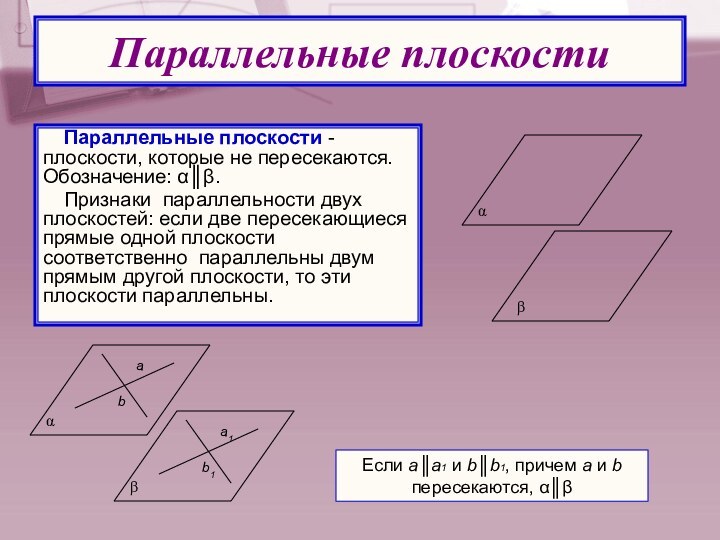
Слайд 24 Параллельные плоскости - плоскости, которые не пересекаются. Обозначение:
α║β.
Признаки параллельности двух плоскостей: если две пересекающиеся прямые
одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.Параллельные плоскости
Если а║а1 и b║b1, причем а и b пересекаются, α║β
Слайд 25
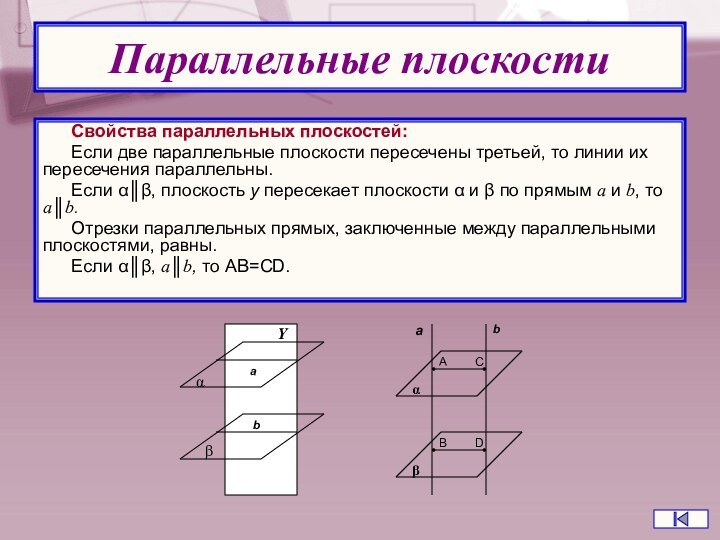
Свойства параллельных плоскостей:
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.
Если α║β, плоскость у пересекает
плоскости α и β по прямым а и b, то а║b.Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Если α║β, а║b, то AB=CD.
Параллельные плоскости
β
Y
b
b
а
Слайд 26 Параллельные прямые на плоскости. Две прямые на плоскости
не имеют общих точек, то они называются параллельными прямыми.
Обозначаются: а║b.Отрезки, лежащие на параллельных прямых, называются параллельными отрезками.
Параллельные прямые на плоскости
Признаки параллельности двух прямых:
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей соответственные углы, то прямые параллельны.
Если при пересечении двух прямых сумма односторонних углов равна 180 градусам, то прямые параллельны.
Слайд 27 Подобие- отображение плоскости или пространства на себя, при
котором расстояние между точками изменяется в одном и том
же отношении . Другими словами, расстояние между точками или увеличивается, или уменьшается в k раз. Число k называется, коэффициентом подобия является подобия. Если k=1, то подобие является движением. Гомотетия является преобразованием подобия., но не всякое подобие является гомотетией.Подобие
Свойства подобия:
При преобразовании подобия прямые переходят в прямые, отрезки в отрезки, лучи в лучи, плоскости в плоскости, углы в равные им углы.
При преобразовании подобия три точки А, В, С, лежащие на одной прямой, переходят в точки А1, В1, С1, лежащие на одной прямой в том же порядке, что и точки ∆ АВС подобен треугольникам ∆ А1, В1, С1 и ∆ А2, В2, С2, но гомотетичен только ∆ А1, В1, С1. ∆ А1, В1, С1 и ∆ А2, В2, С2 являются подобными, но не являются гомотетичными.
Слайд 28 Подобные фигуры Ф1 и Ф2, если существует преобразование
подобия, переводящее одну фигуру в другую. Если фигура Ф1
переходит в фигуру Ф2 при преобразовании подобия с коэффициентом k, то фигура переходит в фигуру Ф1 скоэффициентом .
Особое внимание в школьной программе уделяется подобным треугольникам. Подобные треугольники- треугольники, у которых соответствующие углы равны, а соответствующие стороны пропорциональны.
Обозначение: ∆ АВС~∆ А1 В1С1.
Если треугольники подобны, то отношение площадей равно квадрату коэффициента подобия, т.е. если ∆ АВС~∆ А1 В1С1, то
.
Подобие
Слайд 29
Признаки подобия треугольников:
Первый признак подобия: если два угла
одного треугольника соответственно равны углам другого треугольника, то такие
треугольники подобны.Второй признак подобия: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то треугольники подобны.
Третий признак подобия: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Частные случаи подобия треугольников:
Прямоугольные треугольники подобны, если острый угол одного треугольника равен острому углу другого треугольника.
Прямоугольные треугольники подобны, если гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.
Равнобедренные треугольники подобны, если у них углы между боковыми сторонами равны.
Равнобедренные треугольники подобны, если угол при основании одного треугольника равен углу при основании другого треугольника.
При решении задач удобно использовать такие свойства подобных треугольников:
Средняя линия треугольника отсекает треугольник, подобный данному.
Отношение периметров подобных треугольников рано коэффициенту подобия.
Подобие
Слайд 30 Теорема – математическое предложение, правильность или истинность которого
доказывается с помощью аксиом или других теорем. Классическая теорема
состоит из двух частей из условия и заключения. Условие обыкновенно начинается со слов «если», а заключение - со слова «то».И сейчас существуют теоремы, истинность которых не могут доказать в течении длительного периода времени, например, теорему Ферма о решении некоторого уравнения с тремя переменными в натуральных числах.
Теорема Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е. если x1 и x2– корни уравнения x²+px+q=0 , то x1 + x2=-p и x1x2=q.
Для нахождения корней пользуются теоремой, обратной теореме Виета: если сумма двух чисел равна –p, а произведение равно q, то эти числа являются корнями уравнения x²+px+q=0.
Теорема
Слайд 31 Теорема косинусов: квадрат стороны треугольника равен сумме квадратов
двух других сторон без удвоенного произведения этих сторон на
косинус угла между ними, т.е.a²=b² +c²-2bc cosA;
b²= a²+c²-2аb cosВ;
c²= a²+ b²-2аb cosC.
Теорему косинусов называют обобщенной теоремой Пифагора.
Теорема косинусов
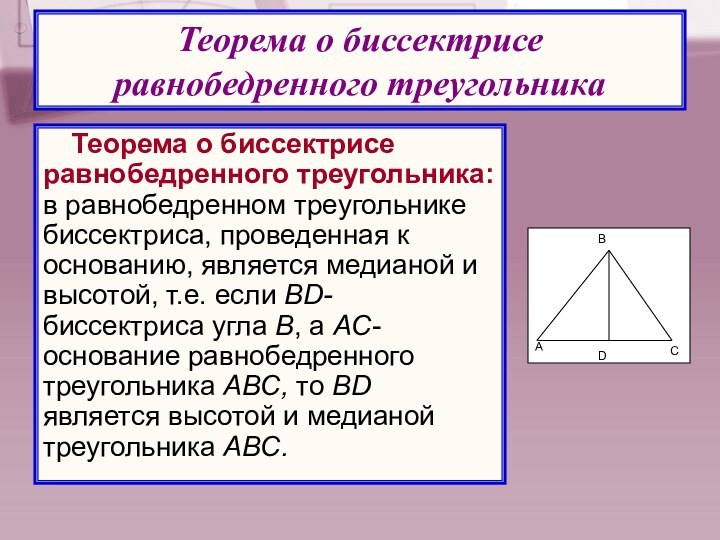
Слайд 32 Теорема о биссектрисе равнобедренного треугольника: в равнобедренном треугольнике
биссектриса, проведенная к основанию, является медианой и высотой, т.е.
если BD- биссектриса угла В, а AC- основание равнобедренного треугольника АВC, то BD является высотой и медианой треугольника АВC.Теорема о биссектрисе равнобедренного треугольника
Слайд 33 Теорема о средней линии трапеции: средняя линяя трапеции
параллельна основаниям и равна их половине, т.е. если MN-
средняя линия трапеции ABCD,то MN║BC; MN║AD и MN=Теорема о средней линии трапеции
Слайд 34
Теорема о средней линии треугольника:
средняя линия треугольника
параллельна одной из его сторон и равна половине этой
стороны, т.е.если MN-средняя линия ∆АВС, то MN║АС и MN= ACТеорема о средней линии треугольника
Слайд 35
Теорема Пифагора:
квадрат гипотенузы равен сумме квадратов катетов, т.е.
АВ²=АС²+СВ², где АВ - гипотенуза, а АС и СВ
- катеты прямоугольного треугольника АВС.Важными теоремами являются признаки параллелограмма, параллельности двух плоскостей, параллельности прямой и плоскости, перпендикулярности двух плоскостей, подобия треугольников.
Теорема Пифагора
Слайд 37 Теорема Фалеса: если параллельные прямые, пересекающие стороны угла,
отсекают на одной его стороне равные отрезки, то они
отсекают отрезки и на другой его стороне, т.е. если А1А2=А2А3 и А1В1║А2В2║А3В3, то В1В2=В2В3.Теорема Фалеса
Слайд 38 Точка - одно из основных неопределяемых понятий геометрии.
Обозначается: А, В, С,…..Точка вместе с прямой и плоскостью
является отправным понятием при изложении геометрии. Связь между основными понятиями показана в аксиомах. Например, какова бы ни была прямая, существуют точки принадлежащие прямой и точки не принадлежащие этой прямой.Точки А, В, С, принадлежат прямой а
Точки K, N, M, не принадлежат прямой а.
Или такая аксиома: какова бы ни была плоскость, существуют такие точки ей принадлежащие и ей не принадлежащие.
Точки А, В, С принадлежат плоскости α.
В аксиомах также утверждается, что две точки однозначно задают прямую, а три точки однозначно задают плоскость.
Точка
.
К
N
α
А
.
.
В
.
С
М
.
Слайд 39 Торричелли Эванджелиста (1608-1647)- известный итальянский ученный, ученик Галилея.
Сделал род математических открытий.
Внес весомый вклад в создание интегрального
исчисления. Торричелли открыл атмосферное давление и изобрел ртутный термометр.
Торричелли Эванджелиста
Слайд 40 Ат-Туси (1201-1274) - азербайджанский астроном и математик, уроженец
иранского города Тус. Его полное имя в одних переводах
звучит как Насирэддин Туси Ад-Дин Ат-Туси, а в других Насир Ад-Дин Ат-Туси . Этот ученный был выдающимся государственным деятелем. Он организовал обсерваторию, в которую приглашались известные ученые из разных стран.В этом научном центре было создано много замечательных научных трудов.
Ат-Туси написал много трудов по математике, астрономии, минералогии, медицине и логике, которые оказали влияние на европейских ученых.
Ат-Туси
Слайд 41 Угол - гомерическая фигура, состоящая из двух лучей
с общим началом. Общее начало называется вершиной угла, а
сами лучи или полупрямые называются сторонами угла.Точка А – вершина угла, лучи АВ и АС- стороны угла.
Обозначается А или ВАС.
Если стороны угла лежат на одной прямой или являются дополнительными лучами, то такой угол называется развернутым.
Угол
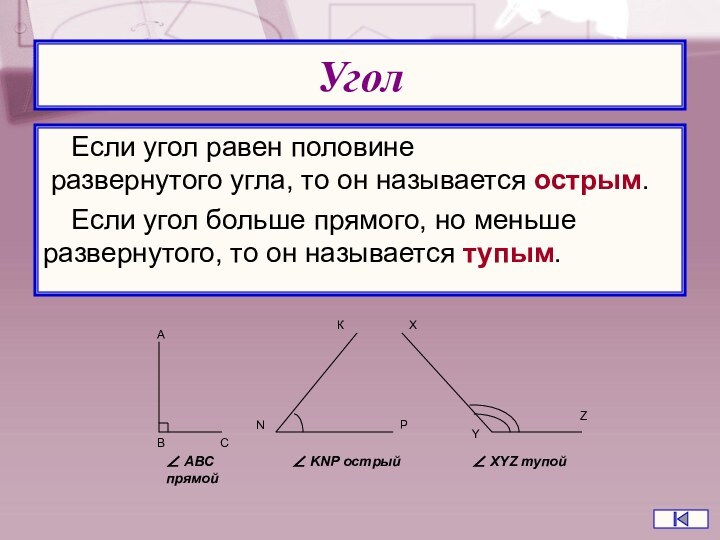
Слайд 42 Если угол равен половине развернутого угла, то он
называется острым.
Если угол больше прямого, но меньше развернутого,
то он называется тупым.Угол
Слайд 43
Текстовые задачи на составление уравнений.
Большая часть текстовых задач
в школьном курсе математики решается путем составления уравнений или
систем уравнений. Поэтому этот метод должен освоить каждый учащийся. Рассмотрим алгоритм решения задач с помощью уравнений:Обозначить неизвестную величину переменной (при решении задач с помощью системы уравнений вводят несколько переменных);
Выразить через нее другие величины;
Составить уравнение (или систему уравнений), показывающее зависимость неизвестной величины от других величин;
Решить уравнение (или систему уравнений);
Сделать проверку при необходимости;
Выбрать из решений уравнения (или системы уравнений)те, которые подходят по смыслу задачи;
Оформить ответ.
Текстовые задачи на составление уравнений можно условно разбить на следующие типы:
Задачи на движение;
Задачи на совместную работу;
Задачи на смеси и сплавы;
Задачи с геометрическим содержанием;
Другие задачи.
Рассмотрим решения задач перечисленных типов.
Текстовые задачи на составление уравнений.
Слайд 44 Задача1. Катер прошел расстояние между пристанями по течению
за 2 ч, а обратно против течения за 3
ч. Найдите собственную скорость катера, если скорость катера реки 2 км/ч.Решение.
Пусть х км/ч – собственная скорость катера, тогда (х+2) км/ч – скорость катера по течению; (х-2) км/ч – скорость катера против течения.
Так как по течению реки катер прошел расстояние между пристанями за 2 часа, а против течения – за 3 часа, то расстояние между пристанями можно выразить двумя выражениями 2(х+2) и 3(х-2). Приравняв эти выражения, получим уравнение:
2(х+2) = 3(х-2);
2х++4=3х-6;
х=10.
Следовательно, собственная скорость катера равна 10 км/ч.
Ответ: 10 км/ч.
Задачи на движение
Слайд 45
Задачи на движение
Задача2. Из пункта А в пункт
В вышел товарный поезд. Спустя 3 ч вслед за
ним вышел пассажирский поезд, скорость которого на 30 км/ч больше скорости товарного поезда. Через 15 ч после своего выхода пассажирский поезд оказался впереди товарного на 300 км. Определите скорость товарного поезда.Решение.
Пусть х км/ч – скорость товарного поезда.
Составим таблицу:
Так как пассажирский поезд прошел на 300 км больше, получаем уравнение:
15(х+30)-18х=300
Решив уравнение, получаем х=50.
Следовательно, скорость товарного поезда 50 км/ч.
Ответ: 50 км/ч.
Слайд 46
Задача1. Имеется руда из двух пластов с содержанием
меди 6% и 11%. Сколько «бедной» руды надо взять,
чтобы получить при смешивании с «богатой» 20 т руды с содержанием меди 8%?Решение.
Переведем проценты в дроби:
6%=0,06; 11%= 0,11;8%=0,08
Пусть необходимость взять х т «бедной» руды, которая будет содержать 0,06х т меди. Тогда «богатой» руды необходимо взять (20-х) т, которая будет содержать 0,11∙ (20-х) т меди.
Так как получившиеся 20 т руды будут содержать 20∙0,08 т меди, то имеет уравнение:
0,06х+0,11∙ (20-х) = 20 ∙ 0,08.
х=12.
Ответ: х=12.
Задачи на смеси и сплавы
Слайд 47
Задача1. Найти площадь прямоугольника, длина которого в 4
раза больше, чем ширина, а площадь численно равна периметру.
Решение.
Пусть
х см – ширина прямоугольника, тогда 4х см – длина прямоугольника, 2(4х+х) см – периметр прямоугольника. Так как площадь равна периметру, получаем следующее уравнение:2(4х+х)= 4х ∙ х или 10х= 4х².
Х1=0
Х2= 2,5.
Условию задачи удовлетворяет только корень = 2,5
Получаем, что ширина прямоугольника равна 2,5 см. Длина = 2,5 ∙ 4=10 см², площадь прямоугольника = 2,5 ∙ 10=25 см².
Ответ: 25 см²
Задачи с геометрическим содержанием





























