- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Метод наименьших квадратов
Содержание
- 2. Количественный анализПроведение количественного анализа, как правило, включает
- 3. Количественный анализТеоретически результаты эксперимента должны укладываться в некоторую зависимость, которую можно выразить формулой.
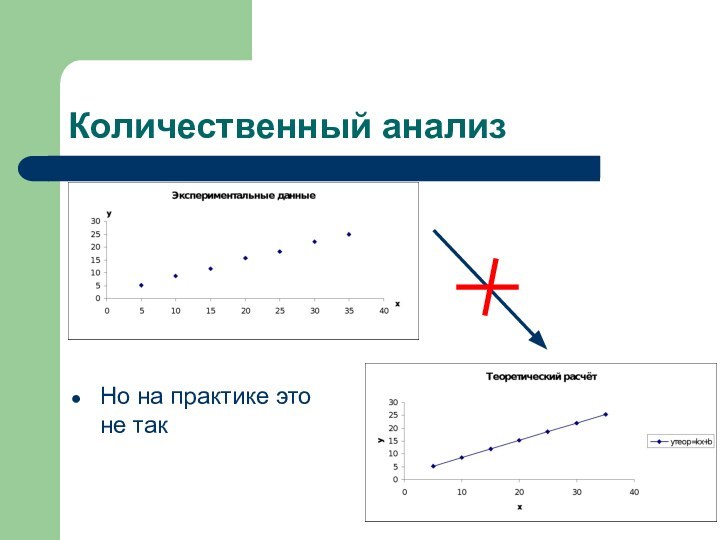
- 4. Количественный анализНо на практике это не так
- 5. Ошибка!Причины:Погрешность измеренийНедостигаемость условий (идеальный газ, стандартное давление и т.д.)Ошибка в расчете
- 6. Метод наименьших квадратовЭто один из методов регрессионного
- 7. Основной принцип метода наименьших квадратовПри замене точного
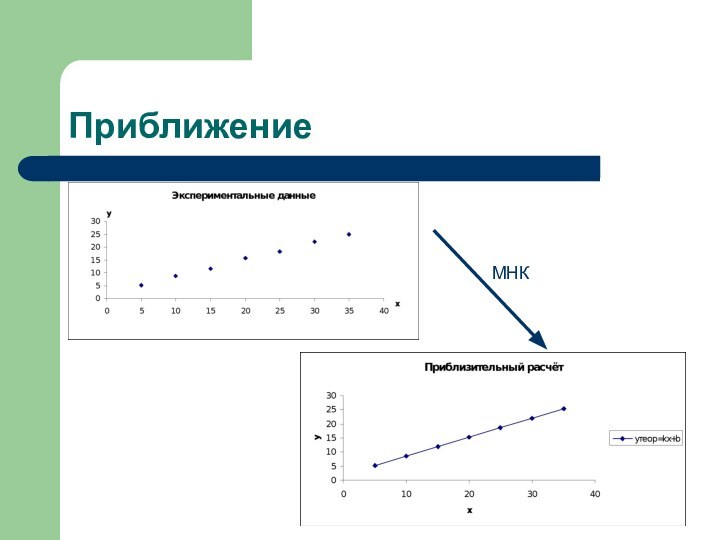
- 8. ПриближениеМНК
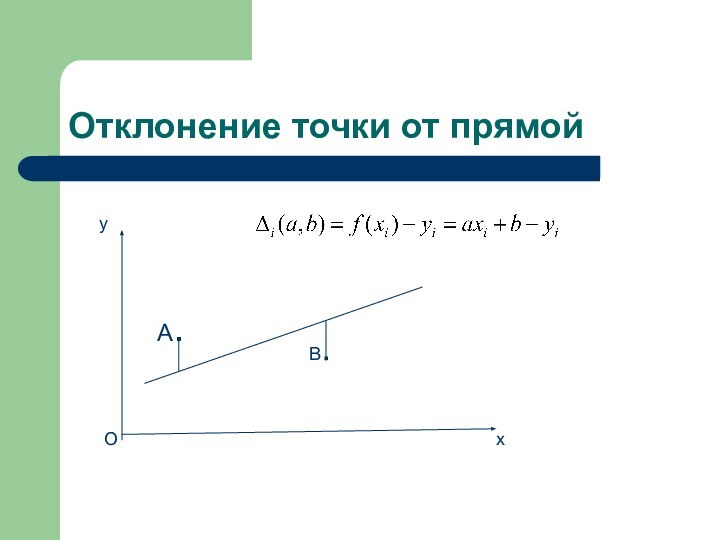
- 9. Отклонение точки от прямойA.xyOB.
- 10. Как учесть отклонение всех точек?В рамках метода наименьших квадратов минимизируется величина: Суммарное отклонение всех точек
- 11. Метод наименьших квадратовПусть нам известно оптимальное значение
- 12. ИтогиВычисление коэффициентов прямой по формулам:
- 13. Метод наименьших квадратов в Microsoft Excel 2003По формулам.Функция ЛИНЕЙНЛИНЕЙНCtrl+Shift+Entera = 0,664357+b = 1,878571
- 14. ОпределенияАналитический сигнал – физическая величина или комбинация
- 15. Градуировочная функцияГрадуировочная функция y = f(x) определяется
- 16. Необходимодоопределить функцию (между точками)минимизировать погрешностьвыбрать вид зависимости. .....xy0
- 17. АппроксимацияАппроксимация – замена одних математических объектов другими,
- 18. Пример: Колориметрический анализДано n стандартных растворов и
- 19. Решение:Закон Бугера-Ламберта-Бера: A= ε·C·lI и
- 20. Решение:Проводят реакцию с реагентом, дающим с заданным
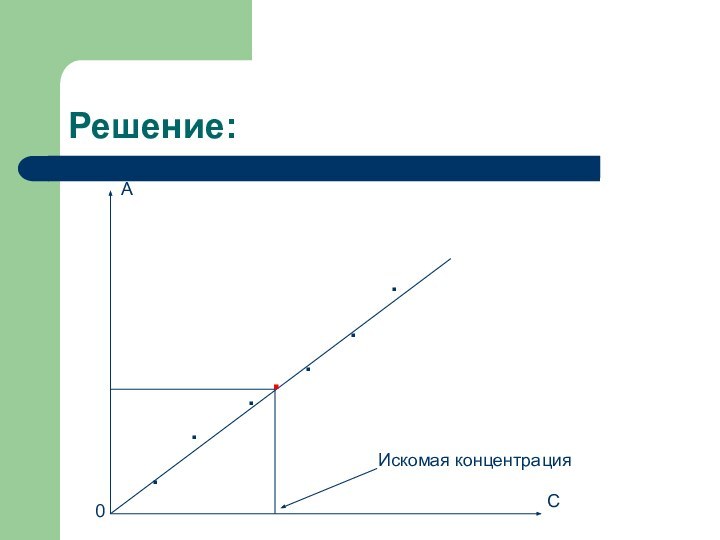
- 21. ......CA0.Искомая концентрацияРешение:
- 22. Выводы:Метод наименьших квадратов, а также его различные
- 23. Скачать презентацию
- 24. Похожие презентации
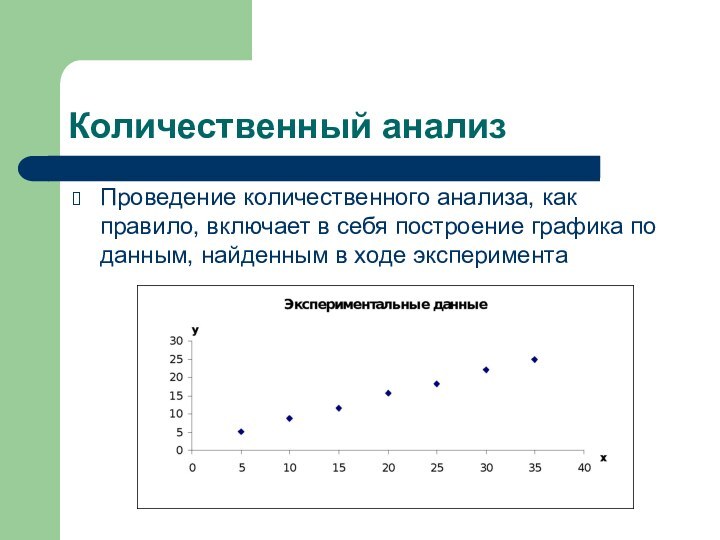
Количественный анализПроведение количественного анализа, как правило, включает в себя построение графика по данным, найденным в ходе эксперимента
















Слайд 2
Количественный анализ
Проведение количественного анализа, как правило, включает в
себя построение графика по данным, найденным в ходе эксперимента
Слайд 3
Количественный анализ
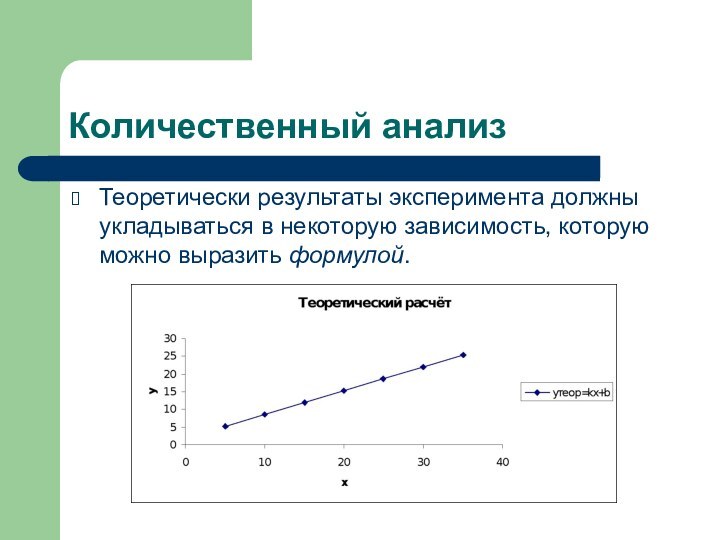
Теоретически результаты эксперимента должны укладываться в некоторую
зависимость, которую можно выразить формулой.
Слайд 5
Ошибка!
Причины:
Погрешность измерений
Недостигаемость условий (идеальный газ, стандартное давление и
т.д.)
Ошибка в расчете
Слайд 6
Метод наименьших квадратов
Это один из методов регрессионного анализа
для оценки неизвестных величин по результатам измерений, содержащих случайные
ошибки.Метод наименьших квадратов применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Слайд 7
Основной принцип метода наименьших квадратов
При замене точного (неизвестного)
параметра модели приблизительным значением необходимо минимизировать разницу между экспериментальными
данными и теоретическими (вычисленными при помощи предложенной модели).
Слайд 10
Как учесть отклонение всех точек?
В рамках метода наименьших
квадратов минимизируется величина:
Суммарное отклонение всех точек
Слайд 11
Метод наименьших квадратов
Пусть нам известно оптимальное значение a.
Тогда S зависит только от b. Для того, чтобы
найти минимум, надо приравнять производную к нулю.
Слайд 13
Метод наименьших квадратов в Microsoft Excel 2003
По формулам.
Функция
ЛИНЕЙН
ЛИНЕЙН
Ctrl+Shift+Enter
a = 0,664357
+
b = 1,878571
Слайд 14
Определения
Аналитический сигнал – физическая величина или комбинация физических
величин, функционально связанная с содержанием компонента в пробе.
Градировочная функция
– функция f связывающая содержание компонента в пробе и аналитический сигнал. Градуировка – экспериментальное или расчетное установление градуировочной характеристики, построение графика градуировочной функции.
Слайд 15
Градуировочная функция
Градуировочная функция y = f(x) определяется методами
регрессионного анализа.
Прямо через точки проводить ломаную и считать
ее градуировочной функцией нельзя, т.к. измеряемый сигнал содержит погрешность.
Слайд 16
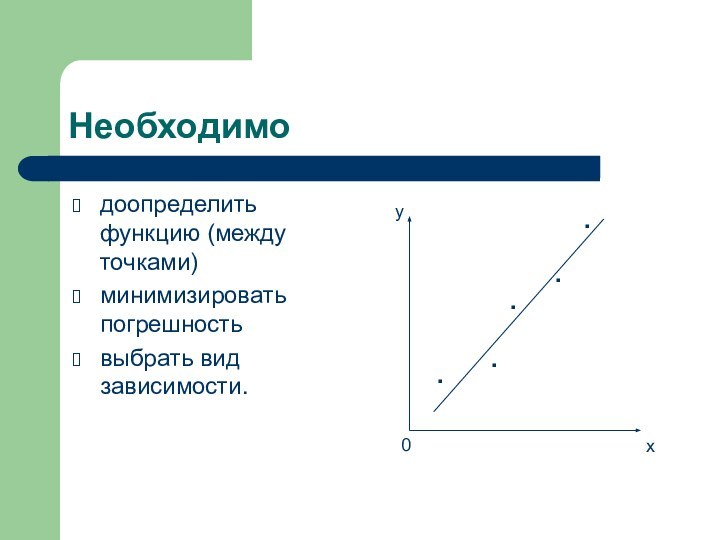
Необходимо
доопределить функцию (между точками)
минимизировать погрешность
выбрать вид зависимости.
.
.
.
.
.
x
y
0
Слайд 17
Аппроксимация
Аппроксимация – замена одних математических объектов другими, в
том или ином смысле близкими к исходным.
Вид функции
зависимости выбирается исходя из внешней информации (расположения точек на плоскости) и из общих соображений относительно физических и химических законов, связывающих аналитический сигнал с содержанием определяемого компонента (например, построение градуировки в спектрофотометрии опирается на закон Бугера-Ламберта-Бера).
Слайд 18
Пример:
Колориметрический анализ
Дано n стандартных растворов и раствор неизвестной
концентрации. При помощи фотоколориметра определить содержание вещества в растворе
с неизвестной концентрацией.КОЛОРИМЕТРИЯ (от лат. color — цвет и ...метрия), оптический метод анализа, в котором концентрация вещества определяется по интенсивности окраски раствора или светопоглощения.
Слайд 19
Решение:
Закон Бугера-Ламберта-Бера:
A= ε·C·l
I и I0 – конечная или
исходная интенсивность света. A – оптическая плотность раствора ε – коэффициент
светопоглощения (величина, постоянная для данного окрашенного вещества) С – концентрация раствора l – толщина светопоглощающего раствораI = I0-ε·C·l
ИЛИ
Слайд 20
Решение:
Проводят реакцию с реагентом, дающим с заданным веществом
окрашенные растворы.
При помощи фотоколориметра определяют оптическую плотность полученных растворов
известной концентрации. Строят градуировочную прямую концентрации от оптической плотности. (Именно на этом этапе используется метод наименьших квадратов)Определяют оптическую плотность раствора неизвестной концентрации.
По графику находим искомое содержание.
Слайд 22
Выводы:
Метод наименьших квадратов, а также его различные модификации
широко используется в аналитической химии, в частности, при построении
градуировочной модели.В рамках метода наименьших квадратов минимизируется величина сумма квадратов отклонений действительных (экспериментальных) значений от теоретических.





























