- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок-соревнование
Содержание
- 2. 12345678
- 4. Теорема: Площадь параллелограмма равна произведению его основания на высоту
- 5. Теорема: Площадь параллелограмма равна произведению его основания
- 6. Теорема: Площадь параллелограмма равна произведению его основания на высотуДоказательство:ABCK-трапецияABCK=ABCD+CDKABCK=BHKС+ABH
- 7. Теорема: Площадь параллелограмма равна произведению его основания
- 8. Теорема: Площадь параллелограмма равна произведению его основания на высотуSABCK=SABCD+SCDKSABCK=SBHKC+SABH
- 9. Теорема: Площадь параллелограмма равна произведению его основания на высотуSABCD= SBHKC=S
- 10. !Теорема: Площадь параллелограмма равна произведению его основания
- 11. Теорема: площадь треугольника равна половине произведения его основания на высотуCABH
- 12. Теорема: площадь треугольника равна половине произведения его
- 13. Теорема: площадь треугольника равна половине произведения его основания на высотуДоказательство: CABHD
- 14. Теорема: площадь треугольника равна половине произведения его основания на высотуCABDДоказательство:ABC = DCB т.к.1.CB-общая2.AB=DC3.AC=DB
- 15. Теорема: площадь треугольника равна половине произведения его основания на высотуCABDДоказательство:S ABDC=2 SABC
- 16. Теорема: площадь треугольника равна половине произведения его основания на высотуДоказательство:S ABDC=CH AB
- 17. ! Теорема: площадь треугольника равна половине произведения его основания на высотуДоказательство:SABC=1/2 CH ABЧто и требовалось доказать.
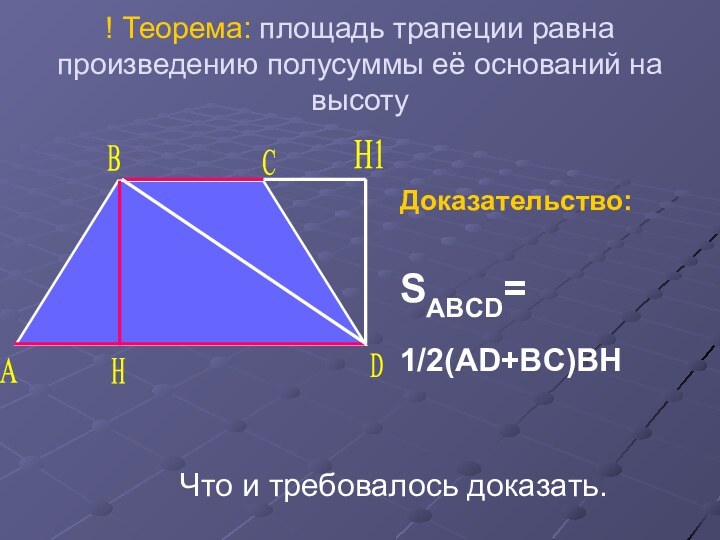
- 18. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуCABHD
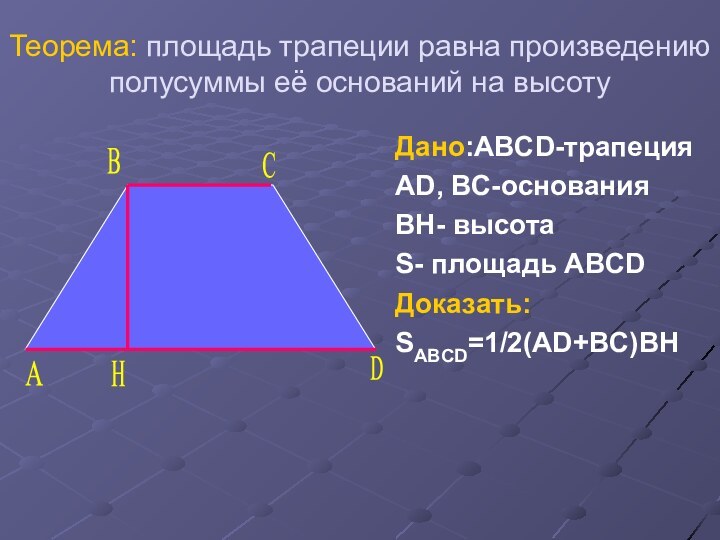
- 19. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуCABHDДано:ABCD-трапецияAD, BC-основанияBH- высотаS- площадь ABCDДоказать:SABCD=1/2(AD+BC)BH
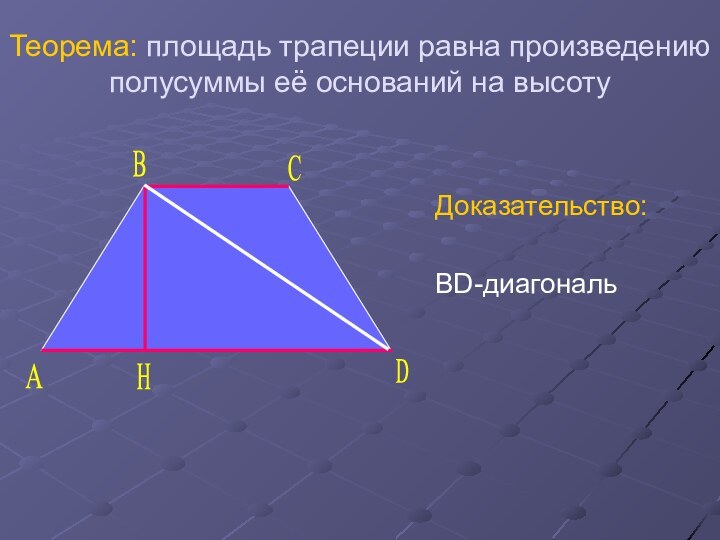
- 20. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуДоказательство:BD-диагональ
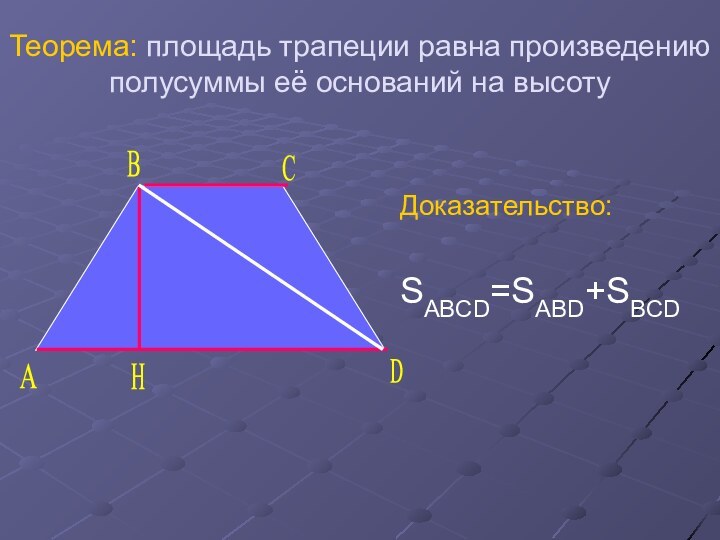
- 21. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуДоказательство:SABCD=SABD+SBCD
- 22. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуДоказательство:Дополнительное построение.H1
- 23. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуCABHDДоказательство:SABD=1/2 BH ADH1
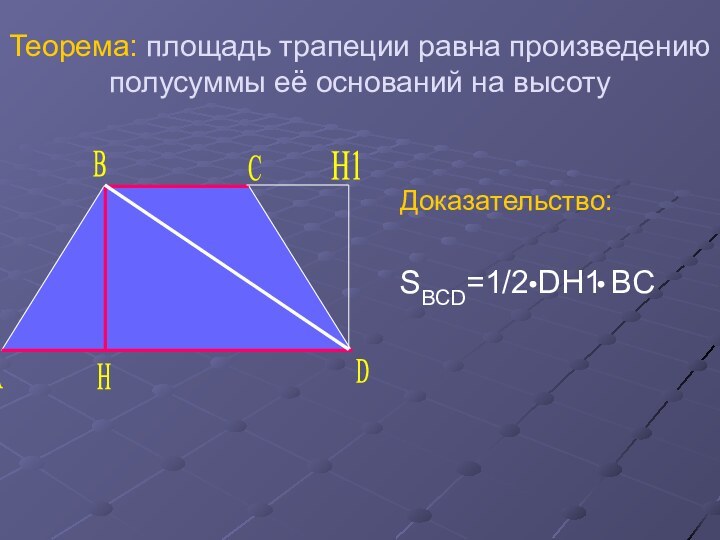
- 24. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуДоказательство:SBCD=1/2 DH1 BCH1
- 25. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуCABHDДоказательство:DH1=BH SBCD=1/2 BH BCH1
- 26. Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуДоказательство:SABCD=1/2 BH AD+1/2 BH BCH1
- 27. ! Теорема: площадь трапеции равна произведению полусуммы её оснований на высотуCABHDДоказательство:SABCD=1/2(AD+BC)BHH1Что и требовалось доказать.
- 28. Решение задач
- 29. Задача №1Дано:ABCD-параллелограммAB = 6 смAD= 10 смA=300Найти: S ABCD -?CABD30010 см6 см
- 30. Задача №1Ответ: S ABCD =30см2CABD30010 см6 см
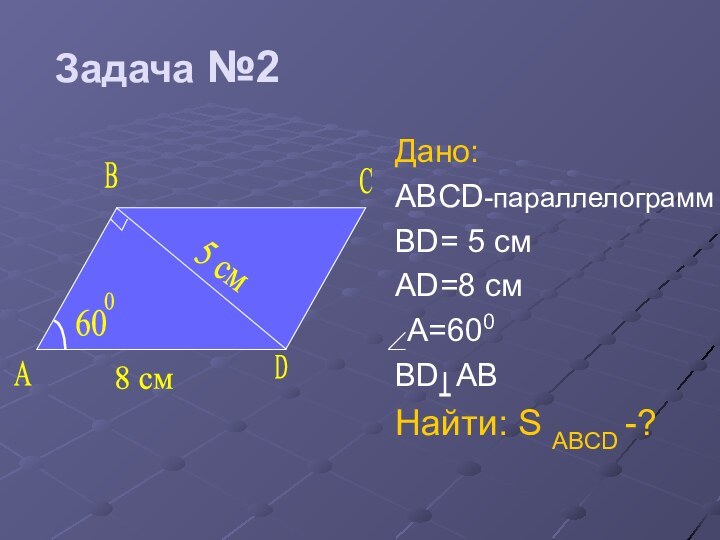
- 31. Задача №2Дано:ABCD-параллелограммBD= 5 смAD=8 cм A=600BD ABНайти: S ABCD -?CABD6005 cм8 см
- 32. Задача №2Ответ: S ABCD =20см2CABD6005 cм8 см
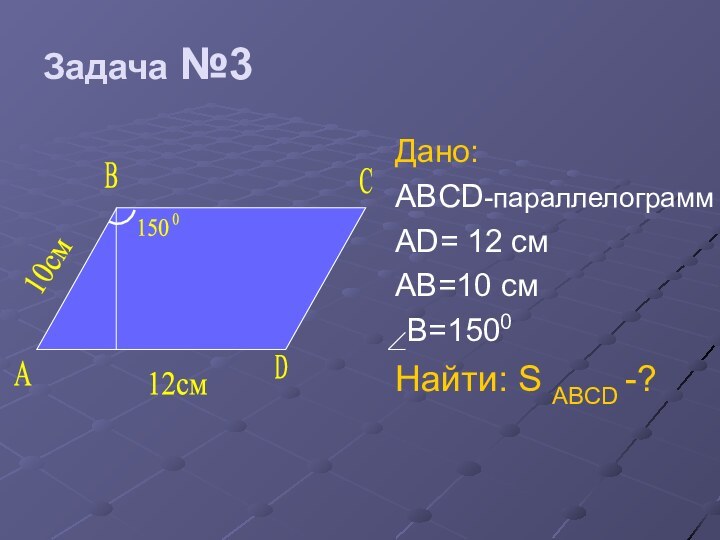
- 33. Дано:ABCD-параллелограммAD= 12 смAB=10 cм B=1500Найти: S ABCD -?CABD150012cм10cм Задача №3
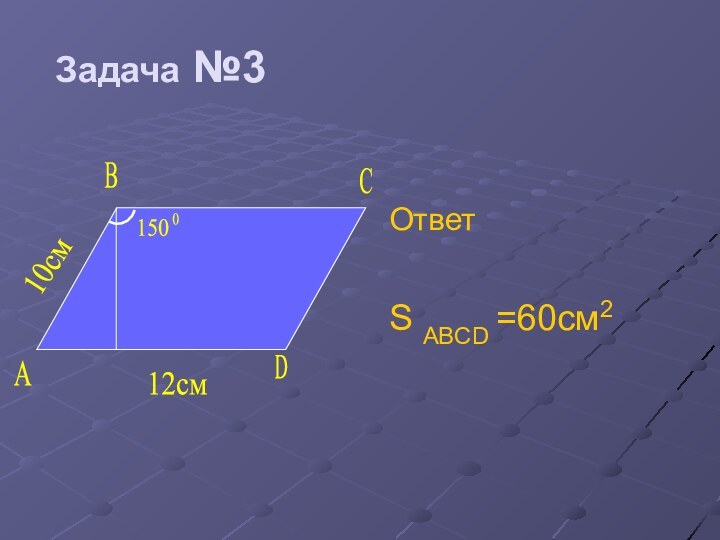
- 34. Задача №3Ответ S ABCD =60см2CABD150012cм10cм
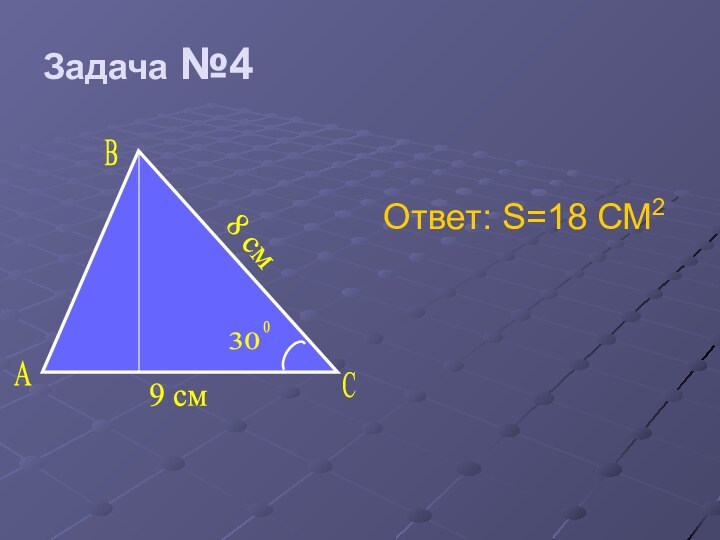
- 35. Дано:ABC-треугольникBC= 8 смAC=9 cм C=300Найти: S ABC-?CAB9 см8 см Задача №4
- 36. Ответ: S=18 СМ2CAB9 см8 см Задача №4
- 37. Дано:ABCD-квадратAB=5 смKD=4 смНайти: S ABC-? Задача №5CABDK4 см5 см
- 38. Ответ:S ABC=15 см2 Задача №5CABDK
- 39. Задача №6CABDДано:ABC-треугольникAD= 7смADB=1350 C=900Найти: S ABC-?8 см7 см
- 40. Задача №6CABDОтвет S ABC=60 см28 см7 см
- 41. Домашняя работаП.51-53 (повторить)В 1-7, №506, №518(а)Дополнительно №518 (б)
- 42. Скачать презентацию
- 43. Похожие презентации
12345678



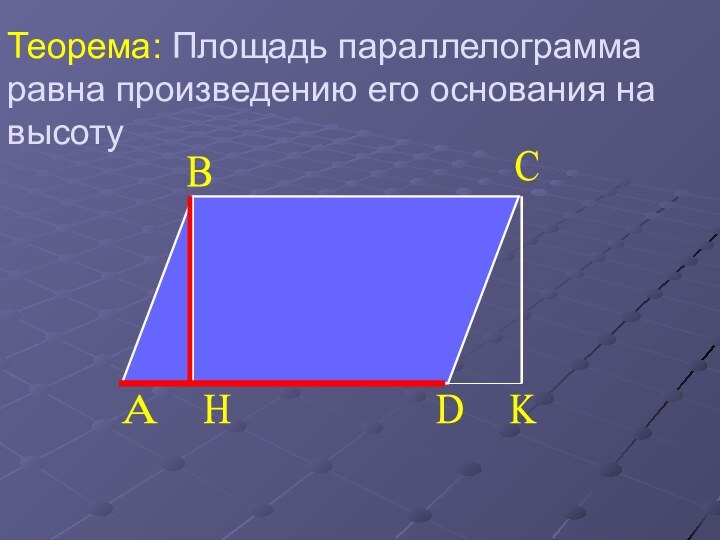


























Слайд 5 Теорема: Площадь параллелограмма равна произведению его основания на
высоту
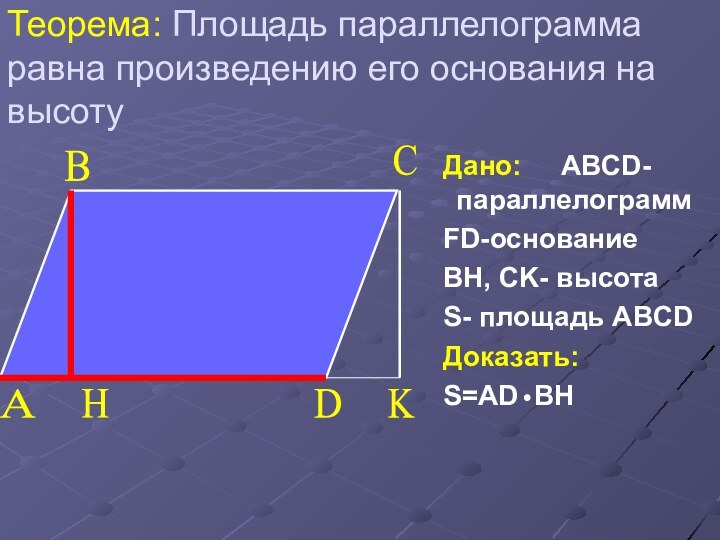
Дано: ABCD-параллелограмм
FD-основание
BH, CK- высота
S- площадь ABCD
Доказать:
S=AD BH
Слайд 6 Теорема: Площадь параллелограмма равна произведению его основания на
высоту
Доказательство:
ABCK-трапеция
ABCK=ABCD+CDK
ABCK=BHKС+ABH
Слайд 7 Теорема: Площадь параллелограмма равна произведению его основания на
высоту
ABH = CDK
AB
= CD1 = 2
Значит, SABH=SCDK
1
2
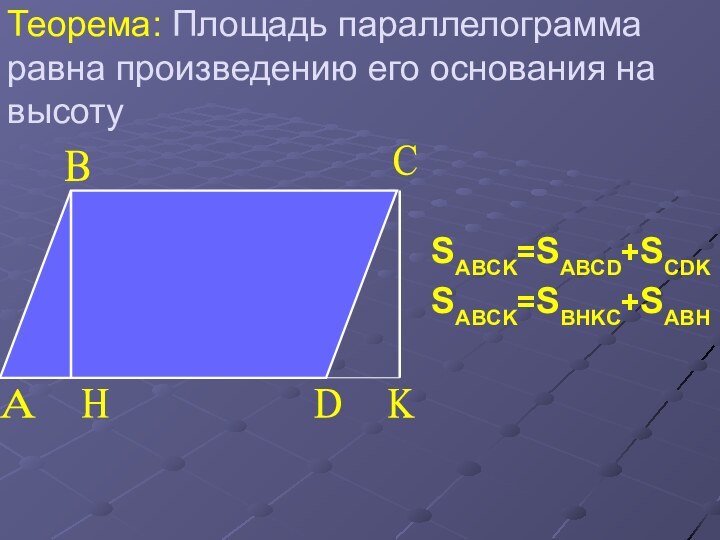
Слайд 8 Теорема: Площадь параллелограмма равна произведению его основания на
высоту
SABCK=SABCD+SCDK
SABCK=SBHKC+SABH
Слайд 10 !Теорема: Площадь параллелограмма равна произведению его основания на
высоту
SBHKC= BC BH
Т.к. BC = AD, то
S = AD BH
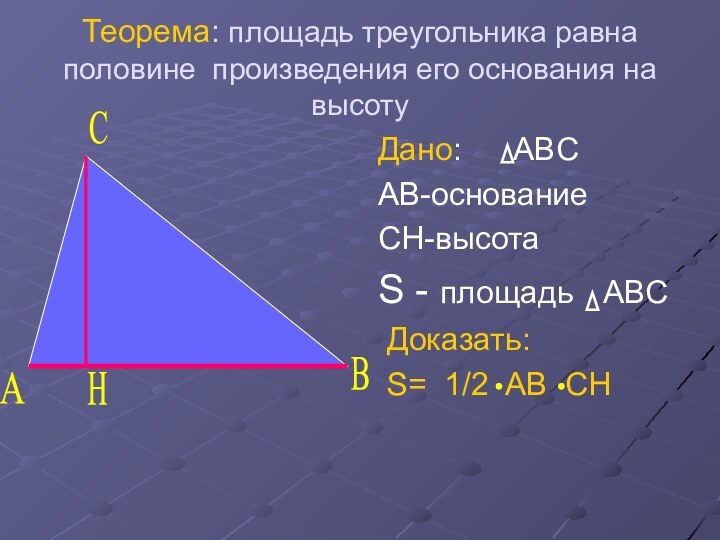
Слайд 12 Теорема: площадь треугольника равна половине произведения его основания
на высоту
Дано: ABC
AB-основание
CH-высота
S - площадь ABC
Доказать:S= 1/2 AB CH
C
A
B
H





























