Презентация на тему Небесная механика

эллипса
x acos
y bsin
Длина эллипса
2

 
x
0

L dl

 y d 4aE(e)
2 2



/2



E(e) d 1e

sin
2


-

полный эллиптический интеграл 2-го рода

2

0

Длина окружности

E(0) / 2

L 2a

частица находится в невесомости.
Теорема Ньютона: обобщение на эллипсоидальный слой

r1
 dS r2
2
2
1
2
2
2
F r

2
dS r
 
1
1 2
2

F dm r



1

1

2

2

1

2

1

2

M S

F  Const

2
r r

2

4Ga, ra
 
внутр











     

внутр
шар

сфера








r

dr
r

r

a

2







 
r dr


внутр
шар

   

4

G










0

r

GM


внутр
шар

 

(3
3
a

a r )

2

2

2

GM
r


внеш
шар




ra

out
c2
r
 0




  
r
2
r r
r,out0,

GM
r

out

2

2













out


G r2

1

2

c
1
r

  

ra 

2

    

r  4 G

inner

c2







  

r

2
r r

3

и силы
ra
out
inner

ra
ra
Потенциал шара


GM
r


, ra


шар





GM
(3
a3
a r ), r





2

2





2

шар….

точку с силами,
одинаково направленными, а по величине пропорциональными их

F M



x

/

/

F M

x

Теорема Ляпунова
Шар обладает минимальной потенциальной энергий

эквивалентен потенциалу
стержня мнимой длины.
Метод эквигравитирующих стержней

R (t )


R R


N
R

i

i



0




(0)



j

i

i

j

3

R R (t )
i

R
ij

j1

i

0

Порядок системы 6(n+1)

Первые интегралы:


















m R  a,


m R  atb

закон движения центра масс

i i

i i

i

i

 


i i

Rm R  I

закон сохранения момента количества движения

i

i

E TU

закон сохранения энергии

tot

В скалярном виде 10 первых интегралов в произвольной инерциальной с.к.

1
3




R  Gm
R
(0)
 R (t

1,2

1,2



0

1

2

R
12







R R
1 2
3


R (t )
1,2 0



R

(0)



1,2

R  Gm

2

1

R

12



m

i i

0

Барицентрическая с.к.

i











m


3
2
m m )

1



G (
G (

 0
 0



1

2

3

1

2

1











m


3
1
m m )

2
3
2





2

2

1

2

r(t )
0




r
 r(t )
0
Первые интегралы:




rr  I
момент

E  TU

tot

Порядок системы =6, но 4 первых (в скалярах) интегралов. Не хватает…..




rI
 0
Интеграл Лапласа






r

вектор Лапласа
rI 
r
Уравнения связи между первыми





I 0

5

независимых первых интегралов =>

Вектор момента и вектор Лапласа перпендикулярны

задача двух тел в относит с.к.
(система 6-го порядка) сводится к одному
уравнению

2

 

E I
tot

2

2

)  r
r
 
I

2

r

p
ecos

r1





p I

2

e 

p
dn
r2
n  I


(1
n
2
0
n 1e E
tg

tg
1e 2

2

Уравнение Кеплера

a3/2

E esinE  n(t )

 
T 2

G(M  m)



u
2




c
2
I
2
I
2
Релятивистская задача
2
rgmc2

du 
d 
n
m c
2 2
(1
E2
)

r u
g
3
u
2

u






I

2

I

2

m c
2 4

Максимальное смещение перигелия наблюдается для Меркурия и составляет
43’’ за 100 лет.

 
y
)

U
2
1
r r
1
2

z

z
2


2
V 2U

J

C - интеграл Якоби (интеграл относительной энергии)
J

C
U(x, y,z) (x
 y
) 
2
2
1
2
2
r

1

2

Поверхности нулевой скорости

2

 2



  

CJ

2

2

2

n (x y )

1

2

r r

1

2

CJ - интеграл Якоби

r 1
1
2
2
1
L1,L2
1/3






2
31
r
2

L3
2
7
12 1
  
r 1
1

 F
возм


F  F
возм
0
На малом интервале – невозмущенное

Планетные уравнения Лагранжа

Uвозм - возмущающий потенциал

dE




(E ,U )
i

i



 
E (i, , ,e, p, )

j

возм

dt

i

возмущенный Юпитером
a a
0
e e  A(cos cos)
0
0


 Bt
0
 Ct
0

  
 
sin(k M


cos(k M k M )
1 1 2 2

k ,k

k ,k

E E A (t t )




1

2

1

2



k n k n



0

0

0

1

1

2

2

k n k n

k1,k2

1 1

2 2

1 1

2 2

k1,2 – собственная частота движения
планеты и частота возмущающей силы (m2)

A(k ,k )

Периодические возмущения :

Amlp
T

1

2

k n k n

1

1

2 2

2



k n k n

1

1

2 2

на резонансной орбите с Юпитером
a 5.20
TA
TJ
2n n

J

 0.5

J

a 3.27

A

Юпитер-Сатурн
TJ
TS
2

5
Эксцентриситет орбиты каждой из планет периодически изменяется
с периодом

возмущения
k n k n
1
1
2 2
2
k1n1
k n k




1 1

T

1

1

2 2

Периоды возмущений порядка орбитального периода, амплитуда мала.

•

Долгопериодические возмущения (при малых k1,k2)

k n k n 0

Отношение средних движений =простой дроби

1

1

2 2

n k



1

2
1

- резонансное состояние

n k
2

(1981г.)
1991г.
– официально назван
в честь бога пастухов
Расположен внутри люка Энке
и

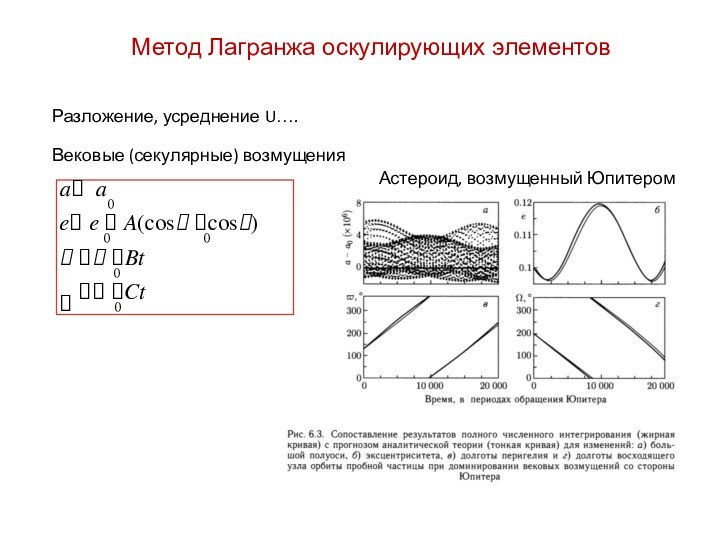
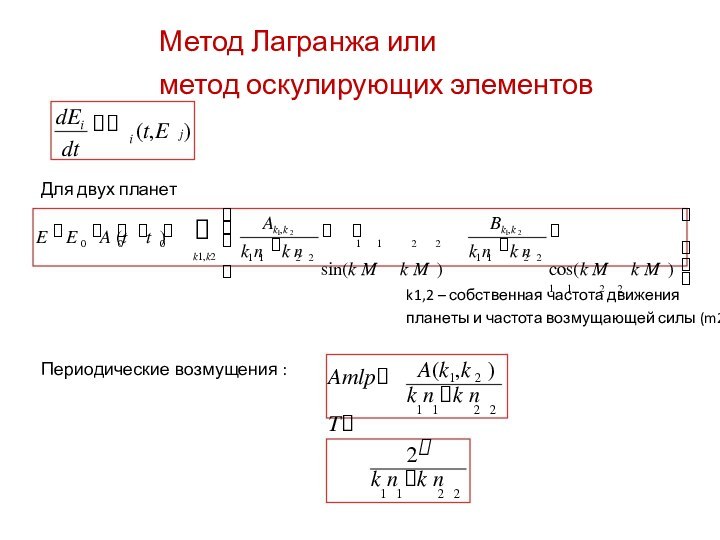
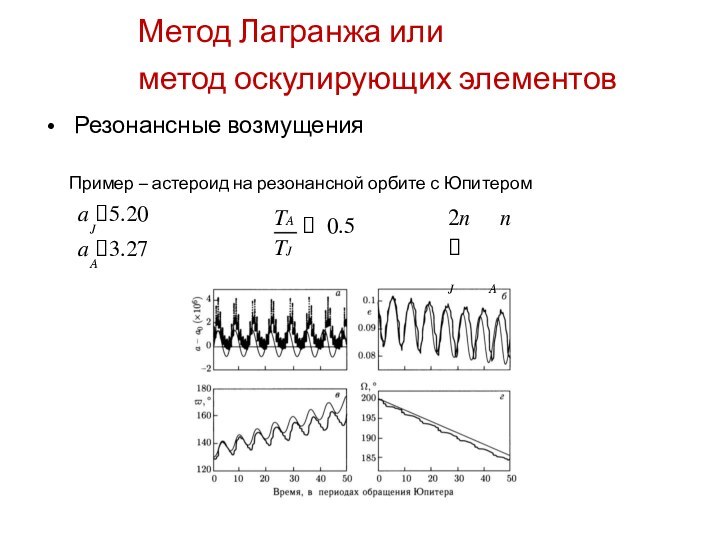
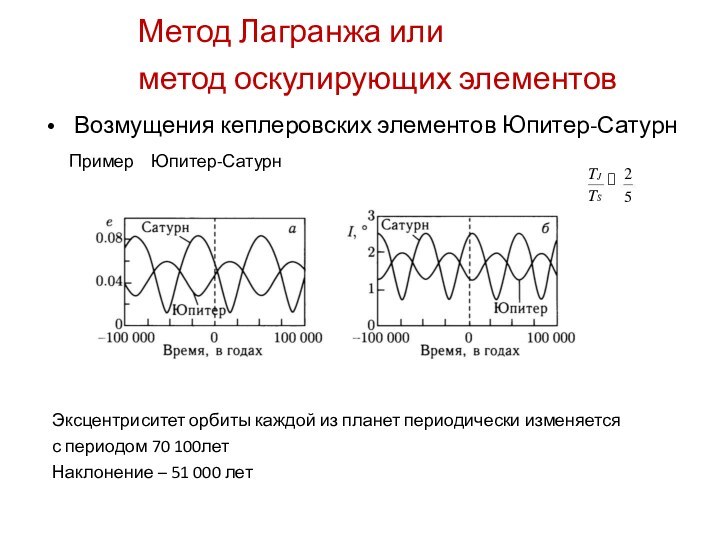
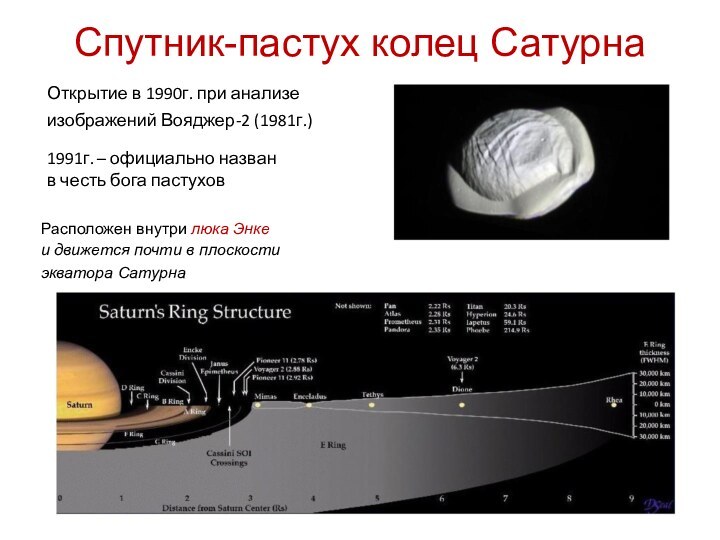
the Keeler gap in Saturn's rings is made all

From the size of the waves seen in the scalloped edges of the Encke gap, imaging scientists were
able to estimate the mass of Pan. They expect to do the same eventually with S/2005 S1.
This image was obtained with the Cassini spacecraft narrow-angle camera on May 2, 2005, at a
distance of about 594,000 kilometers from Saturn.

https://www.nasa.gov/mission_pages/cassini/multimedia/pia06237.html

на эклиптику

выделенную плоскость фазового пространства.
Для траектории на плоскости:
4-
х мерное фазовое

 
x, y,x, y)

(

Одну из переменных можно исключить,
воспользовавшись интегралом Якоби
или полной энергией => 3D фазовое пр-во

(

x, y,x)

Выделяем одну из плоскостей, например, y=0 .

(

x,x)

Т.о. получаем проекцию на фазовую плоскость


Потенциал Хенона-Хейлиса
U(x, y)  x
2
 y
2
 2x
2
3


2
E

N=50 – число частиц

150

периодов

Траектория одной из частиц

150

периодов

x
2 
y  y
3 
2
 y
2


2

3




2



N=50 – число частиц

a few 100 periods

E =1/40
tot


Потенциал Хенона-Хейлиса
U(x, y)  x
2
 y
2
2x
2
3


2
E


Потенциал Хенона-Хейлиса
U(x, y)  x
2
 y
2
2x
2
3


2
E


Потенциал Хенона-Хейлиса
U(x, y)  x
2
 y
2
2x
2
3


2
E