- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Некоторые доказательства теоремы Пифагора
Содержание
- 2. Краткая биографическая справкаФормулировка теоремыПростой способДоказательство ЭпштейнаДоказательство БхаскариДоказательство
- 3. Родился около 570, умер около 500 до
- 4. Отцом Пифагора был Мнесарх, резчик по драгоценным
- 5. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.Формулировка Пифагора
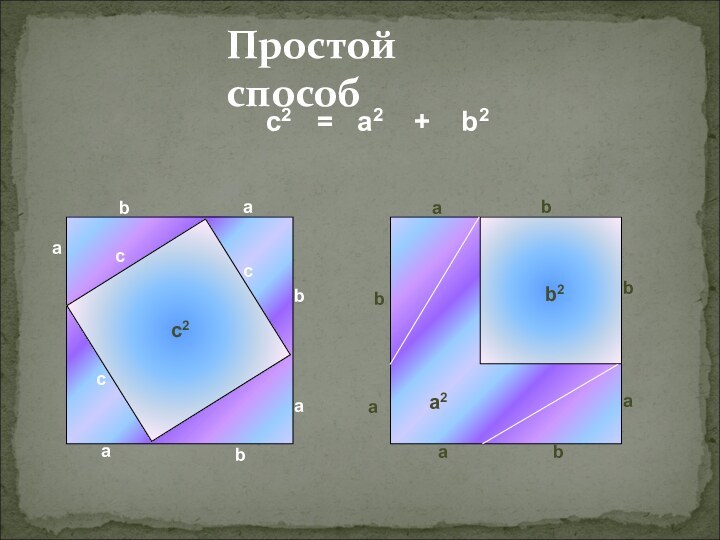
- 6. Простой способc2 = a2 + b2
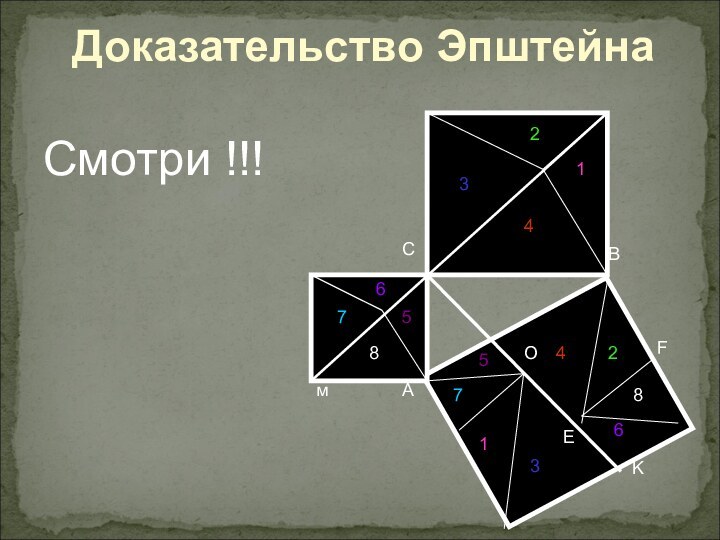
- 7. Доказательство ЭпштейнаСмотри !!!
- 8. Доказательство Бхаскариc2 - 4 (1/2 a b)=(b
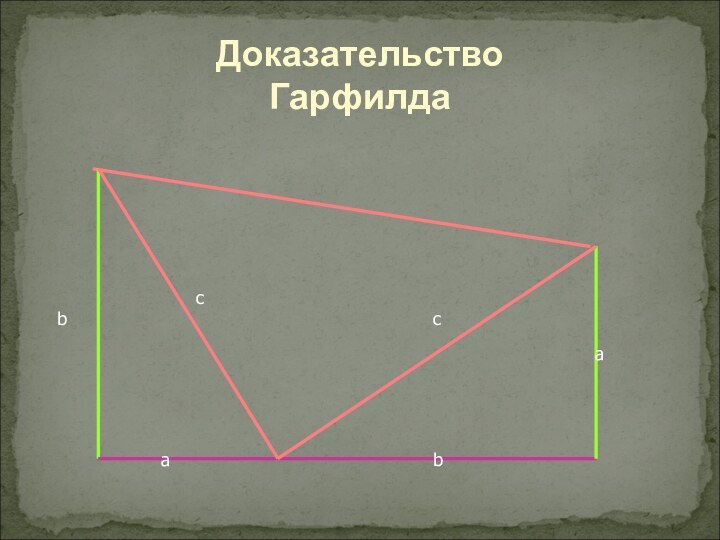
- 9. Доказательство Гарфилда
- 10. Доказательство:S трапеции = ½ (a + b)
- 11. Решение:1). ½ ( a2 + a b
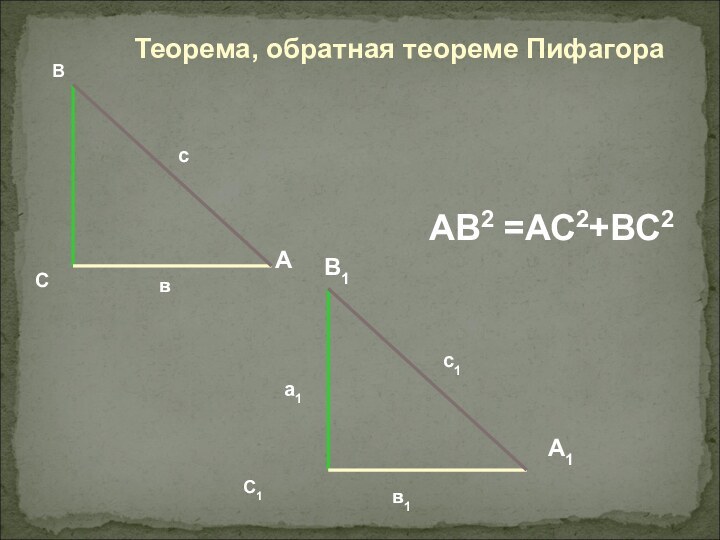
- 12. Теорема, обратная теореме ПифагораС1СВАВ2 =АС2+ВС2
- 13. Пифагоровы треугольникиПо теореме, обратной теореме ПИФАГОРА, треугольник
- 14. Египетский треугольникЭтим свойством пользовались еще древние египтяне
- 15. Египетский треугольникТреугольник со сторонами 3, 4 и
- 16. Египетский треугольниксвязывали ее концы и растягивали на
- 17. Скачать презентацию
- 18. Похожие презентации
Краткая биографическая справкаФормулировка теоремыПростой способДоказательство ЭпштейнаДоказательство БхаскариДоказательство ГорфилдаТеорема, обратная теореме ПифагораПифагоровы треугольникиЕгипетский треугольник Содержание :









Слайд 2
Краткая биографическая справка
Формулировка теоремы
Простой способ
Доказательство Эпштейна
Доказательство Бхаскари
Доказательство Горфилда
Теорема,
обратная теореме Пифагора
Слайд 3 Родился около 570, умер около 500 до н.э.
Древнегреческий философ и математик, основатель пифагорейской школы;
Известно, что Пифагор
покинул свой родной остров Самос в Эгейском море у берегов Малой Азии в знак протеста против тирании правителя.Он много путешествовал по странам Востока : был в Египте, в Вавилоне, где познакомился с восточной математикой.
Пифагор впервые разделил числа на четные и нечетные, простые и составные…
Пифагор
Слайд 4 Отцом Пифагора был Мнесарх, резчик по драгоценным камням.
Имя же матери Пифагора неизвестно. По многим античным свидетельствам,
родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.
Слайд 5 Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна
сумме площадей квадратов, построенных на его катетах.
Формулировка Пифагора
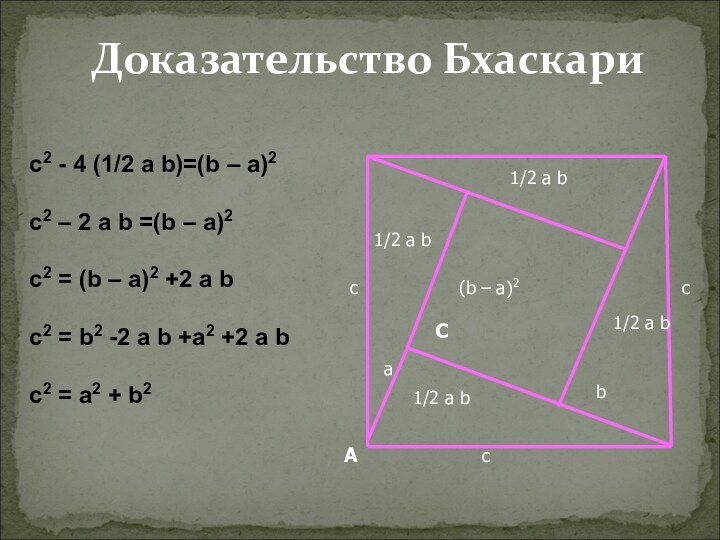
Слайд 8
Доказательство Бхаскари
c2 - 4 (1/2 a b)=(b –
a)2
c2 – 2 a b =(b – a)2
c2 =
(b – a)2 +2 a bc2 = b2 -2 a b +a2 +2 a b
c2 = a2 + b2
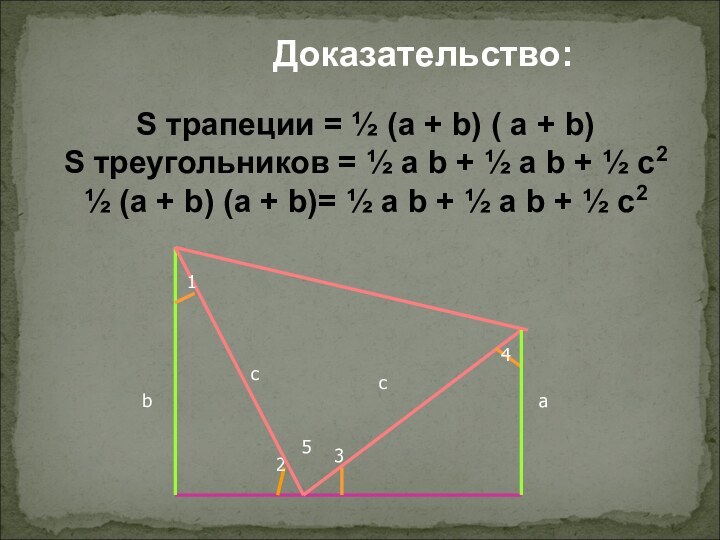
Слайд 10
Доказательство:
S трапеции = ½ (a + b) (
a + b)
S треугольников = ½ a b
+ ½ a b + ½ с2½ (a + b) (a + b)= ½ a b + ½ a b + ½ c2
Слайд 11
Решение:
1). ½ ( a2 + a b +
a b + b 2) = ½ a2 +
½ a b + ½ a b + +½ b2= ½ a2 + a b + ½ b22). ½ a b + ½ a b + ½ c2 = a b + ½ c2
Приравниваем 1). и 2).
½ a2 + a b + ½ b2= a b + ½ c2
½ a2 + ½ b2 = ½ c2
c2=a2 + b2
Слайд 13
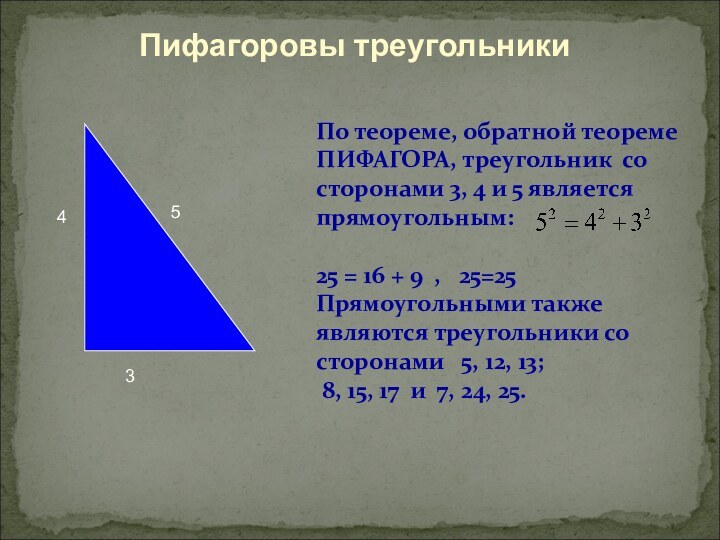
Пифагоровы треугольники
По теореме, обратной теореме ПИФАГОРА, треугольник со
сторонами 3, 4 и 5 является прямоугольным:
25 =
16 + 9 , 25=25Прямоугольными также являются треугольники со сторонами 5, 12, 13;
8, 15, 17 и 7, 24, 25.
Слайд 14
Египетский треугольник
Этим свойством пользовались еще древние египтяне для
построения прямых углов при планировке земельных участков и сооружений
зданий.
Слайд 15
Египетский треугольник
Треугольник со сторонами 3, 4 и 5
часто называют ЕГИПЕТСКИМ ТРЕУГОЛЬНИКОМ, так как он был известен
еще древним египтянам.Для построения прямых углов египтяне поступали так:
на веревке делали метки, делящие ее на 12 равных частей,
Слайд 16
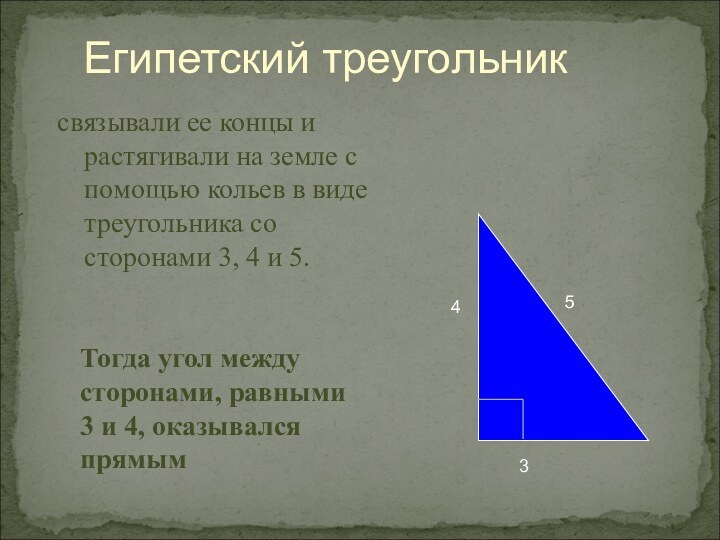
Египетский треугольник
связывали ее концы и растягивали на земле
с помощью кольев в виде треугольника со сторонами 3,
4 и 5.Тогда угол между
сторонами, равными 3 и 4, оказывался прямым