найти маршрут, который содержит все вершины или ребра графа
– обход.Часто требуется, чтобы длина этого маршрута была минимальной (для взвешенных графов), или ограничивается число проходов по одному и тому же элементу графа.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















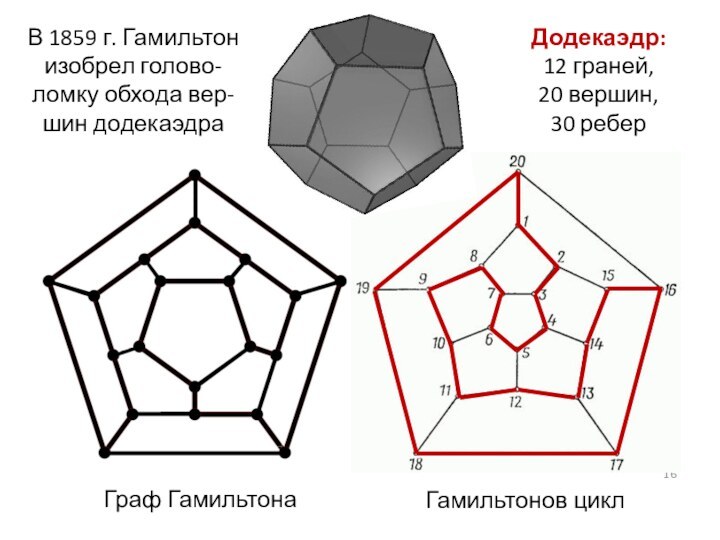





Эйлеров граф можно нарисовать одним росчерком пера.
5
3
3
3
3
3
4
2
Постановка задачи
Кенигсбергские мосты
Теорема Эйлера (1736 г.)