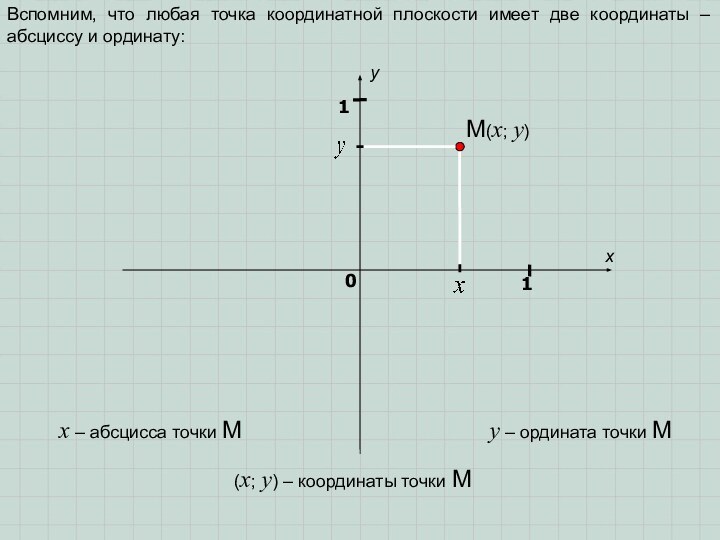
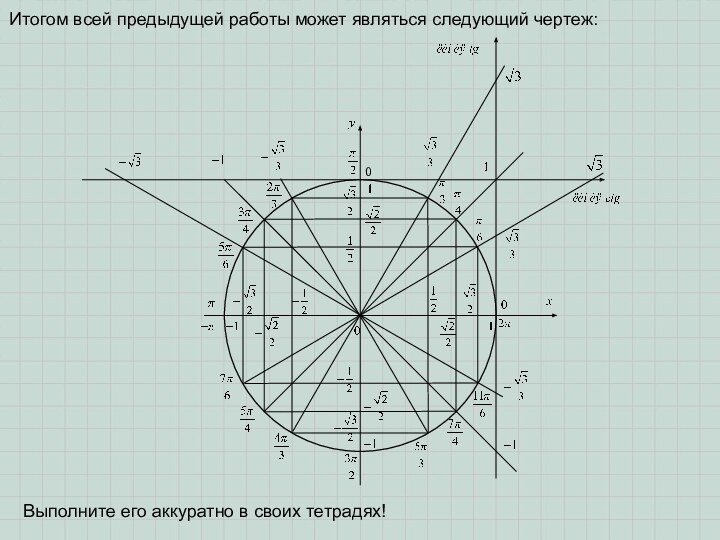
координаты – абсциссу и ординату:
y – ордината точки M
x
– абсцисса точки MM(x; y)
(x; y) – координаты точки M
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
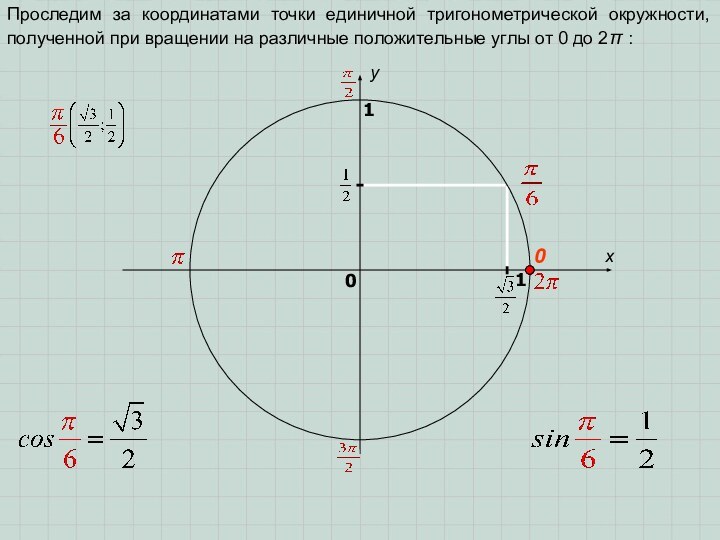
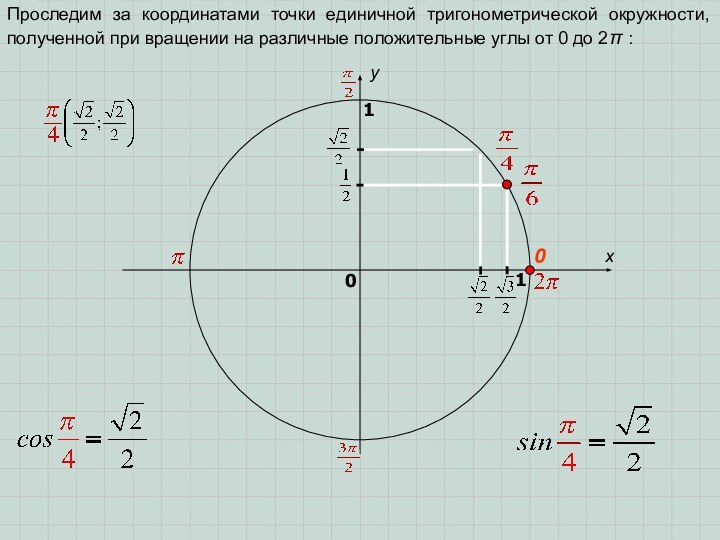
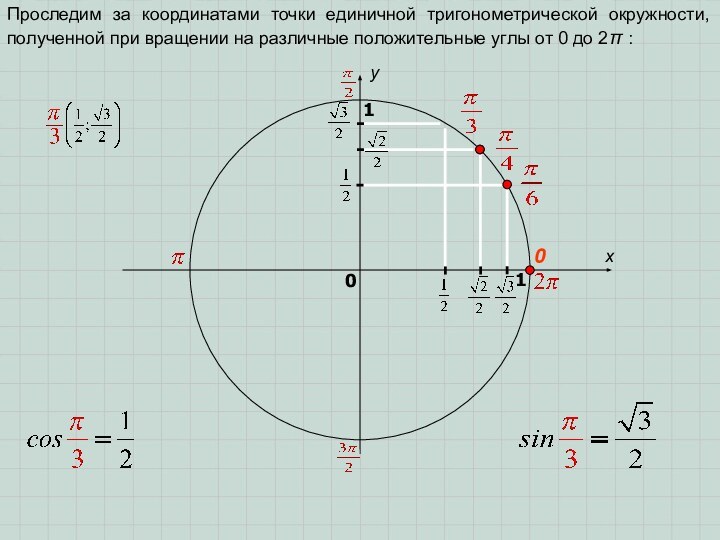
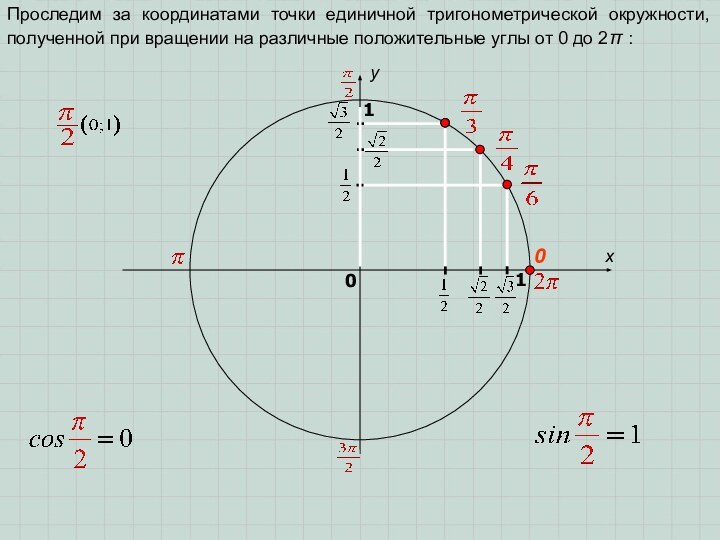
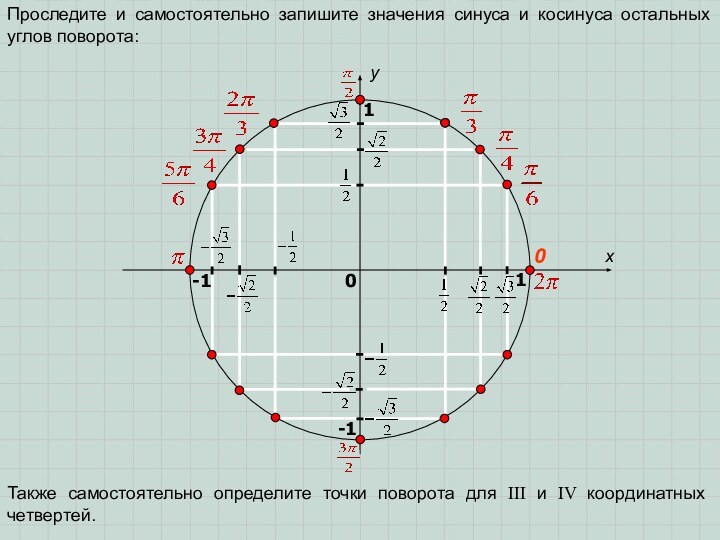
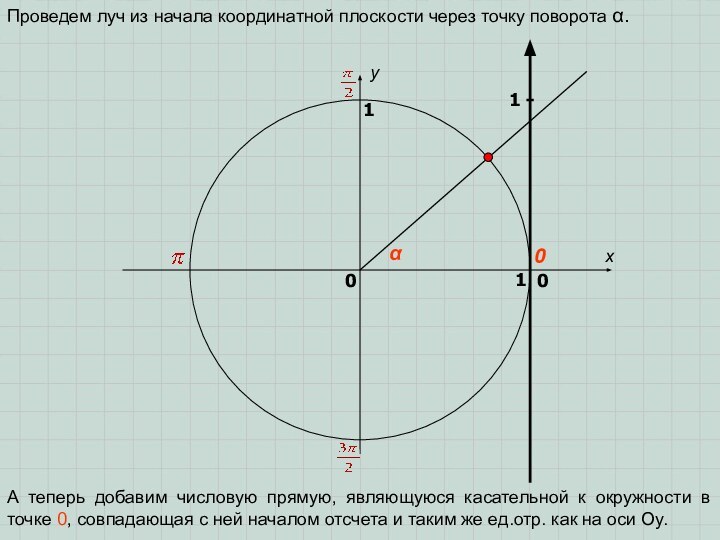
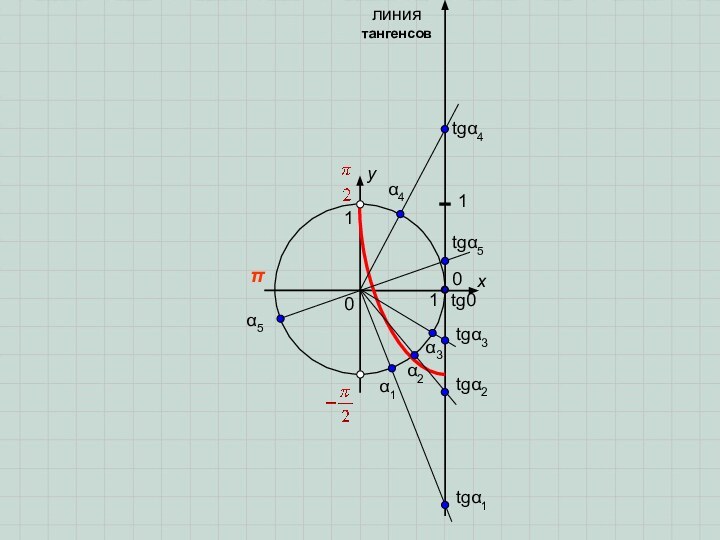
M(x; y)
(x; y) – координаты точки M
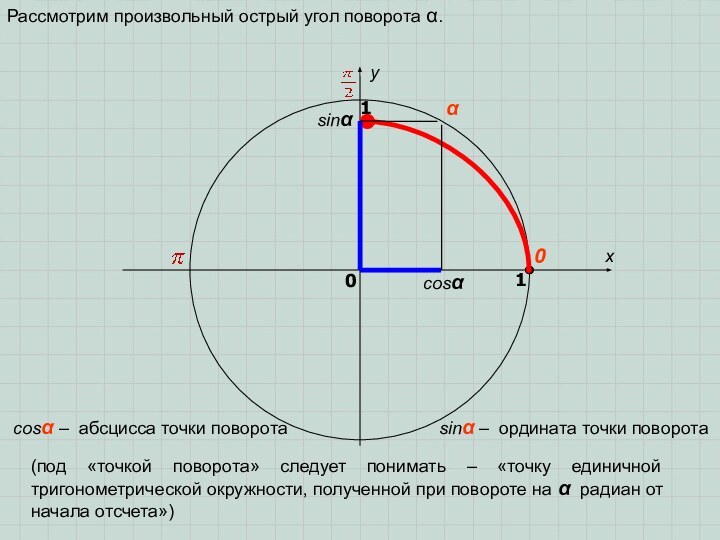
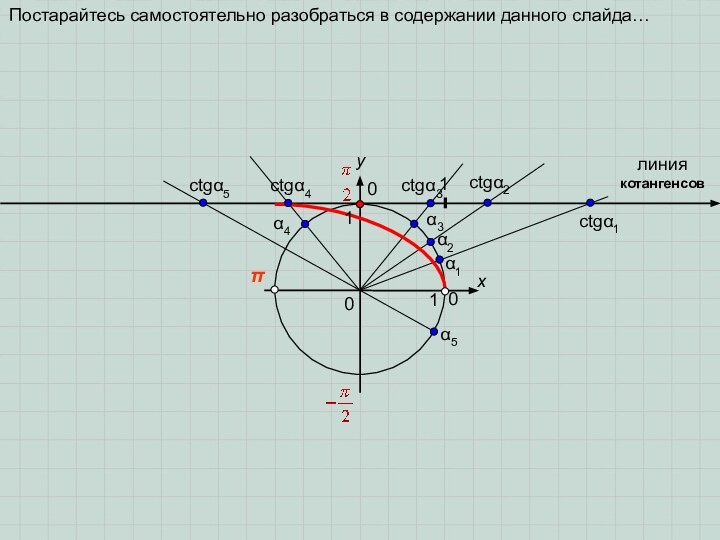
Рассмотрим произвольный острый угол поворота α.
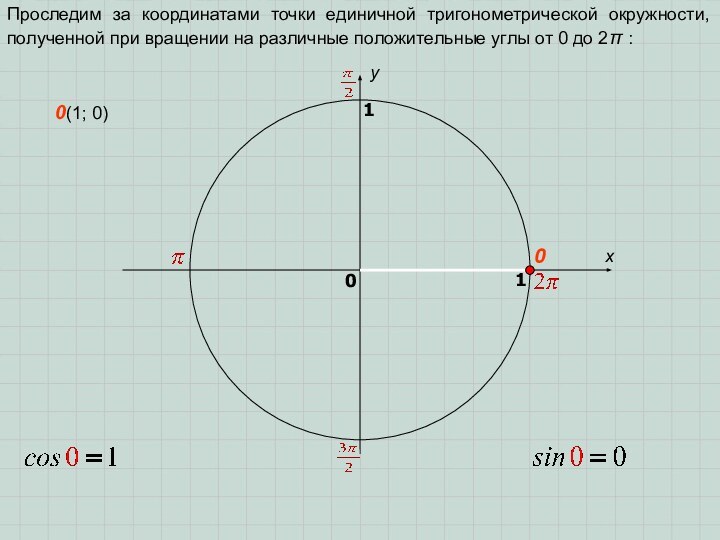
0(1; 0)
1
0
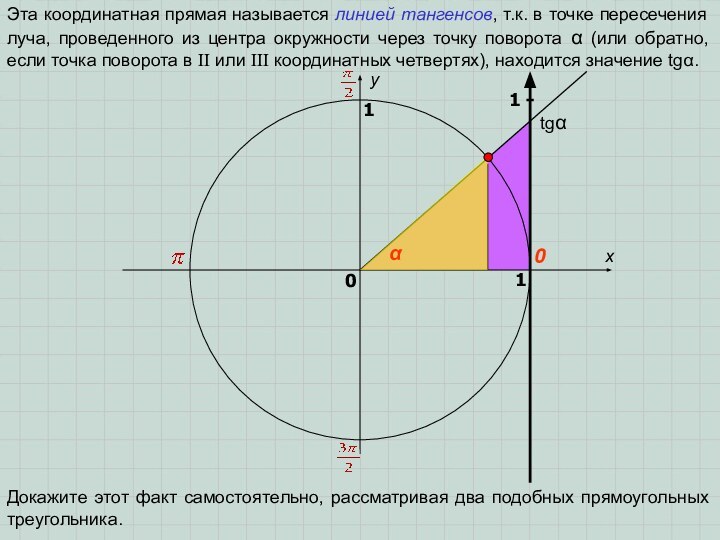
Докажите этот факт самостоятельно, рассматривая два подобных прямоугольных треугольника.
1
tgα
α