Слайд 2
Цель проекта:
изучить одну из кривых второго порядка (параболу)
и сферы её применения.
Задачи проекта :
1.Дать математическое определение параболы.
2.
Изучить свойства параболы.
3. Выяснить, почему параболу называют коническим сечением.
4.Найти сведения о «родственниках» параболы
5. Выявить области применения параболы
Слайд 3
Всем нам хорошо знаком квадратный трехчлен, про который
казалось
бы, мы все знаем: и как корни находить, и
как график строить, и как неравенства квадратичные решать...
Но это поспешное суждение - у нашего старого знакомого есть немало секретов и сюрпризов!
Слайд 4
Пара́бола (греч. παραβολή — приложение) —кривая, точки которой
одинаково удалены от некоторой точки, называемой фокусом, и от
некоторой прямой, называемой директрисой параболы.
Парабола - это сечение конуса плоскостью, параллельной его образующей.
Слайд 5
Еще один способ построения
Оказывается, что парабола – график
квадратичной функции – обладает интересным свойством: есть такая точка и
такая прямая, что каждая точка параболы одинаково удалена от этой точки и от этой прямой (точку называют фокусом параболы, а прямую – директрисой). Это свойство параболы было известно еще математикам античной Греции. Для графика функции у = х2 фокусом служит точка с координатами (0;0,25), а директрисой – прямая у = -0,25.
Попробуйте придумать, как можно строить параболу, используя это свойство.
Слайд 6
Для того чтобы нарисовать параболу, потребуются линейка, угольник,
нить длиной, равной большему катету угольника, и кнопки. Прикрепим
один конец нити к фокусу, а другой - к вершине меньшего угла угольника. Приложим линейку к директрисе и поставим на нее угольник меньшим катетом. Карандашом натянем нить так, чтобы его острие касалось бумаги и прижималось к большему катету. Будем перемещать угольник и прижимать к его катету карандаш так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать на бумаге параболу.
Слайд 7
Свойства параболы
1. Парабола — кривая второго порядка.
2. Она
имеет ось симметрии, называемой осью параболы. Ось проходит через
фокус и вершину перпендикулярно директрисе.
3.Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
4. Для параболы фокус находится в точке (0; 0.25).
Для параболы фокус находится в точке (0; f).
5.Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
Слайд 8
Самые близкие родственники параболы – это окружность, гипербола и эллипс.
А роднит все
эти кривые обыкновенный конус :
провести плоскость, которая параллельна оси конуса,
то линией пересечения окажется гипербола
Слайд 9
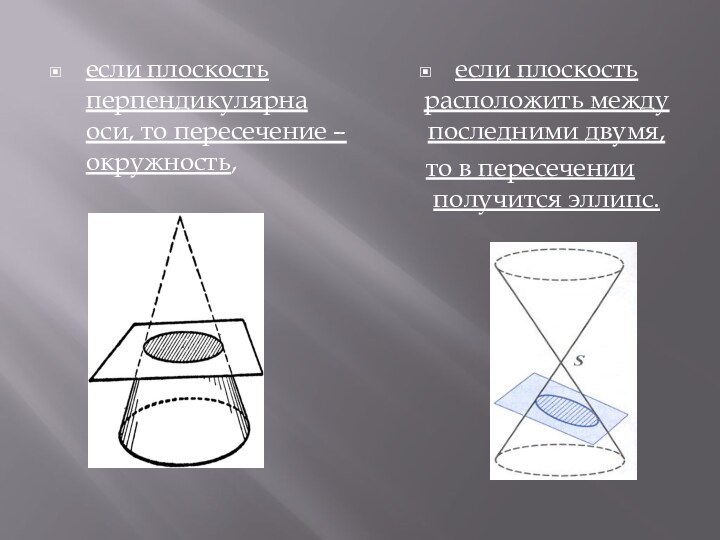
если плоскость перпендикулярна оси, то пересечение – окружность,
если
плоскость расположить между последними двумя,
то в пересечении получится эллипс.
Слайд 10
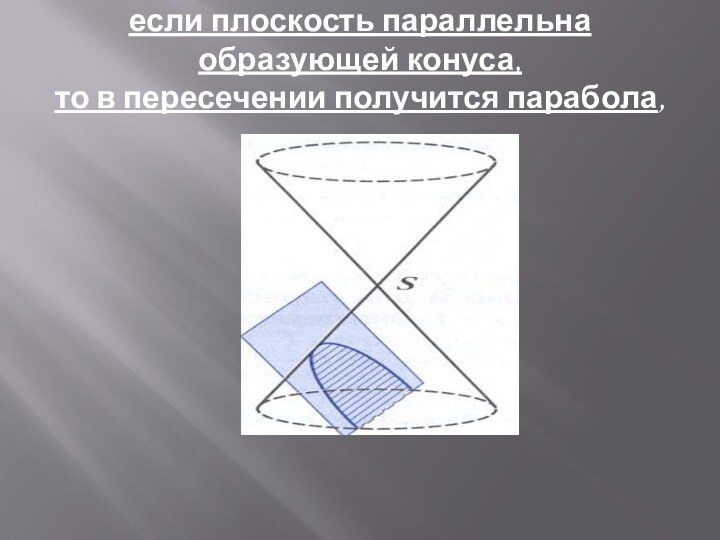
если плоскость параллельна образующей конуса,
то в пересечении получится
парабола,
Слайд 11
Поэтому все эти кривые вместе называют коническими сечениями.
Уже в
340 году до нашей эры греческий математик Менехм знал
о таком свойстве этих кривых, а во втором веке до нашей эры Аполлоний из Перги написал подобный трактат «Конические сечения».
Слайд 12
Циклоида.
Еще одна знаменитая родственница параболы - циклоида. Это траектория
точки обода колеса, которое катится без скольжения по прямой.
Такое название дал кривой Галилей. Если спускаться на санках с горки построенной в виде циклоиды, то время спуска не зависит от того, с какого места начали катиться санки. Но зато спуск с той же высоты по горке любой другой формы займет больше времени. Из-за этого свойства циклоиду еще называют «брахистохроной» (от греческих слов, означающих «кратчайший» и «время»).
Слайд 13
Заметим еще, что касательная к циклоиде в точке
А всегда проходит через верхнюю точку Т производящей окружности.
Именно по этой касательной летит грязь с колеса на спину велосипедиста, если колесо не закрыто крылом.
Слайд 14
Параболоид вращения.
Если вращать параболу вокруг ее оси вращения
то получится поверхность, которую называют параболоидом вращения.
Если сильно размешать
ложечкой воду в стакане, а потом вынуть ложечку, то поверхность воды примет форму такого параболоида.
Слайд 15
Параболоид вращения фокусирует пучок лучей, параллельный главной оси,
в одну точку.
Часто используется свойство параболоида вращения собирать пучок
лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника.
На этом принципе основаны параболические антенны, телескопы-рефлекторы, прожекторы, автомобильные фары.
Использование параболоидов в технике
Слайд 16
Использование параболоидов
в технике
Телескопы-рефлекторы
Прожектор
Автомобильные фары
Слайд 17
Солнечная зажигалка
Оригинальный способ использования энергии Солнца. Солнечная зажигалка
представляет собой параболическое зеркало из нержавеющей стали, почти такое
же, как то, которое используется для зажигания Олимпийского огня в Афинах.
Параболическое зеркало дает возможность собрать всю энергию в одной фокусной точке и зажечь огонь. Температура в этой точке может достигать 537-ми градусов по Цельсию. Такое устройство будет незаменимо в походе и в других полевых условиях.
Слайд 18
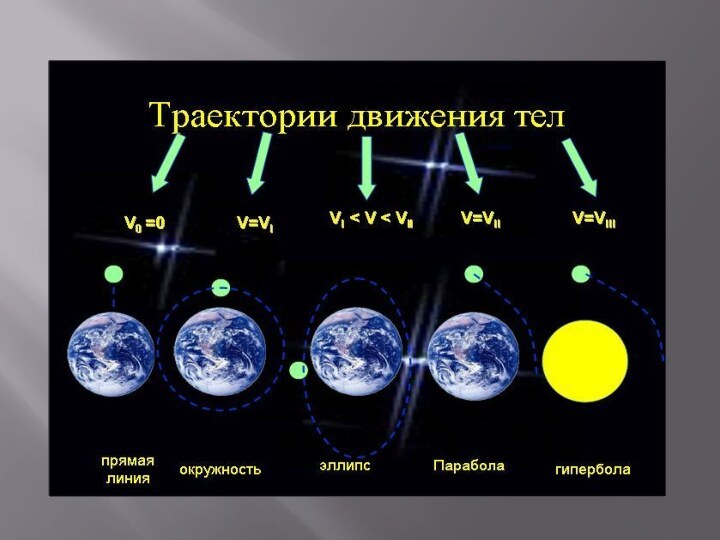
Параболическая орбита и движение спутника по ней
Параболы
в физическом пространстве
Слайд 20
Падение баскетбольного мяча
Параболическая солнечная электростанция в Калифорнии, США.
Слайд 21
Парабола. Её форма невероятна, как, впрочем, и высота.
Некоторые люди
до сих пор не верят в существование этой
странной скалы. Так и говорят:
“Нет ни бога, ни Параболы. А то, что показывают – это фотошоп.”
Парабола в природе
Слайд 23
Параболические траектории струй воды
Слайд 24
Парабола в живой природе
Несомненно заблуждается тот, кто считает,
что параболу можно встретить только на страницах учебника. Внимательно
посмотрите на рисунки и найдите в них параболы.
Сами выполните несколько рисунков листьев, цветов,животных и найдите в них параболы.
Слайд 25
Параболы в животном мире
Траектории прыжков животных близки к
параболе
Слайд 27
Итоги
В ходе работы над данным проектом:
1. Сформулировано строгое
математическое определение параболы.
2. Рассмотрен способ построения параболы.
3. Изучены некоторые
свойства параболы.
4. Выявлена связь между понятиями «парабола» и «конические сечения», найдены родственники параболы.
5. Определены сферы применения параболы(физика, техника, астрономия, архитектура и др.).
6. Подтверждена значимость математики в окружающем мире.