Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Параллельность плоскостей в пространстве. Параллельное проецирование. Площадь ортогональной проекции

Содержание

Параллельные плоскости в пространствеОпределение. Две плоскости в пространстве называются параллельными, если они не пересекаются, то есть не имеют общих точекαIIβ
Параллельность плоскостей в пространстве. Параллельное проецирование. Площадь ортогональной проекции Параллельные плоскости в пространствеОпределение. Две плоскости в пространстве называются параллельными, если Признак параллельности плоскостейТеорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум Свойства параллельных плоскостей1. Если две параллельные плоскости пересекаются третьей плоскостью, то линии их пересечения параллельны.αβ 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.АВ = СDβα Обычно для изображения пространственных фигур на плоскости используется параллельное проектирование пространственной фигуры на плоскость. Пусть π - некоторая плоскость, l - пересекающая ее прямая. Через произвольную Свойства параллельного проектированияЕсли прямая параллельна или совпадает с прямой l, то ее 3. Если две параллельные прямые не параллельны прямой l, то их проекциями Если прямые параллельны, то они проектируются или в две параллельные прямые (рис.1), 4. Отношение отрезков одной прямой или параллельных прямых сохраняется.Середина отрезка АВ переходит Изображение плоских фигур.Треугольник: Изображением треугольника (равнобедренного, равностороннего, прямоугольного, произвольного) 2. Параллелограмма: Изображением любого параллелограмма (параллелограмма, прямоугольника, квадрата и 3. Трапеции: Изображением любой трапеции (равнобокой, прямоугольной, произвольной) на 4. Окружность: Проекцией окружности является эллипс. Проекция центра окружности называется центром эллипса Ортогональным проектированием называется параллельное проектирование в направлении прямой, перпендикулярной плоскости проектирования.Ортогональное проектированиеДля Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту Теорема. Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной Даны параллельные плоскости α и β. Через точки Р и Н плоскости Точка В не лежит в плоскости треугольника ADC, точки М, N и Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно в Дан равносторонний треугольник со стороной а. Найдите площадь его ортогональной проекции на
Слайды презентации

Слайд 2 Параллельные плоскости в пространстве
Определение. Две плоскости в

Параллельные плоскости в пространствеОпределение. Две плоскости в пространстве называются параллельными, если

пространстве называются параллельными, если они не пересекаются, то есть

не имеют общих точек

αIIβ

Слайд 3 Признак параллельности плоскостей
Теорема. Если две пересекающиеся прямые одной

Признак параллельности плоскостейТеорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны

плоскости соответственно параллельны двум прямым другой плоскости, то эти

плоскости параллельны.

Слайд 4 Свойства параллельных плоскостей
1. Если две параллельные плоскости пересекаются

Свойства параллельных плоскостей1. Если две параллельные плоскости пересекаются третьей плоскостью, то линии их пересечения параллельны.αβ

третьей плоскостью, то линии их пересечения параллельны.
α
β

Слайд 5 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями,

2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.АВ = СDβα

равны.
АВ = СD
β
α

Слайд 6 Обычно для изображения пространственных фигур на плоскости используется

Обычно для изображения пространственных фигур на плоскости используется параллельное проектирование пространственной фигуры на плоскость.

параллельное проектирование пространственной фигуры на плоскость.

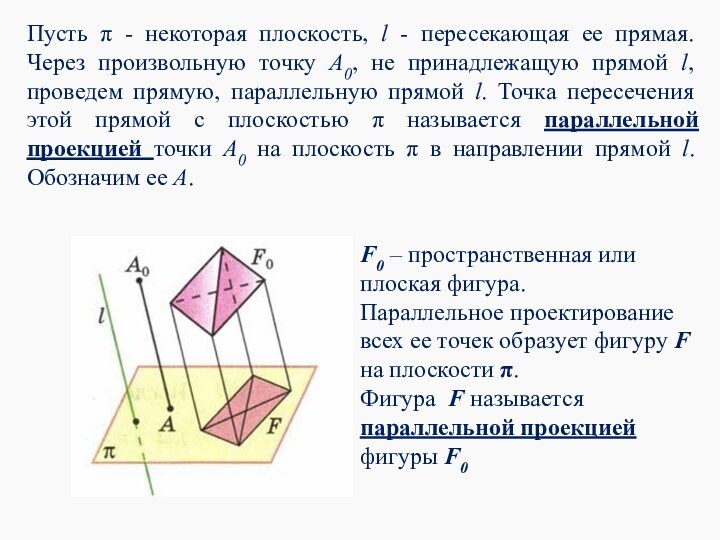
Слайд 7 Пусть π - некоторая плоскость, l - пересекающая

Пусть π - некоторая плоскость, l - пересекающая ее прямая. Через

ее прямая. Через произвольную точку A0, не принадлежащую прямой

l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью π называется параллельной проекцией точки A0 на плоскость π в направлении прямой l. Обозначим ее A.

F0 – пространственная или плоская фигура.
Параллельное проектирование всех ее точек образует фигуру F на плоскости π.
Фигура F называется параллельной проекцией фигуры F0

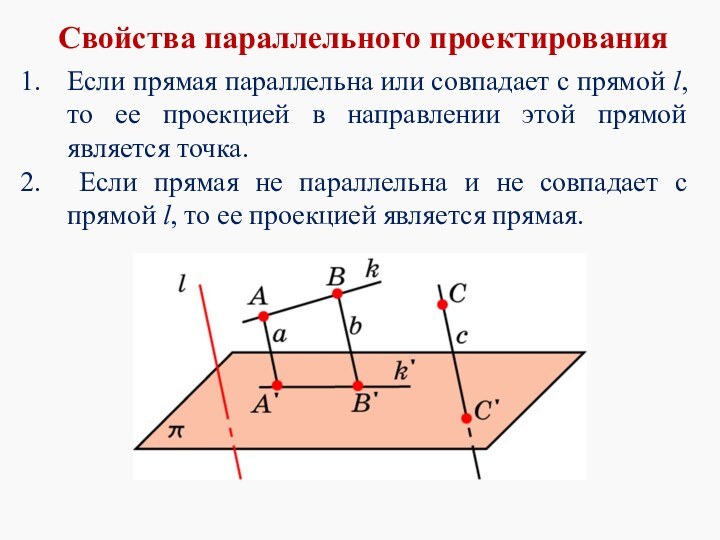
Слайд 8 Свойства параллельного проектирования
Если прямая параллельна или совпадает с

Свойства параллельного проектированияЕсли прямая параллельна или совпадает с прямой l, то

прямой l, то ее проекцией в направлении этой прямой

является точка.
Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.

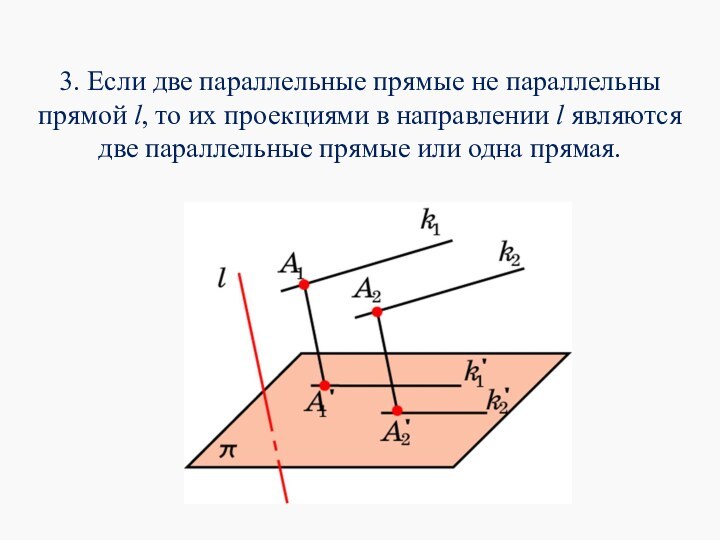
Слайд 9 3. Если две параллельные прямые не параллельны прямой

3. Если две параллельные прямые не параллельны прямой l, то их

l, то их проекциями в направлении l являются две

параллельные прямые или одна прямая.

Слайд 10 Если прямые параллельны, то они проектируются или в

Если прямые параллельны, то они проектируются или в две параллельные прямые

две параллельные прямые (рис.1), или в одну прямую (их

плоскость параллельна направлению проектирования, но сами они не параллельны направлению проектирования) (рис. 2), или в две точки (прямые параллельны направлению проектирования) (рис.3)

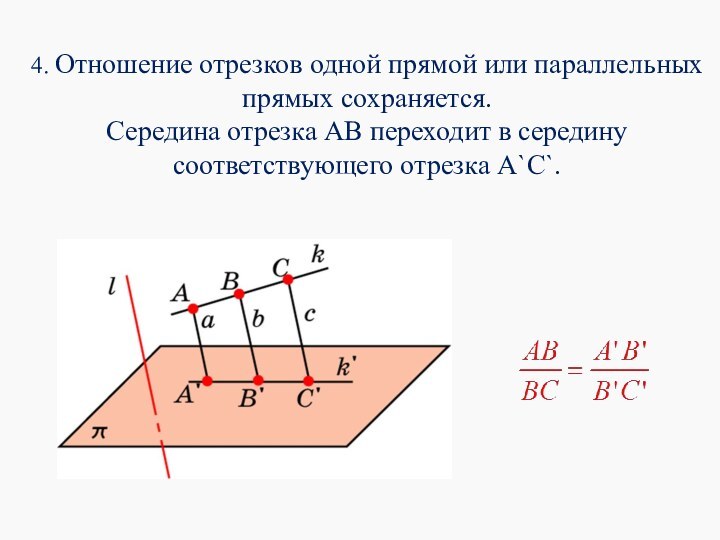
Слайд 11 4. Отношение отрезков одной прямой или параллельных прямых

4. Отношение отрезков одной прямой или параллельных прямых сохраняется.Середина отрезка АВ

сохраняется.
Середина отрезка АВ переходит в середину соответствующего отрезка А`C`.


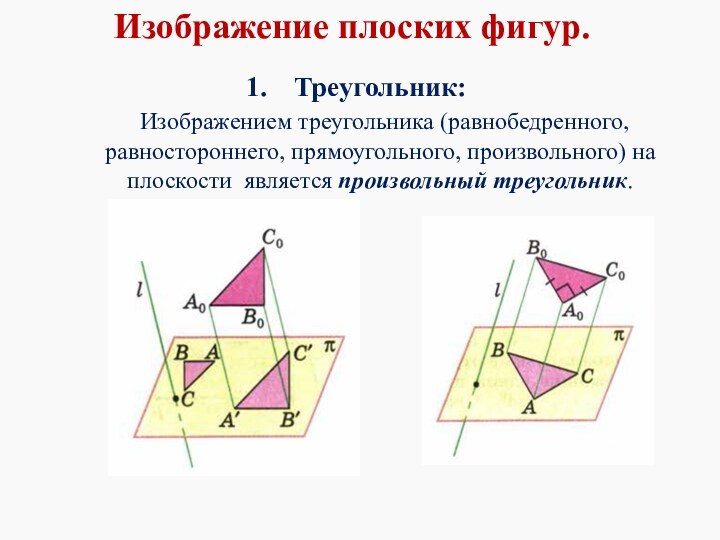
Слайд 12 Изображение плоских фигур.
Треугольник:
Изображением треугольника

Изображение плоских фигур.Треугольник: Изображением треугольника (равнобедренного, равностороннего, прямоугольного, произвольного) на плоскости является произвольный треугольник.

(равнобедренного, равностороннего, прямоугольного, произвольного) на плоскости является произвольный треугольник.

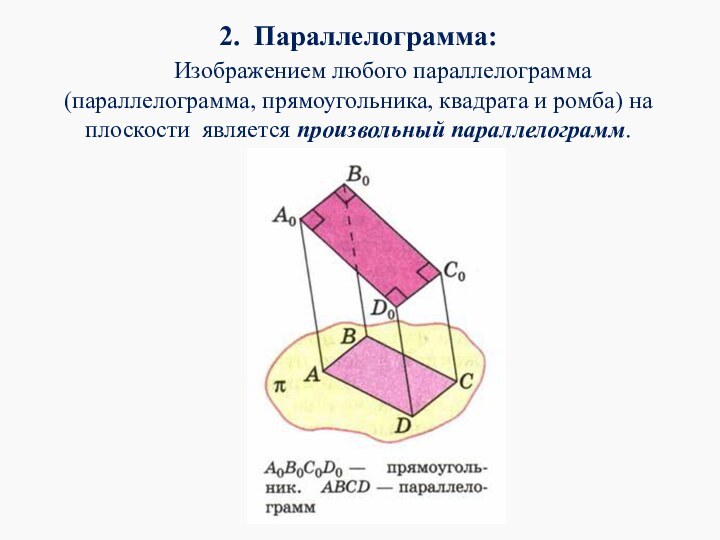
Слайд 13 2. Параллелограмма:
Изображением любого параллелограмма

2. Параллелограмма: Изображением любого параллелограмма (параллелограмма, прямоугольника, квадрата и ромба) на плоскости является произвольный параллелограмм.

(параллелограмма, прямоугольника, квадрата и ромба) на плоскости является произвольный

параллелограмм.

Слайд 14 3. Трапеции:
Изображением любой трапеции

3. Трапеции: Изображением любой трапеции (равнобокой, прямоугольной, произвольной) на плоскости

(равнобокой, прямоугольной, произвольной) на плоскости является произвольная трапеция, у

которой отношение оснований равно отношению оснований данной трапеции

Слайд 15 4. Окружность:
Проекцией окружности является

4. Окружность: Проекцией окружности является эллипс. Проекция центра окружности называется центром эллипса

эллипс.
Проекция центра окружности называется центром эллипса

Слайд 16 Ортогональным проектированием называется параллельное проектирование в направлении прямой,

Ортогональным проектированием называется параллельное проектирование в направлении прямой, перпендикулярной плоскости проектирования.Ортогональное

перпендикулярной плоскости проектирования.
Ортогональное проектирование
Для ортогонального проектирования справедливы свойства параллельного

проектирования.

Слайд 17 Ортогональной проекцией точки А на данную плоскость называется

Ортогональной проекцией точки А на данную плоскость называется проекция точки на

проекция точки на эту плоскость параллельно прямой, перпендикулярной этой

плоскости..

Ортогональная проекция точки и фигуры

Ортогональная проекция фигуры на данную плоскость π состоит из ортогональных проекций на плоскость π всех точек этой фигуры

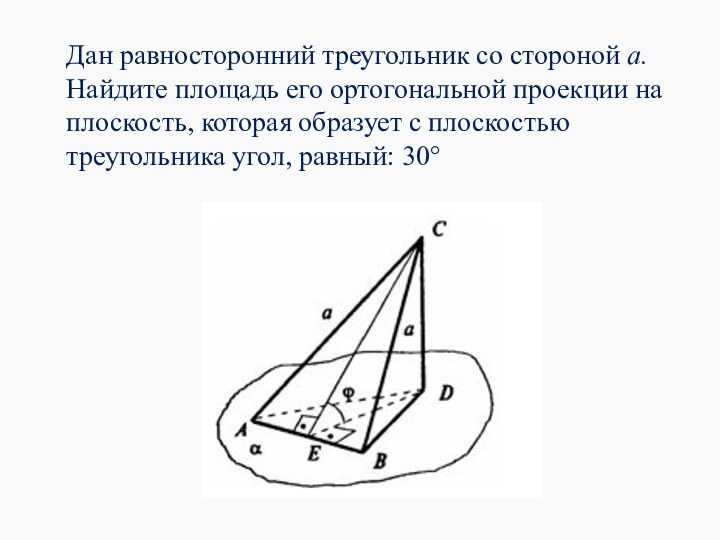
Слайд 18 Теорема. Площадь ортогональной проекции многоугольника на плоскость равна

Теорема. Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника,

площади проектируемого многоугольника, умноженной на косинус угла, образованного плоскостью

многоугольника и плоскостью проекции.

SАBD= SABC* cosφ

Площадь ортогональной проекции

Слайд 19

Слайд 20 Даны параллельные плоскости α и β. Через точки

Даны параллельные плоскости α и β. Через точки Р и Н

Р и Н плоскости α проведены параллельные прямые, пересекающие

плоскость β в точках С и К. Найдите РС, если НК = 20 см.

Слайд 21 Точка В не лежит в плоскости треугольника ADC,

Точка В не лежит в плоскости треугольника ADC, точки М, N

точки М, N и Р — середины отрезков ВА,

ВС и BD соответственно.
а) Докажите, что плоскости MNP и ADC параллельны.
б) Найдите площадь треугольника MNP, если площадь треуголь­ника ADC равна 48 см2.

Слайд 22 Параллельные плоскости α и β пересекают сторону АВ

Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно

угла ВАС соответственно в точках А1 и А2 ,

а сторону АС этого уг­ла — соответственно в точках В1 , и В2.
Найдите:
АА2 и АВ2, если А1А2 = 2А1А = 12 см,
АВ, = 5 см;
  • Имя файла: parallelnost-ploskostey-v-prostranstve-parallelnoe-proetsirovanie-ploshchad-ortogonalnoy-proektsii.pptx
  • Количество просмотров: 122
  • Количество скачиваний: 0
- Предыдущая Фирменный стиль. Разработка логотипа для частной компании Суши тайм
Следующая - Периодизация психологического развития

Похожие презентации

Презентация по математике на тему Решение линейных неравенств с одной переменной (6 класс) Презентация по математике на тему Решение линейных неравенств с одной переменной (6 класс) 115
Решение уравнений на нахождение неизвестного уменьшаемого Решение уравнений на нахождение неизвестного уменьшаемого 130
Признак перпендикулярности прямой и плоскости Признак перпендикулярности прямой и плоскости 160
Презентация по математике Умножение натуральных чисел. Законы умножения (5 класс) Презентация по математике Умножение натуральных чисел. Законы умножения (5 класс) 154
Презентация по математике Таблица умножения 3 к ласс Презентация по математике Таблица умножения 3 к ласс 132
Применение графов в теории вероятностей Применение графов в теории вероятностей 136
Графики функций Графики функций 133
Простые и сложные проценты Простые и сложные проценты 222
Презентация по математике Математика и факты 10-11 классы Презентация по математике Математика и факты 10-11 классы 157
Презентация к интегрированному уроку по математике и географии Рациональные числа в рельефе Земли Презентация к интегрированному уроку по математике и географии Рациональные числа в рельефе Земли 111
Презентация к уроку на тему Упрощение выражений Презентация к уроку на тему Упрощение выражений 151
Параллельность прямых в пространстве Параллельность прямых в пространстве 114
Интерактивный тренажёр Примеры на все действия Интерактивный тренажёр Примеры на все действия 102
Презентация по математике Сложение и вычитание чисел. презентация к уроку по математике (1 класс) Презентация по математике Сложение и вычитание чисел. презентация к уроку по математике (1 класс) 183
Презентация к уроку математики в 3 классе ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ЗАДАЧИ НА ПОСТРОЕНИЕ СИММЕТРИЧНЫХ ФИГУР, школа 21 века. презентация к уроку по математике (3 класс) Презентация к уроку математики в 3 классе ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ЗАДАЧИ НА ПОСТРОЕНИЕ СИММЕТРИЧНЫХ ФИГУР, школа 21 века. презентация к уроку по математике (3 класс) 181
6-prezentaciya1 6-prezentaciya1 130
Презентация по математике на тему Закрепление изученного.Числа от 11 до 20 Презентация по математике на тему Закрепление изученного.Числа от 11 до 20 98
Целые уравнения и способы их решения Целые уравнения и способы их решения 107
Презентация к уроку десятичные дроби Презентация к уроку десятичные дроби 129
Геометрия Лобачевского Геометрия Лобачевского 125
Использование ИКТ презентация к уроку по математике (3 класс) Использование ИКТ презентация к уроку по математике (3 класс) 100
Урок закрепления 4 класс презентация к уроку по математике (4 класс) Урок закрепления 4 класс презентация к уроку по математике (4 класс) 123
Конспект непосредственно образовательной деятельности по формированию элементарных математических представлений у детей второй младшей группы Тема Волшебный паровоз план-конспект занятия по математике (младшая группа) Конспект непосредственно образовательной деятельности по формированию элементарных математических представлений у детей второй младшей группы Тема Волшебный паровоз план-конспект занятия по математике (младшая группа) 130
Программа подготовки к ГИА по математике Программа подготовки к ГИА по математике 102
Презентация к уроку № 6 по математике для 6 класса Презентация к уроку № 6 по математике для 6 класса 113
презентация к занятию по ФЭМП в средней группе презентация к уроку по математике (средняя группа) презентация к занятию по ФЭМП в средней группе презентация к уроку по математике (средняя группа) 116
Решение экономических задач в рамках ЕГЭ Решение экономических задач в рамках ЕГЭ 118
Презентация к уроку математики в 1 классе по теме Многоугольники по программе Начальная школа ХХI века презентация к уроку по математике (1 класс) Презентация к уроку математики в 1 классе по теме Многоугольники по программе Начальная школа ХХI века презентация к уроку по математике (1 класс) 119
Приёмы устного решения квадратного уравнения 8 класс Приёмы устного решения квадратного уравнения 8 класс 98
Курсовая работа по дисциплине “Математические методы” на тему “Игры с природой” Курсовая работа по дисциплине “Математические методы” на тему “Игры с природой” 117