к двум пересекающимся прямым, лежащим в плоскости, то она
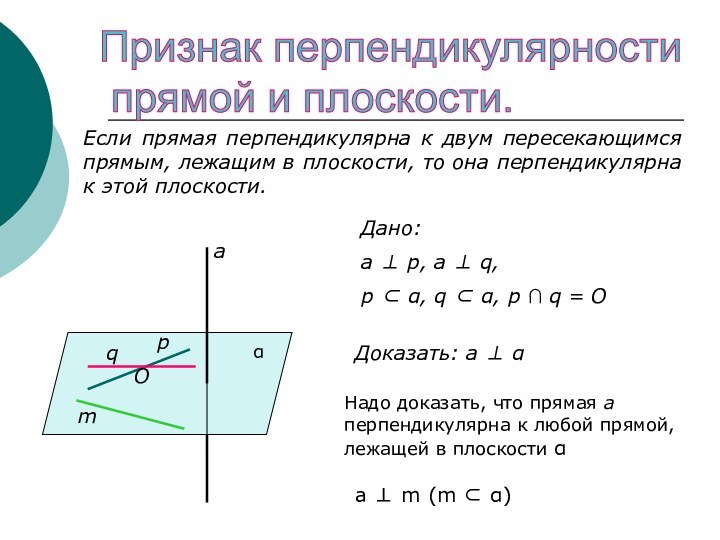
перпендикулярна к этой плоскости.Дано:
а ⊥ р, а ⊥ q,
p ⊂ α, q ⊂ α, p ∩ q = O
Доказать: а ⊥ α
Надо доказать, что прямая а перпендикулярна к любой прямой, лежащей в плоскости α
а
p
q
О
m
α
a ⊥ m (m ⊂ α)