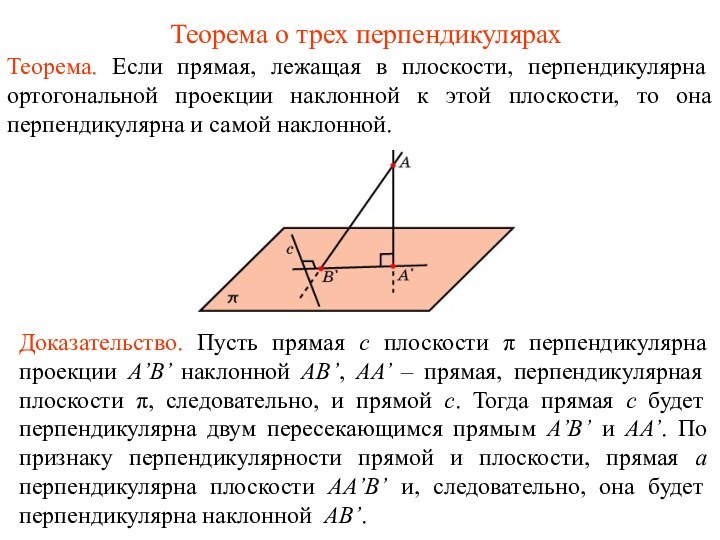
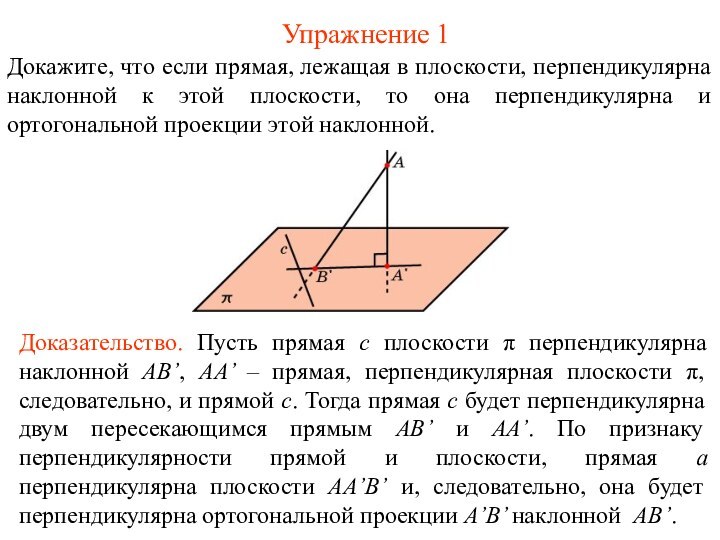
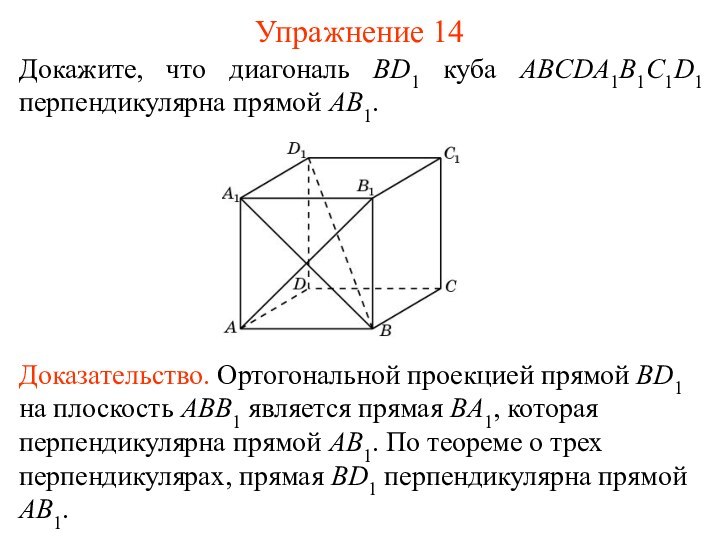
плоскости, перпендикулярна ортогональной проекции наклонной к этой плоскости, то
она перпендикулярна и самой наклонной.Доказательство. Пусть прямая c плоскости π перпендикулярна проекции A’B’ наклонной AB’, AA’ – прямая, перпендикулярная плоскости π, следовательно, и прямой c. Тогда прямая c будет перпендикулярна двум пересекающимся прямым A’B’ и AA’. По признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости АA’В’ и, следовательно, она будет перпендикулярна наклонной АВ’.