Слайд 2
Структура дисциплины
Лекции – 32 ч.
Практические занятия – 32 ч.
ОТЧЕТНОСТЬ
Контрольная работа - 5
ТЕСТЫ - 1
ФОРУМ - 1
Экзамен
Слайд 3
ВВЕДЕНИЕ В ИССЛЕДОВАНИЕ ОПЕРАЦИЙ
Исследование операций — научная дисциплина,
занимающаяся разработкой и практическим применением методов наиболее эффективного управления
различными организационными системами.
Операция — любое управляемое мероприятие, направленное на достижение цели.
Оптимальными считают те решения, которые по тем или иным соображениям предпочтительнее других.
Слайд 4
ЭТАПЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
1. Постановка задачи.
2. Построение содержательной модели
рассматриваемого объекта.
3. Построение математической модели.
4. Анализ модели или получение
решения задачи.
5. Анализ решения
6. Проверка полученных результатов на их адекватность природе изучаемой системы.
Слайд 5
Лекция 1.
Экономико-математическая модель (ЭММ). Понятие, пример, общая классификация
ЭММ.
Общая задача линейного программирования, основные элементы и понятия.
Общая
запись оптимизационной ЭММ (задача оптимального программирования). Основные элементы и понятия.
Графический метод решения задачи линейного программирования.
Особые случаи решения ЗЛП графическим методом.
Каноническая форма записи ЗЛП. Способы приведения ЗЛП к каноническому виду
Экономический смысл основных и дополнительных переменных в канонической форме задачи об оптимальном использовании ограниченных ресурсов
Слайд 6
Математический аппарат линейного программирования
Понятие о выпуклых множествах
Множество – определенная сово-
купность объектов (элементов)
Различают множества:
- выпуклые;
- невыпуклые.
Слайд 7
Множество выпукло, если вместе
с его любыми двумя точками ему принадлежит и весь
отрезок их соединяющий.
Множество невыпукло, если существует хотя бы одна такая пара точек множества, что отрезок, соединяющий эти точки не принадлежит целиком этому множеству.
а
в
c
d
Слайд 8
Понятие угловой точки
Для выпуклых множеств вводится поня-тие угловой
точки.
Угловой (крайней) точкой выпуклого множества называется точка, через которую
нельзя провести ни одного отрезка состоящего только из точек данного множества, для которого она была бы внутренней.
угловая
внутренняя точка
точка
Слайд 9
Пример 1. Задача оптимального использования ресурсов (задача
о коврах)
В распоряжении фабрики имеется определенное количество ресурсов: рабочая
сила, деньги, сырье, оборудование, производственные площади и т.п. Например, пусть это будут ресурсы трех видов: рабочая сила (80 чел./дней), сырье (480 кг пряжи) и оборудование (130 станкочасов). Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса, необходимых для производства одного ковра каждого вида и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в табл.1.
Требуется найти такой план выпуска продукции, при котором общая стоимость продукции будет максимальной.
Слайд 11
Экономико-математическая модель задачи
Переменные
Обозначим через X1, X2, X3, X4
количество ковров каждого типа.
Целевая функция – это выражение,
которое необходимо максимизировать:
F(x)= 3X1 +4 X 2 +3 X 3 + X 4 .
Функциональные ограничения (ограничения по ресурсам)
7x1 +2x2 +2x3 +6x4 ≤80 (человеко/дней),
5x1 +8x2 +4x3 +3x4≤480 (кг пряжи),
2x1 +4x2 +x3 + 8x4 ≤ 130 (станкочасов),
Прямые ограничения x1, x2, x3, x4≥0.
Слайд 12
Пример 2.
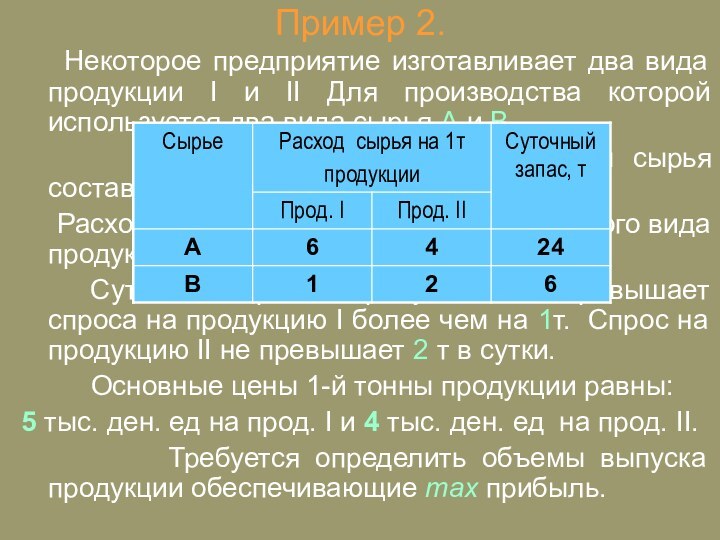
Некоторое предприятие изготавливает два
вида продукции I и II Для производства которой используется
два вида сырья A и B.
Максимальные суточные запасы сырья составляют 24 и 6 тонн соответственно.
Расходы на производство 1-й тонны каждого вида продукции приведены в таблице.
Суточный спрос на продукцию II не превышает спроса на продукцию I более чем на 1т. Спрос на продукцию II не превышает 2 т в сутки.
Основные цены 1-й тонны продукции равны:
5 тыс. ден. ед на прод. I и 4 тыс. ден. ед на прод. II.
Требуется определить объемы выпуска продукции обеспечивающие max прибыль.
Слайд 13
Составим ЭММ задачи по следующей схеме
1. Идентифицируем переменные;
2.
Выявим цель задачи, для дости-жения которой из всех допустимых
значений перемененных нужно выбрать такое сочетание, которое будет соответствовать оптимальному решению;
3. Выявим ограничения, которые будут наложены на переменные.
Далее реализуем приведенную схему.
Слайд 14
1. Поскольку в условии задачи требуется определить объемы
производства каждо-го вида продукции, то обозначим иском-ые переменные через
x1 и x2:
x1 – суточный объем производства продук-ции первого вида (т);
x2 – суточный объем производства продук-ции второго вида (т).
2. Составим целевую функцию задачи.
Прибыль предприятия будет складывать-ся в виде суммы прибылей от реализации продукции первого и второго вида. Запишем это условие.
Слайд 15
F(x) = 5x1 + 4x2 => max
3. Выделим
ограничения:
на расход используемых продуктов
6x1 + 4x2 ≤ 24
- по сырью А,
1x1 + 2x2 ≤ 6 - по сырью В,
-1x1 + 1x2 ≤ 1 - по превышению спроса продукции II над I,
0x1 + 1x2 ≤ 2 - по спросу на продукцию II,
x1 ≥ 0, x2 ≥ 0 - условие неотрицат.
Задачи подобного вида называю ЗЛП.
Слайд 16
Линейное программирование – область математики, разрабатывающая теорию и
численные методы решения задач нахождения экстремума (максимума или минимума)
линейной функции многих переменных при наличии линейных ограничений, т.е. линейных равенств или неравенств, связывающих эти переменные.
Слайд 17
К задачам линейного программирования приводится широкий круг вопросов
планирования экономических и технико-экономических процессов, где ставится задача поиска
наилучшего (оптимального решения), само возникновение и развитие линейного программирования непосредственно связано с экономической проблематикой
Слайд 28
Задача о костюмах
Пример 3. Планирование выпуска продукции пошивочного
предприятия.
Намечается выпуск двух видов костюмов – мужских и женских.
На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм – 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат. Требуется определить, сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского – 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.
Слайд 29
Экономико-математическая модель задачи о костюмах
Переменные: х1 – число
женских костюмов; x2 – число мужских костюмов.
Максимизировать целевую
функцию
f(x) = 10 х1 + 20 х2
Ограничения задачи имеют вид:
х1 + х2 150,
2 х1 + 0,5 х2 240,
х1 + 3,5 х2 350,
х2 60,
х1 0.
Слайд 30
Графический метод решения ЗЛП
Строится многоугольная область допустимых решений
(ОДР) ЗЛП.
Строится вектор-градиент целевой функции (ЦФ) с началом в
точке x0, (0;0)
Линия уровня c1x1+c2x2 = а (а – постоянная величина) – прямая, перпендикулярная вектору-градиенту , – передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
Для нахождения координат точки максимума достаточно решить систему уравнений прямых, дающих в пересечении точку максимума. Значение f(x1,x2), найденное в полученной точке, является максимальным значением целевой функции.
Слайд 31
В качестве примера рассмотрим составленную ранее ЭММ(пример 2):
F(x) = 5x1 + 4x2 => max
6x1 +
4x2 ≤ 24, – (1)
1x1 + 2x2 ≤ 6, – (2)
-1x1 + 1x2 ≤ 1, – (3)
0x1 + 1x2 ≤ 2, – (4)
x1 ≥ 0, – (5)
x2 ≥ 0. – (6)
Затем пронумеруем все ограничения
Слайд 32
Построение ОДР
- проведем оси и обоз-начим их через
x1 и x2;
- на оси нанесем делен-ия;
- учтем условия
неотри-цательности перемен-
ных x1 ≥ 0 и x2 ≥ 0 , это означает, что решение необходимо искать в первой четверти;
- далее каждое неравен-ство поочередно заме-няем на равенство и по ним строим прямые на графике.
Слайд 33
6x1 + 4x2 = 24 –
(1)
6x1 + 4x2 ≤ 24
Строим первую линию ограничения
Слайд 34
6x1 + 4x2 = 24 –
(1)
1x1 + 2x2 = 6 – (2)
О
Д Р
Строим вторую линию ограничения
Слайд 35
Строим третью линию ограничения
6x1 + 4x2 = 24
– (1)
1x1 + 2x2 = 6
– (2)
-1x1 + 1x2 = 1 – (3)
О Д Р
Слайд 36
Строим четвертую линию ограничения
6x1 + 4x2 = 24
– (1)
1x1 + 2x2 = 6
– (2)
-1x1 + 1x2 = 1 – (3)
0x1 + 1x2 = 2 – (4)
О Д Р
Слайд 37
Поиск оптимального решения
Для поиска оптимального решения в ОДР
строим линию уровня и вектор-градиент.
Линия уровня целевой функции –
прямая линия, построенная по уравнению целевой функции, в множестве точек которой целевая функции принимает одно и то же значение.
Вектор-градиент целевой функции – вектор, координаты начала которого совпадают с началом координат, а координатами конца, являются частные производные этой функции, вычисленные в некоторой точке.
Свойство вектора-градиента – указывает направление наиболее быстрого возрастания функции в окрестности выбранной точки и он перпендикулярен линиям уровня.
Алгоритм построения линии уровня:
в ОДР произвольно выбирается точка, с координатами x1 и x2 удобными для вычисления;
координаты выбранной точки подставляются в уравнение целевой функции;
рассчитывается значение целевой функции;
Слайд 38
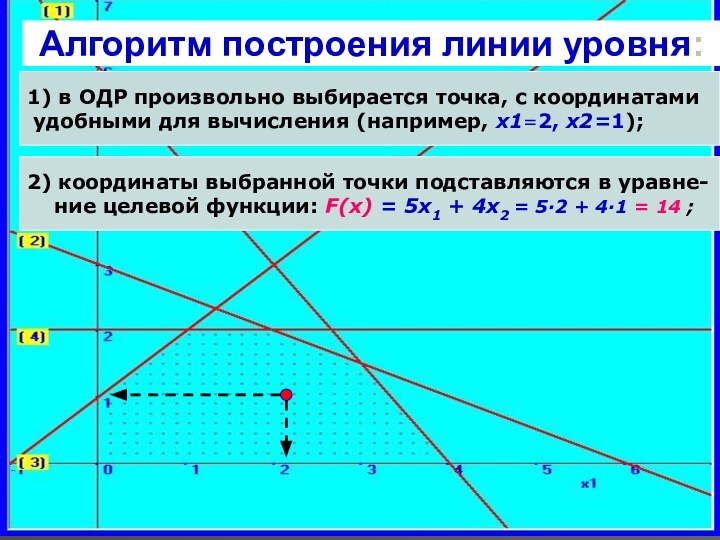
Алгоритм построения линии уровня:
1) в ОДР произвольно выбирается
точка, с координатами
удобными для вычисления (например, x1=2,
x2=1);
2) координаты выбранной точки подставляются в уравне-
ние целевой функции: F(x) = 5x1 + 4x2 = 5·2 + 4·1 = 14 ;
Слайд 39
Алгоритм построения линии уровня:
3) Записывается уравнение целевой функции
5x1 + 4x2 = 14 ;
4) По уравнению целевой
функции F(x) находятся
координаты второй точки для построения линии уровня;
5) Через две точки проводится линия уровня F(x)=14;
Линия уровня F(x)=14
Слайд 40
Построение вектора-градиента
Координатами конца вектора-градиента являются
коэффициенты при переменных
в целевой функции
(5,4)
5x1 + 4x2 = 14 ;
2) Начало вектора-градиента совпадает с началом
координат;
3) Строим вектор-градиент.
Слайд 41
Вектор-градиент
Линия уровня
Оптимум
Слайд 42
В крайней, угловой точке достигается максимум целевой функции.
Для нахождения координат этой точки достаточно решить систему из
двух уравнений прямых, дающих в пересечении точку максимума:
6х1 + 4 х2 = 24,
х1 + 2х2 = 6
Решая систему, получаем х1= 3, х2 = 1.5
Ответ
Для получения максимальной прибыли - 21 тыс. ден. единиц (F(x) = 5x1 + 4x2 =5×3+4×1.5=21) необходимо выпустить 3 тонны первого продукта и полторы тонны второго.
Слайд 43
Особые случаи решения ЗЛП
В процессе решения ЗЛП
могут встретить-ся особые случаи:
Неединственность оптимального решения;
Вырожденность базисного решения;
Отсутствие конечного
оптимума;
Область допустимых решений представлена одной точкой;
Множество допустимых решений пусто.
Слайд 44
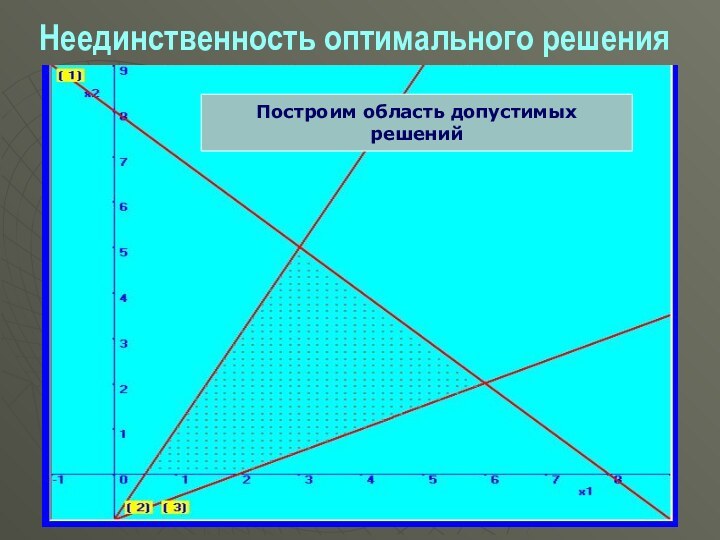
Неединственность оптимального решения
Построим область допустимых решений
Слайд 45
Неединственность оптимального решения
Задача имеет
бесконечное множество
Opt решений, которые задают координаты
точек отрезка AB. Но
среди этих решений
существует два базисных в точках A и B.
A
B
Линия уровня совпадает
с линией ограничений
Здесь коэффициенты при переменных в огран. и в Ц.Ф. пропорциональны.
Слайд 46
Вырожденность базисного решения
Построим область допустимых решений
Слайд 47
Вырожденность базисного решения
A
В т. A пересекаются
три прямых и в этой
точке имеем систему из
трех уравнений с двумя
неизвестными, т.е. одно уравнение избыточно.
Задача становится переопределенной.
Вырожденность вызывает:
- зацикливание в решении;
- появление вырожденного
неоптимального решения.
Слайд 48
Отсутствие конечного оптимума
Построим область допустимых решений
Слайд 49
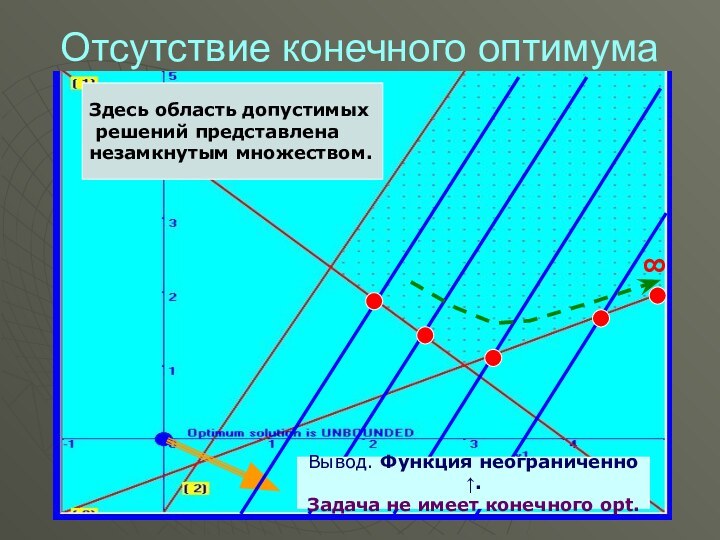
Отсутствие конечного оптимума
Здесь область допустимых
решений представлена
незамкнутым множеством.
Вывод.
Функция неограниченно .
Задача не имеет конечного opt.
∞
Слайд 50
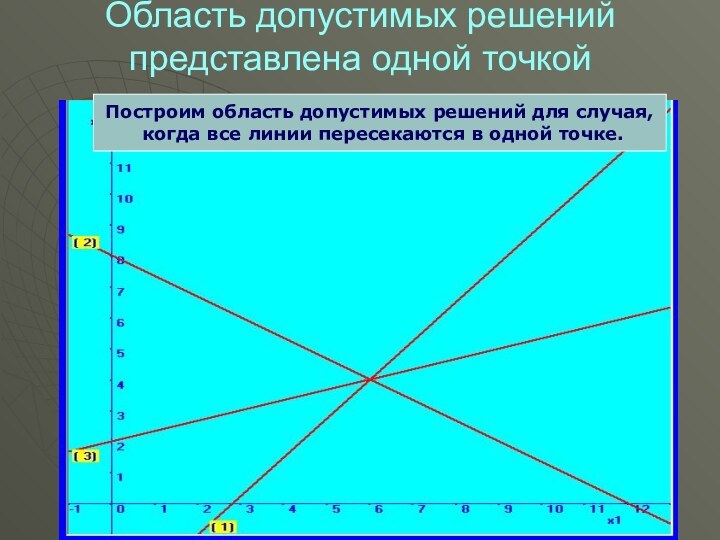
Область допустимых решений представлена одной точкой
Построим область допустимых
решений для случая,
когда все линии пересекаются в одной
точке.
Слайд 51
Область допустимых решений представлена одной точкой
В данном случае
точки максимума и минимума
целевой функции f(x) совпадают.
Слайд 52
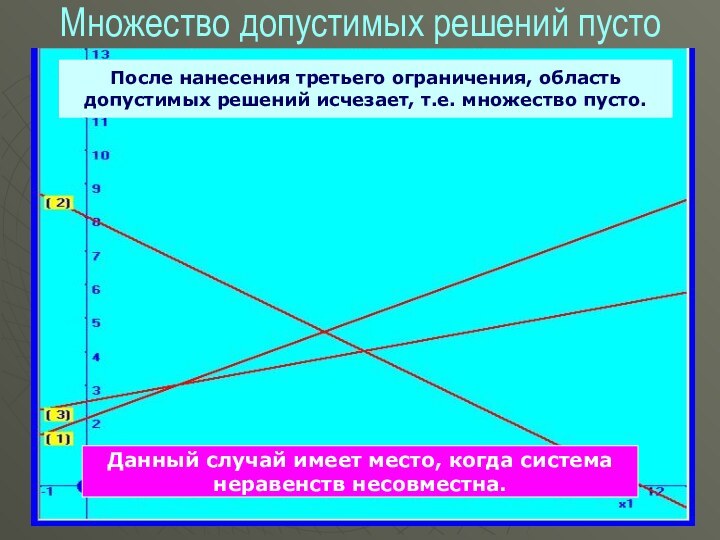
Множество допустимых решений пусто
Начинаем строить область допустимых решений.
Слайд 53
Множество допустимых решений пусто
После нанесения третьего ограничения, область
допустимых решений исчезает, т.е. множество пусто.
Данный случай имеет место,
когда система
неравенств несовместна.
Слайд 54
Экономический смысл основных и дополнительных переменных в канонической
форме задачи об оптимальном использовании ограниченных ресурсов (на примере
задачи о коврах).
7x1 +2x2 +2x3 +6x4+х5= 80,
5x1 +8x2 +4x3 +3x4+х6= 480,
2x1 +4x2 +x3 +8 x4 +х7 =130,
x1, x2, x3, x4, х5, х6, х7 ≥ 0.