Презентация на тему Полиномиальная модель

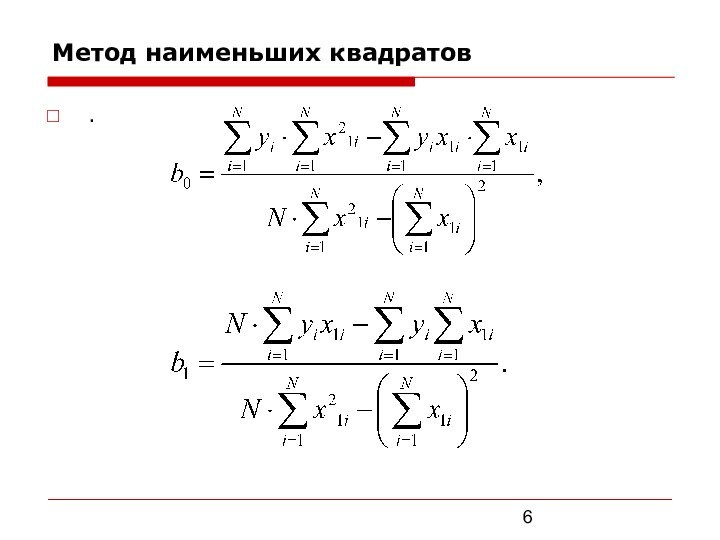
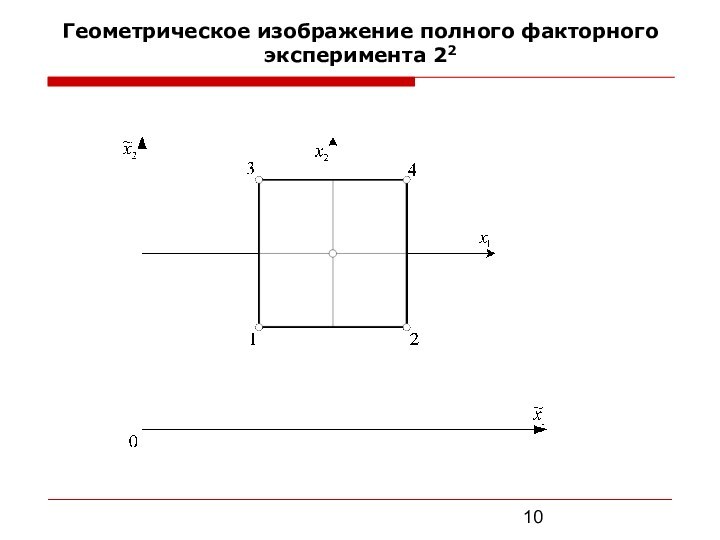
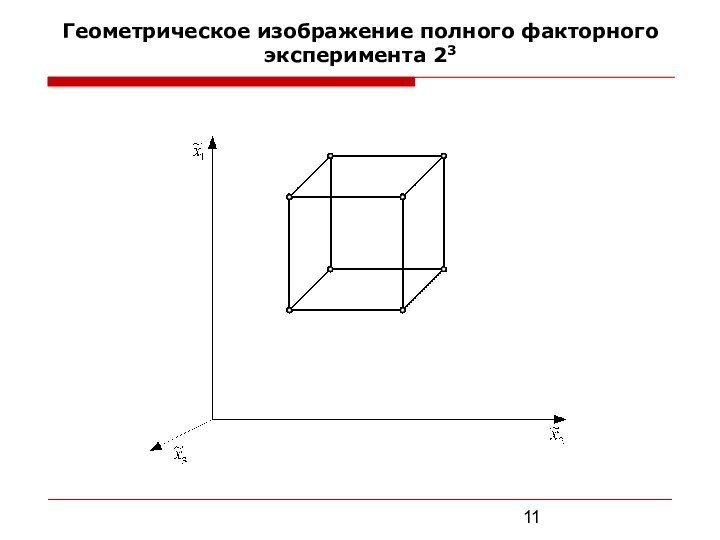
значения коэффициентов уравнения;
хi, xj - факторы;
Y - отклик;
ε -

слагаемые третьего и более высокого порядка малости.

Если модель включает в себя переменную (l - 1) степени, то данная переменная в эксперименте должна принимать не менее l значений или уровней.

соответствующих коэффициентов βi , а y - оценка отклика

Y.

N – номер опыта.



где ξi – невязка, разность между

экспериментальным и вычисленным по уравнению регрессии значениями у в i-й экспериментальной точке.

2 ..., k – номер фактора. Ноль записан для

вычисления b0.

сочетания уровней факторов, называется полным факторным экспериментом.
Если в

k – мерном пространстве фактор х1 будет прини-мать l1 уровень, фактор х2 – l2 уровней, а фактор хк – lк

уровней, то k – факторов образуют:

наборов, или точек факторного пространства.
В теории ТПЭ обычно l1 = l2 = . . . = lk поэтому N = lk. Если число уровней каждого фактора равно двум, то имеем полный факторный эксперимент типа
N = 2k.

Матрицы

планирования 23

где j – номер фактора, N – число опытов, j = 1, 2... k.
Условие нормировки


Ортогональность матрицы планирования


j ≠ u, j, u= 0, 1, 2, …, k.

каждой точке плана производят по несколько параллельных опытов (обычно

3 - 5 ).
В практике эксперимента встречаются случаи, когда отклик непроизвольно меняется под влиянием различных неконтролируемых воздействий. Они могут иметь как случайный так и периодический характер, причем период может быть меньше времени проведения эксперимента, так и значительно больше.
Для уменьшения влияния медленно изменяющихся помех используют метод, или принцип, рандомизации.