- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение циркулем и линейкой
Содержание
- 2. Цели урока:Рассмотреть новый класс задач на построение;Рассмотреть примеры задач на построение;Научиться решать такие задачи.
- 3. Оцени себя!Верные ответы тестовых заданий: b b a b a a
- 4. ОАВKLM
- 6. ЗАДАЧА 1:На данном луче от его начала
- 8. Схема решения задач на построениеАнализ (чертят рисунок
- 9. ЛИНЕЙКА ПОЗВОЛЯЕТ ПРОВЕСТИ ПРОИЗВОЛЬНУЮ ПРЯМУЮ, А ТАКЖЕ
- 10. ЗАДАЧИ НА ПОСТРОЕНИЕ:построить угол, равный данному;через данную
- 11. ПОСТРОЕНИЕ УГЛА, РАВНОГО ДАННОМУ
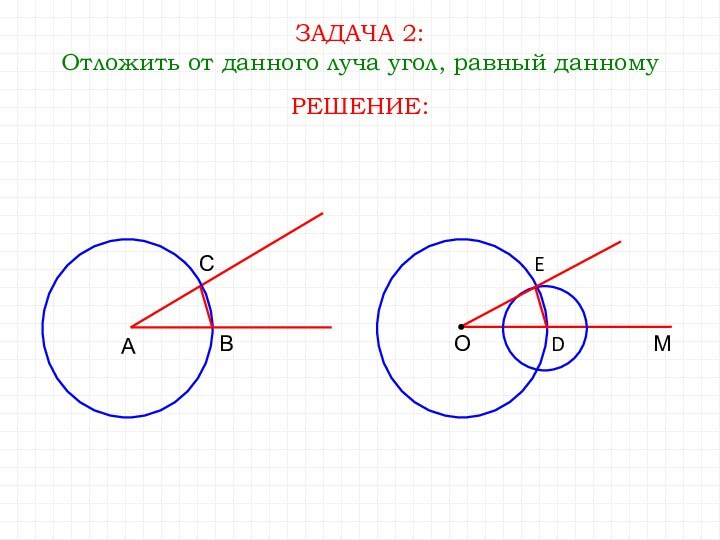
- 12. ЗАДАЧА 2:Отложить от данного луча угол, равный данномуАВОМРЕШЕНИЕ:СDE
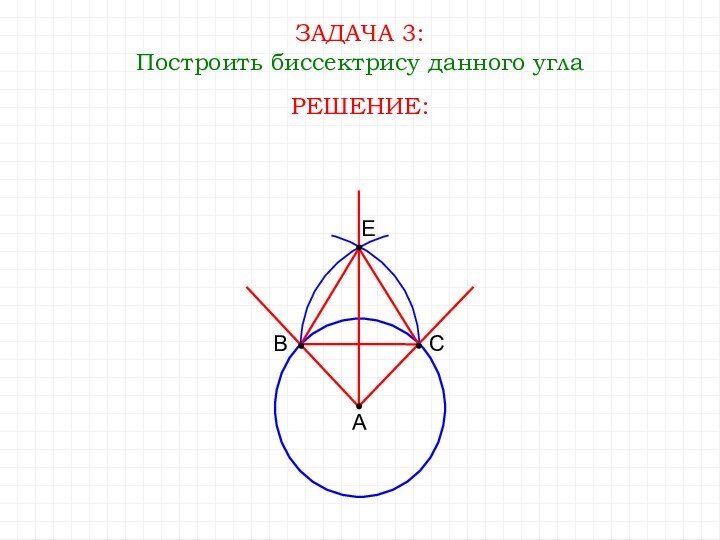
- 13. ПОСТРОЕНИЕ БИССЕКТРИСЫ УГЛА
- 14. ЗАДАЧА 3:Построить биссектрису данного углаАРЕШЕНИЕ:ВСЕ
- 15. ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРНЫХ ПРЯМЫХ
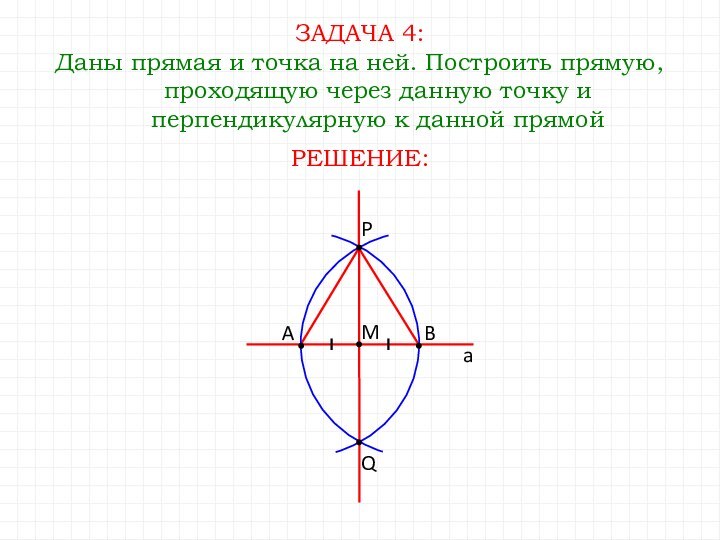
- 16. ЗАДАЧА 4:Даны прямая и точка на ней.
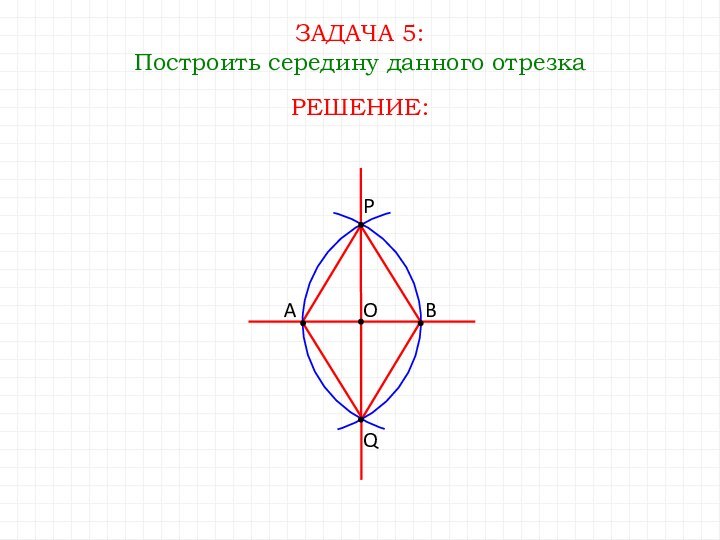
- 17. ПОСТРОЕНИЕ СЕРЕДИНЫ ОТРЕЗКА
- 18. ЗАДАЧА 5:Построить середину данного отрезкаQРЕШЕНИЕ:ABPO
- 19. Классические задачи древностиЗадача о трисекции угла. Дан
- 20. Скачать презентацию
- 21. Похожие презентации
Цели урока:Рассмотреть новый класс задач на построение;Рассмотреть примеры задач на построение;Научиться решать такие задачи.













Слайд 2
Цели урока:
Рассмотреть новый класс задач на построение;
Рассмотреть примеры
задач на построение;
Слайд 6
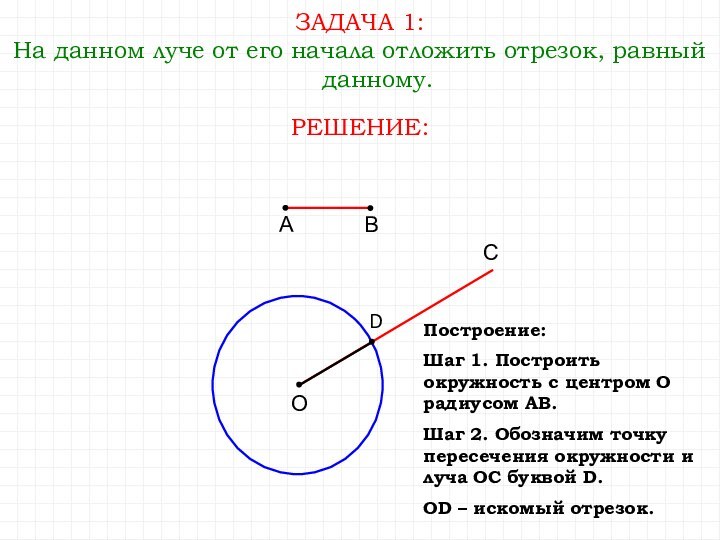
ЗАДАЧА 1:
На данном луче от его начала отложить
отрезок, равный данному.
О
С
А
В
РЕШЕНИЕ:
D
Построение:
Шаг 1. Построить окружность с центром О
радиусом АВ.Шаг 2. Обозначим точку пересечения окружности и луча ОС буквой D.
ОD – искомый отрезок.
Слайд 8
Схема решения задач на построение
Анализ (чертят рисунок искомой
фигуры, устанавливают связи между данными задачи и искомыми элементами,
а также составляют план построения).Построение по намеченному плану.
Доказательство, что данная фигура удовлетворяет условиям задачи.
Исследование( при любых ли данных задача имеет решение, и если имеет, то сколько).
В тех случаях, когда задача достаточно простая, отдельные части, например анализ или исследование, можно опустить
Слайд 9 ЛИНЕЙКА ПОЗВОЛЯЕТ ПРОВЕСТИ ПРОИЗВОЛЬНУЮ ПРЯМУЮ, А ТАКЖЕ ПОСТРОИТЬ
ПРЯМУЮ, ПРОХОДЯЩУЮ ЧЕРЕЗ ДВЕ ДАННЫЕ ТОЧКИ.
С ПОМОЩЬЮ ЦИРКУЛЯ МОЖНО
ПРОВЕСТИ ОКРУЖНОСТЬ ПРОИЗВОЛЬНОГО РАДИУСА, А ТАКЖЕ ОКРУЖНОСТЬ С ЦЕНТРОМ В ДАННОЙ ТОЧКЕ И РАДИУСОМ, РАВНЫМ ДАННОМУ ОТРЕЗКУ.
Слайд 10
ЗАДАЧИ НА ПОСТРОЕНИЕ:
построить угол, равный данному;
через данную точку
провести прямую, перпендикулярную к данной прямой;
разделить данный отрезок пополам;
и
др.
Слайд 16
ЗАДАЧА 4:
Даны прямая и точка на ней. Построить
прямую, проходящую через данную точку и перпендикулярную к данной
прямойQ
РЕШЕНИЕ:
A
B
P
M
a
Слайд 19
Классические задачи древности
Задача о трисекции угла. Дан угол
φ.Построить угол, равный трети угла φ.
Задача о квадратуре круга.
Дан круг. Построить квадрат равновеликий этому кругу.Задача об удвоении куба. Дан куб(т.е. дан отрезок, равный ребру куба), объём которого вдвое больше объёма данного куба.