- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Преобразование Фурье
Содержание
- 7. Анализ и синтез сигналов с помощью преобразования
- 8. Заполним массив s:Проводим прямое преобразование Фурье: Внимание!
- 9. Для анализа вклада отдельных гармоник в исходный сигнал изобразим на графике модули и аргументы гармоник
- 10. Проводим обратное преобразование Фурье, исключив гармоники с
- 12. Повторим преобразование Фурье, учтя слагаемые с амплитудой до 0.1.Учет дополнительных гармоник существенно улучшил результат синтеза сигналов.
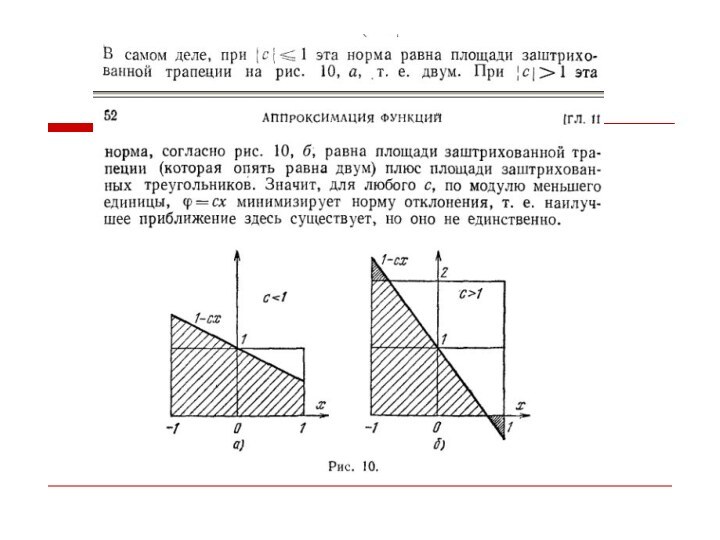
- 13. Наилучшее приближение
- 18. Скачать презентацию
- 19. Похожие презентации
Анализ и синтез сигналов с помощью преобразования Фурье. Определим функцию, задающую так называемый пилообразный сигнал и






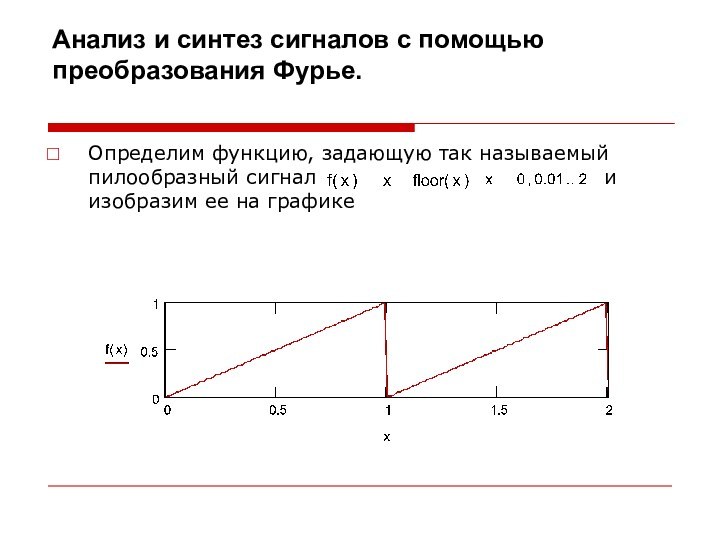










Слайд 8
Заполним массив s:
Проводим прямое преобразование Фурье:
Внимание! В
том случае, когда в массиве s содержится элементов, причем
все числа действительные, следует использовать функцию fft. Во всех остальных случаях – функцию cfft. Массив g содержит комплексные коэффициенты дискретного преобразования Фурье.Размер массива f –
Слайд 9 Для анализа вклада отдельных гармоник в исходный сигнал
изобразим на графике модули и аргументы гармоник
Слайд 10 Проводим обратное преобразование Фурье, исключив гармоники с малым
вкладом. Будем учитывать только гармоники с амплитудой не менее
0.3. Для отсечения слагаемых с малым вкладом воспользуемся функцией единичного скачка – функцией Хевисайда Ф.Для обратного преобразования Фурье используется функция ifft, если прямое преобразование осуществлялось с помощью fft, и cifft, если прямое преобразование осуществлялось с помощью cfft.