Презентация на тему к проекту Совершенные и дружественные числа, 6 класс

учащиеся 6 класса МОУ «СОШ с. Лох
Новобурасского района

Саратовской области»
Руководитель Будникова Т. А. учитель математики
2015 год

XIII районная проектно-исследовательская конференция
школьников «Я и мир вокруг»

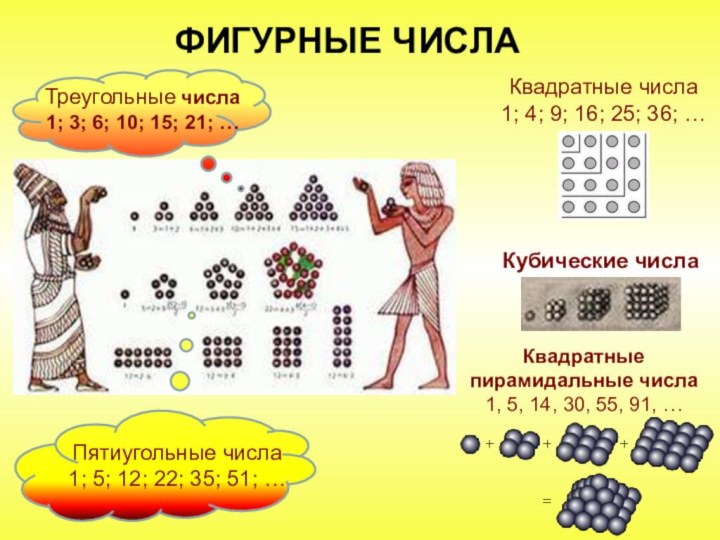
«Совершенные и дружественные числа»

Секция «Математика в моей жизни»

при выполнении информационно-исследовательского проекта.

и дружественных числах;
подобрать литературу и познакомиться с историей возникновения

совершенных и дружественных чисел;
узнать, что это за числа и какова их роль в математике;
расширить кругозор, изучая математическую литературу и материалы интернета;
составить задания по теме проекта;
вырабатывать навыки в создании и защите презентации.

математике и для математиков»

классов
Вывод: 2-е родителей, имеют представление о дружественных числах, 6

 знают, что есть совершенные числа, но никто не смог назвать ни тех, ни других.

нами.
Понять, что, как и почему,
Должны мы только

сами.

–
Источники информации –
математическая литература и Википедия
Продукт проекта –
числа

который очень много сделал для развития науки. Сначала он

занялся музыкой. Ему удалось установить связь между длиной струны музыкального инструмента и издаваемым им звуком. И тогда Пифагор решил, что не только законы музыки, но и вообще все на свете можно выразить с помощью чисел.
«Числа правят миром!» - провозгласил он.

ЧИСЛА ПРАВЯТ МИРОМ !

Первого греческого ученого, который начал
рассуждать о математике, а не только
пользоваться ею, звали Фалес.

Фалес

число можно обозначать буквой, посмотрели бы с удивлением.
И

Пифагор придумал замечательный способ доказывать общие утверждения о числах: он стал
изображать числа точками.

Натуральные числа бывают четные и нечетные.
Это знали задолго до Пифагора. Но Пифагор
стал думать о свойствах чисел.

ФИГУРНЫЕ ЧИСЛА

Доказывая свойства чисел, Пифагор
строил прямоугольники из точек.

Пифагор изображал
число 4 так: ,
а число 7 так: 

15; 21; …
Пятиугольные числа
1; 5; 12; 22; 35; 51;

…

Квадратные числа
1; 4; 9; 16; 25; 36; …

Квадратные пирамидальные числа
1, 5, 14, 30, 55, 91, …

Кубические числа

4  оно является первым произведением двух равных множителей:

4 = 22 .

СОВЕРШЕННЫЕ ЧИСЛА

Но фигурными числами Пифагор не удовлетворился.
Ведь он провозгласил, что числа правят миром.
Поэтому ему пришлось придумывать, как с
помощью чисел изображать такие понятия, как
справедливость, совершенство, дружба.

Чтобы изобразить совершенство, Пифагор принялся

за делители чисел. Делитель числа назвали
правильным, если он меньше самого числа.

Все правильные делители числа Пифагор складывал.
Если сумма делителей оказывалась меньше числа, то число
объявлялось недостаточным, а если больше  избыточным.
А если сумма делителей в точности равнялась числу, то число
объявляли совершенным.

делители числа 496:
1; 2; 4; 8; 16; 31,

62, 124, 248.
Сумма правильных делителей
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496.
Значит, число 496  совершенное число.

Во времена Пифагора было известно три совершенных числа: 6; 28; 496 !

Пифагореец Ямвлих: «Всё совершенное редко встречается
в мире. Редко встречаются и совершенные числа».

Ямвлих
VI век до н.э.

Евклид
III век до н.э.

Евклид указал формулу для вычисления четных совершенных чисел: 2p - 1  (2p - 1).

Леонард Эйлер
(1707  1783 гг.)

Русский математик
Л. Эйлер доказал утверждение,
указанное Евклидом.

9  2658455991569831744654692615953842176,
№ 10  191561942608236107294793378084303638130997321548169216, …

числами дружбу  два числа называли дружественными,

если каждое из них равнялось сумме делителей другого
числа. Найти пример дружественных чисел потруднее.

Проверим, что «дружат» числа 220 и 284.
Делители 220: 1; 2; 4; 5; 10; 11; 20; 22; 44; 55; 110; 220.
Сумма правильных делителей числа 220:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284.
Делители числа 284: 1; 2; 4; 71; 142; 284.
Сумма правильных делителей числа 284.
1 + 2 + 4 + 71 + 142 = 220.
Вывод: Да, 220 и 284 дружественные числа.

Дружественные числа

И

которые, знали только одну пару таких чисел —
220 и

284.
 

Много столетий спустя
Л. Эйлер нашёл ещё 65 пар дружественных чисел.
Одна из них — 17296 и 18416.  

Арабский астроном и математик Сабит ибн Курра (826—901) ввел формулу, по которой нашел две новые пары дружественных чисел.

На сентябрь 2007 года известно 11.994.387 пар дружественных чисел. Все они состоят из чисел одной чётности.

Использование ЭВМ позволило отыскать несколько сотен пар дружественных чисел. Известны два двадцатипятизначных дружественных числа.

 

дружественных чисел. Б. Квадрат десятого простого числа. В. Третье

совершенное число.
По вертикали: А. Другое число из первой пары дружественных чисел.
Г. Квадрат четвертого простого числа. Д. Однозначное совершенное число.

Составленные нами задания

Кросснамбер 3  3.
Наш конструктор числовой, поработай головой!

1. Число, равное сумме своих правильных

делителей.
2. Автор тринадцати книг «Начала» по математике.
3. Числа, каждое из которых равняется сумме
правильных делителей другого числа.
4. Наименьшее из всех натуральных чисел.
5. Раздел математики с буквенной символикой.
6. Точное предписание о выполнении в
определенном порядке системы действий.
7. Международная стандартная единица
измерения длины.
8. Отрезок, соединяющий точку окружности
с ее центром.

важны»


По вертикали:
1) Натуральное числа, имеющие более

двух делителей. 2) Число, составленное Пифагором из точек. 3) Число, имеющие только два делителя. 4) Число, имеющие числитель и знаменатель. 5) Натуральные числа, им противоположные и число нуль называются…
По горизонтали:
6) Два числа, равны сумме правильных делителей другого числа.

двух делителей.
2) Целое число, которое не делится на

2.
3) Натуральное число, имеющее только два делителя. 4) Число, состоящее из целой и дробной части.
По горизонтали:
5): Число, равное сумме своих правильных делителей.

Кроссворд
«Какие бывают числа»

Но нельзя забывать, что с этих забав началось

серьёзное
знакомство людей с числами. Числа стали не только
применять, но и изучать. Так возник раздел математики
«Теория чисел».

Многие проблемы теории чисел может понять любой
шестиклассник. Но решение этих проблем настолько сложно,
что на них ушли столетия.
До сих пор не известен общий способ нахождения пар дружественных чисел.
До сих пор неизвестно ни одного нечётного совершенного числа, но и не доказано, что их не существует.

Совершенные и дружественные числа не имеют широкого
применения, поэтому и не изучаются на уроках математики.

учебника
математики, историей развития математической

науки нужно знакомить учащихся. Чтобы ученики:
любили математику! интересовались математикой!
уважали математику!

Перспектива проекта

Использование презентации и заданий на занятиях
математического кружка и элективных курсов для
расширения кругозора учащихся.