Презентация на тему Метод мажорант

на едином государственном экзамене, есть задачи, требующие специальных методов

решения, которые, к сожалению, не изучаются в школе. Один из таких методов-метод мажорант. Красивейший способ решения сложных задач.

задач методом мажорант

называется такое число M, что либо f(x) ≤M для

всех x є P, либо f(x) ≥ M для всех x є P.

.

f(x)=sin

x
-1≤ sin x ≤ 1
M=1, M=-1


f(x)=cos x
-1≤ cos x ≤ 1
M=1, M=-1

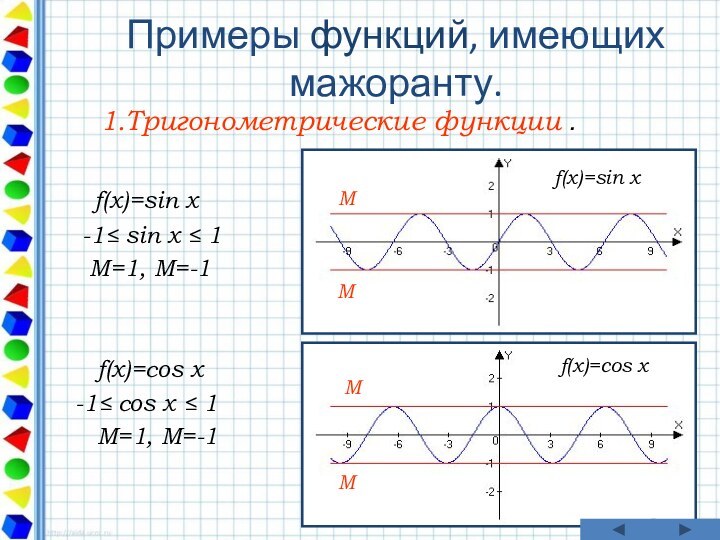
f(x)=sin x

f(x)=cos x

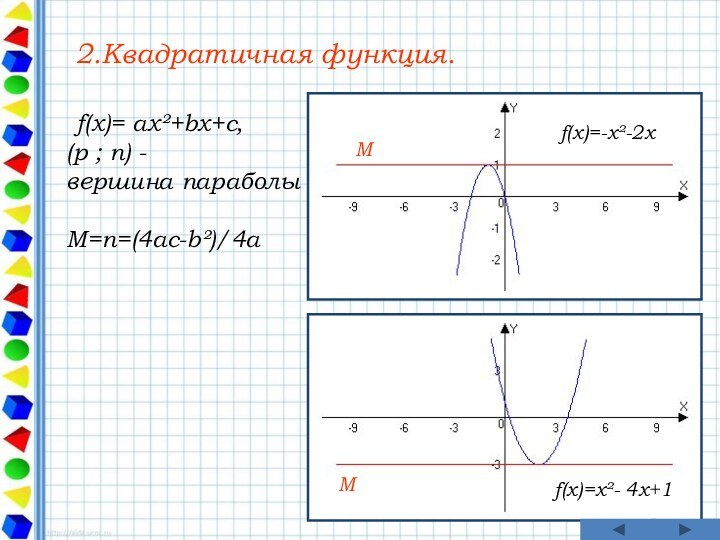
M

M

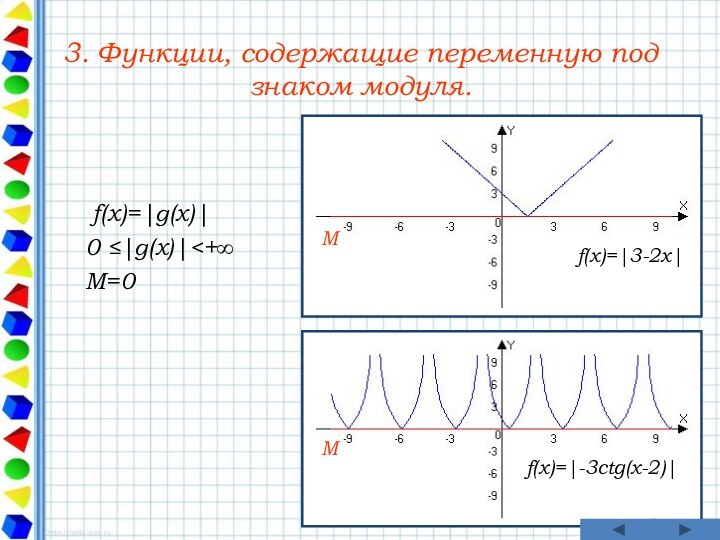
M

M

-
вершина параболы

M=n=(4ac-b²)/4a





f(x)=-x²-2x
M
M
f(x)=x²- 4x+1

f(x)=|g(x)|
0 ≤|g(x)|

f(x)= √g(x)
0 ≤

√g(x) <+∞

M=0

M

M

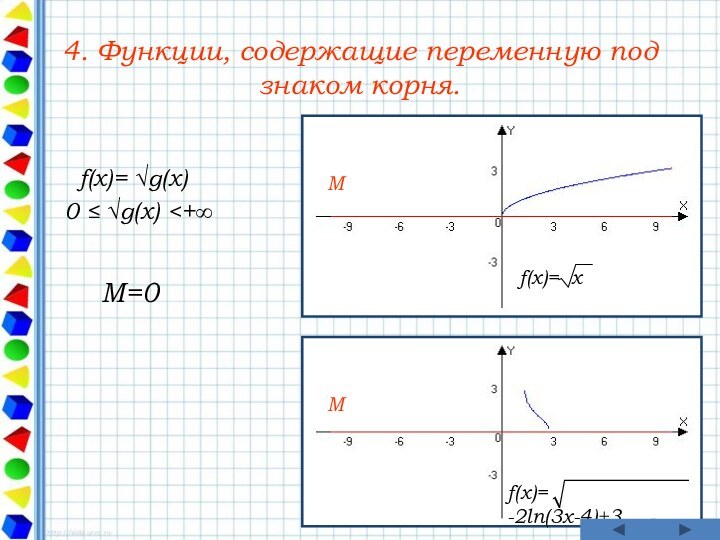
f(x)= x

f(x)= -2ln(3x-4)+3

для того, чтобы определить мажоранту, нужно провести исследование функции,

применяя различные методы . При этом можно использовать свойства неравенств, некоторые известные равенства и неравенства, определение возрастающей и убывающей
функций и т. д.

– некоторые функции, определённые на множестве D. Пусть f(x)

ограничена на этом множестве числом А сверху, а g(x) ограничена на этом множестве тем же числом А, но снизу. Тогда уравнение f(x) = g(x) равносильно системе уравнений

Теорема 2. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) и g(x) ограничены на этом множестве снизу (сверху) числами А и В соответственно. Тогда уравнение f(x) + g(x) = A+B равносильно системе уравнений

Теорема 3. Пусть f(x) и g(x) – некоторые неотрицательные функции, определённые на множестве D. Пусть f(x) ограничена сверху ( или снизу) числами А и В соответственно. Тогда уравнение f(x)·g(x)= А·B равносильно системе уравнений (при условии, что A>0 и B>0)

1.Найдите мажоранту и

область значения функции (Рассмотрим два способа.)

1. Графический.











Очевидно, E (f) =[3;+∞], М=0

M

2. Аналитический.
Оценим выражение

0 ≤ x² <+∞
1≤ x²+1<+∞
3≤ <+∞
E (f) =[3;+∞], М=0
Очевидно, что графический
способ не всегда удобен, так
как может потребоваться
строить графики очень
сложных функций! Поэтому
мы будем учиться решать
такие задания аналитически!

f(x)=

Решение.

0 ≤ 3sin²x ≤ 3
1 ≤ 1 + 3sin ² x ≤ 4

0 ≤ log (1+3sin x) ≤ 2


0,25 ≤ 0,5 ≤ 1

E(f) = [ 0,25; 1]

Задания для самостоятельной работы.

f(x)=

2

2

log (1+3sin x)

0,5

log (1+3sin x)

2

2

2

2

1) f(x) =

1

1-2

4

x

2) f(x) =

3

7

log

17+ 16+ lg x

3) f(x) =

8

π

( (3sinx-cosx+2))

arctg

1

4

работы.

 

Пример.

Решение.

-x

2

2

1

1

3

3

2

log (4-|x|) ≤ 2.

3 + 3 = 2

log (4-|x|) = 2

≥ 2 , то

x

а) Так как

б) 4-|x|≤ 4

a +

x

Из а), б) получим

a

+

x

≥ 2.

Ю

-x

⇔

x = 0

1) 2 sinxcosx = sin46º

2) сos²(sinx)=1+ log (x²-6x+10)

3) 2 + 2 = -4x² - x²

1

4)

x+1

x²- 4x +5

1-x

1

10

1

+

x²- 4x +29

1,4

=

Пример.




Решение.

Правая часть неравенства
не больше 1, левая –
больше 1, значит, корней
нет.

Задания для самостоятельной работы.

cosx - z³ ≥ y² +

3

π

а) 1≤ cosx ≤ 1

- ∞< cosx - z ³ ≤ 1

+

- ∞< - z ³ ≤ 0

б) y² + ≥ >1

3

π

π

3

1) 2 - 2cosx + y - x²-1 ≤0

y

2) 2x + 2- x ² ≥ 3

x ² -2x+2

2

3) x² + 4x + 6≤

y ² - 6y +10

6

4) cos3x ≤ x +1

котором
решение неравенства
||2x+4|-7|-13 ≤ 2c ²
удовлетворяет условию
x є

[-37;35].
Решение.
-37 ≤ x ≤ 35
-70 ≤ 2x+4 ≤ 74
0 ≤│2x+4│≤ 74
0 ≤ ││2x+4│-7│≤ 67
-13 ≤ ││2x+4│-7│-13 ≤ 54
Для выполнения неравенства,
надо, чтобы -13≤2с²≤54.
То есть наибольшее целое
с=5.

Задания для самостоятельной работы.
1) Найти сумму целых значений
функции


2) Из множества значений функции



удалили целые числа. Сколько
получилось числовых
промежутков?

2

f(x)=3 36cos x -12sinx + 27

2

sin2x + cos2x

f(x)= 3+ 4arcsin

Решите неравенство
Решение.

Так как, левая часть неравенства не больше1, а правая -

равна 1, то

7 · log (6x-x ² -7) ≥ 1

2

-|x- 3|

a) 0 < 7 ≤ 1

-|x-3|

б) log (6x-x ²-7)=log (2-(x-3) ²) ≤ log 2 =1

2

2

2

log (6x-x ² -7) =1

2

7 = 1

-|x- 3|

⇔

x = 3