Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Применение инверсии в построении графиков элементарных функций

Содержание

Цели урока: • Повторить способы построения графиков известными методами преобразований. • Познакомить учащихся с наиболее эффективным методом построения графика функции вида и
Поташникова Елена Михайловна Косовцева Наталья Ивановна Химки, 2011 Цели урока: • Повторить способы построения графиков известными yx-111-10f(x) Графики данных функций: нельзя построить с помощью рассмотренных преобразований. Точка В называется инвертной точке А относительно прямой (оси) 0yx1yx101Относительно ОХ:(x,y) -> (x, )Относительно ОУ:(x,y) -> ( , у) xy1-11Г → ГГ2+x2 → Г2+( )2-112ухОтносительно ОХ:Относительно ОУ:Инверсия
Слайды презентации

Слайд 2 Цели урока: • Повторить способы построения

Цели урока: • Повторить способы построения графиков известными методами

графиков известными методами преобразований. • Познакомить учащихся с

наиболее эффективным методом построения графика функции вида и .

Слайд 3

Слайд 4 y
x
-1
1
1
-1
0
f(x)

yx-111-10f(x)

Слайд 5 Графики данных функций:
нельзя построить с помощью рассмотренных

Графики данных функций: нельзя построить с помощью рассмотренных преобразований.

преобразований.

Слайд 6 Точка В называется инвертной точке А относительно

Точка В называется инвертной точке А относительно прямой (оси)

прямой (оси) e, если: • Эти точки лежат по

одну сторону относительно прямой (оси) e. • АВ ┴ e • ОА∙ОВ = 1

Инверсия

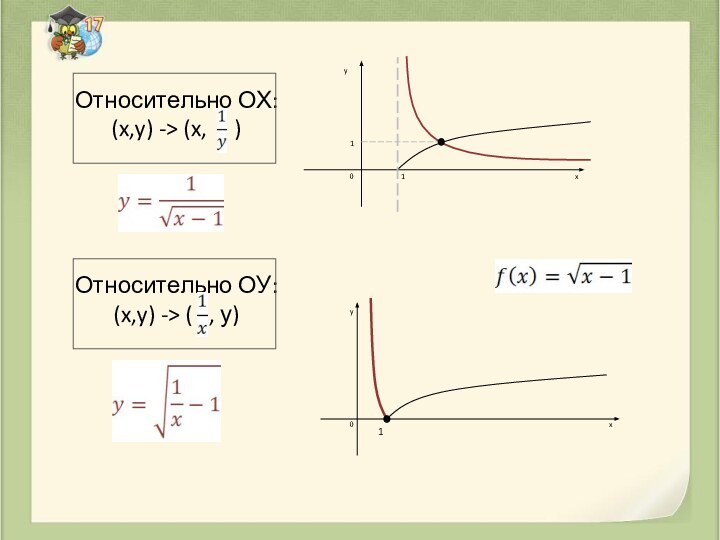
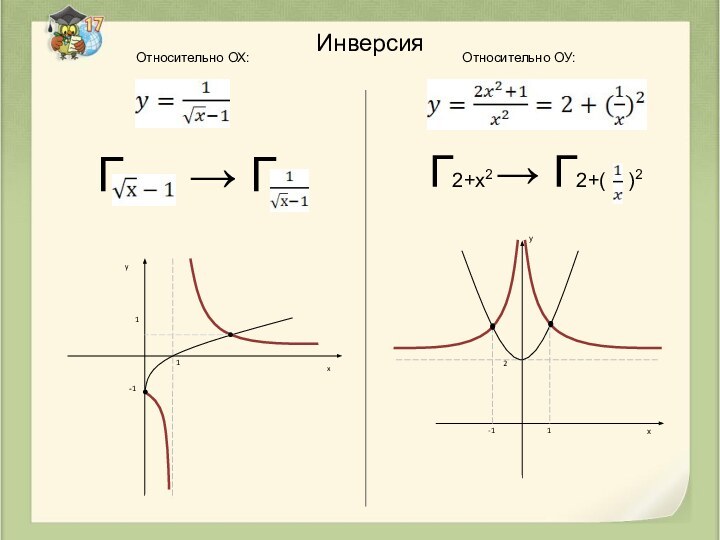
Относительно ОХ:
(x,y) -> (x, )


Относительно ОУ:
(x,y) -> ( , у)


Если у = ±1 , то точка переходит сама в себя

Если у = 0, то → ∞

Если х = ±1 , то точка переходит сама в себя

Если х = 0, то → ∞

Слайд 7 0
y
x
1
y
x
1
0
1
Относительно ОХ:
(x,y) -> (x, )


Относительно ОУ:
(x,y)

0yx1yx101Относительно ОХ:(x,y) -> (x, )Относительно ОУ:(x,y) -> ( , у)

-> ( , у)


  • Имя файла: primenenie-inversii-v-postroenii-grafikov-elementarnyh-funktsiy.pptx
  • Количество просмотров: 101
  • Количество скачиваний: 0
- Предыдущая Из истории обыкновенных дробей (5 класс)
Следующая - Кот Снупи

Похожие презентации

Графики квадратичных функций Графики квадратичных функций 111
Эталоны-помощники учителей и учеников. методическая разработка по математике Эталоны-помощники учителей и учеников. методическая разработка по математике 100
Математическое шоу Математическое шоу 168
Математические кроссворды Математические кроссворды 126
Презентация к выступлению Потенциал текстовых задач для формирования УУД Презентация к выступлению Потенциал текстовых задач для формирования УУД 112
Ломаная геометрия Ломаная геометрия 182
Вводный урок Вводный урок 137
Деление столбиком 4 класс план-конспект урока по математике (4 класс) Деление столбиком 4 класс план-конспект урока по математике (4 класс) 132
Как измеряли в старину Как измеряли в старину 117
Презентация по математике на тему Окружность (5 класс) Презентация по математике на тему Окружность (5 класс) 134
Проект Академия РостА презентация к уроку по математике (подготовительная группа) Проект Академия РостА презентация к уроку по математике (подготовительная группа) 132
Презентация Комбинированные задачи в стихах от фей Презентация Комбинированные задачи в стихах от фей 120
Презентация по математике на тему Оригами. Первое занятие Презентация по математике на тему Оригами. Первое занятие 101
Сложение и вычитание многочленов Сложение и вычитание многочленов 159
Парабола Парабола 126
Неделя Математики (работа учеников) Неделя Математики (работа учеников) 122
Единицы измерения времени Единицы измерения времени 126
Конспект урока по математике Вычитание вида 54-26 план-конспект урока по математике (2 класс) Конспект урока по математике Вычитание вида 54-26 план-конспект урока по математике (2 класс) 139
тест Табличное сложение и вычитание в пределах 20 тест по математике (1 класс) по теме тест Табличное сложение и вычитание в пределах 20 тест по математике (1 класс) по теме 118
Технологическая карта урока математики.Тема: Письменное деление на число оканчивающиеся нулями. УМК Школа России. план-конспект урока по математике (4 класс) Технологическая карта урока математики.Тема: Письменное деление на число оканчивающиеся нулями. УМК Школа России. план-конспект урока по математике (4 класс) 162
Умножение и деление десятичной дроби на 10, 100, 1000 и т.д. Умножение и деление десятичной дроби на 10, 100, 1000 и т.д. 110
Тренажёр по математике презентация к уроку по математике (1 класс) по теме Тренажёр по математике презентация к уроку по математике (1 класс) по теме 112
Выделение в числе общего количества единиц любого разряда Выделение в числе общего количества единиц любого разряда 317
Раздел Сложение Раздел Сложение 123
Число и цифра 3. презентация урока для интерактивной доски по математике (1 класс) Число и цифра 3. презентация урока для интерактивной доски по математике (1 класс) 145
Математика Аралас сандарды көбейту Математика Аралас сандарды көбейту 114
Дидактическая игра Четвертый лишний презентация по математике Дидактическая игра Четвертый лишний презентация по математике 156
Круг Луллия. Цвет и форма методическая разработка по математике (средняя группа) Круг Луллия. Цвет и форма методическая разработка по математике (средняя группа) 52
Обобщение опыта по теме Развитие познавательных и математических способностей детей Нечаева Ирина Владимировна презентация по математике Обобщение опыта по теме Развитие познавательных и математических способностей детей Нечаева Ирина Владимировна презентация по математике 115
Игра Умники и умницы Игра Умники и умницы 115