Слайд 2
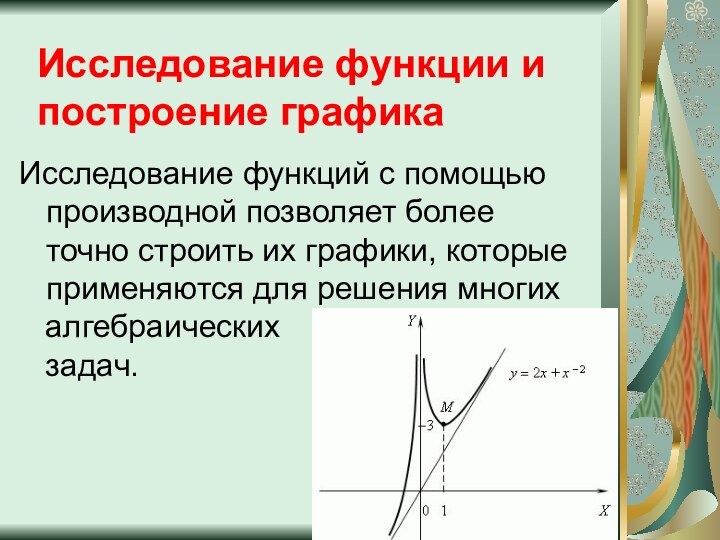
Исследование функций с помощью производной позволяет более точно
строить их графики, которые применяются для решения многих
алгебраических
задач.
Исследование функции и построение графика
Слайд 3
Схема исследования функции
Область определения
Чётность, нечётность
Периодичность
Точки пересечения графика с
осями координат
Промежутки знакопостоянства
Монотонность
Точки экстремума и значения f в этих
точках
Наибольшее и наименьшее значение f
Вспомогательные точки
График функции(точный или эскиз)
Слайд 4
Область определения функции
Множество всех значений аргумента, при котором
функция определена.
D(f)
Слайд 5
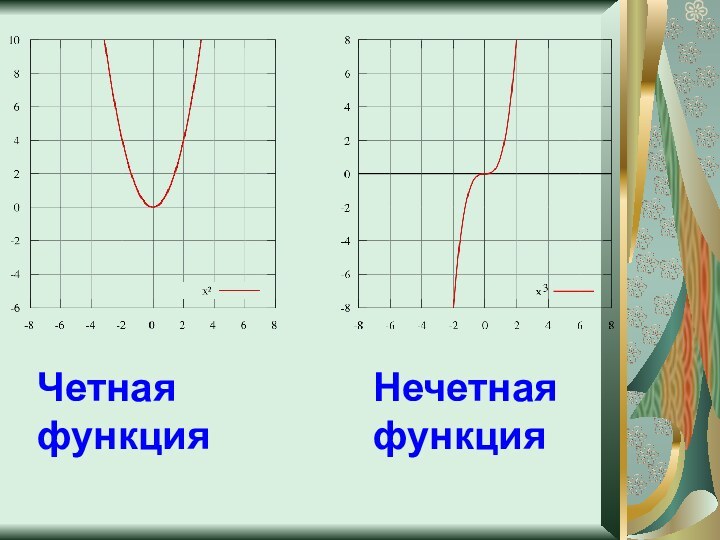
Чётность, нечётность
D(f)-симметрична относительно О(0;0).
Если f(-x)=f(x)-функция четная.
Если f(-x)=-f(x)-функция нечетная.
Если
функция ни та, и ни другая, то она общего
вида!
Слайд 6
Четная функция
Нечетная функция
Слайд 7
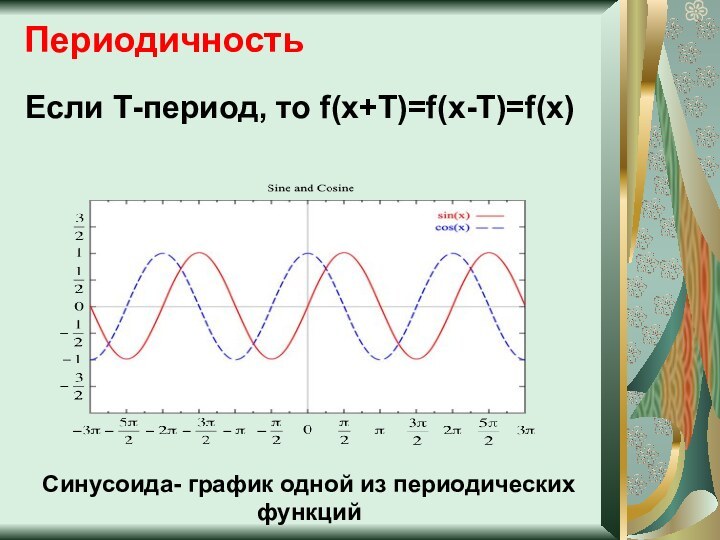
Периодичность
Если Т-период, то f(x+T)=f(x-T)=f(x)
Синусоида- график одной из периодических
функций
Слайд 8
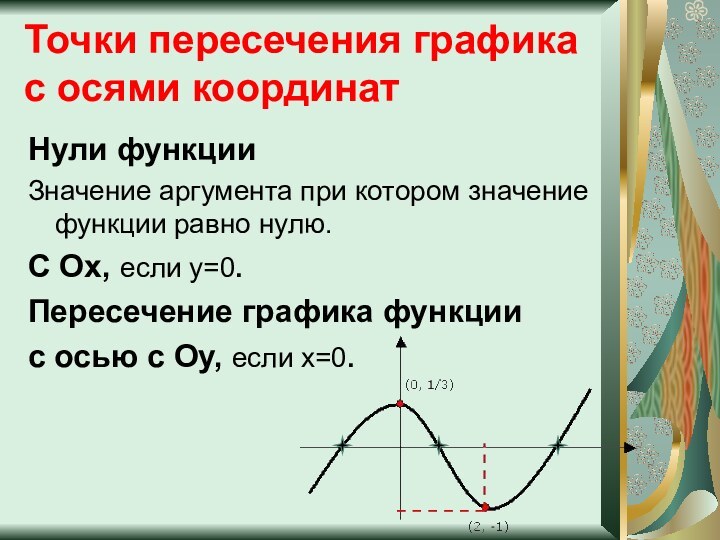
Точки пересечения графика с осями координат
Нули функции
Значение аргумента
при котором значение функции равно нулю.
С Ох, если
y=0.
Пересечение графика функции
с осью с Оу, если х=0.
Слайд 9
Промежутки знакопостоянства
Промежутки знакопостоянства – интервалы, на которых функция
положительна или отрицательна, или, иначе, решения неравенств f(x) >
0 и f(x) < 0.
y>0, при х ε [a;b];
y<0, при х ε [a1;b1].
Слайд 10
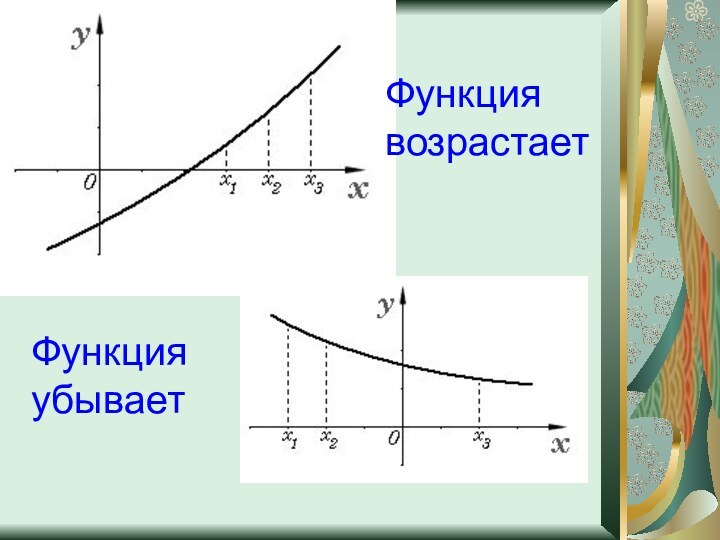
Монотонность
Функция f (x) называется возрастающей на промежутке D,
если для любых чисел x1 и x2 из промежутка
D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).
Или выполняется условие f ‘(x)>0
Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 > x2, выполняется неравенство f (x1) > f (x2).
Или выполняется условие f ‘(x)<0
Промежутки возрастания и убывания – интервалы, на которых функция или возрастает, или убывает. Слова “возрастание” и “убывание” функции иногда заменяют одним словом – “монотонность” функции.
Слайд 11
Функция возрастает
Функция убывает
Слайд 12
Экстремумы
Точки экстремума – точки, лежащие внутри области определения,
в которых функция принимает самое большое (максимум) или самое
малое (минимум) значение по сравнению со значениями в близких точках
Если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума
Если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка минимума.
Слайд 13
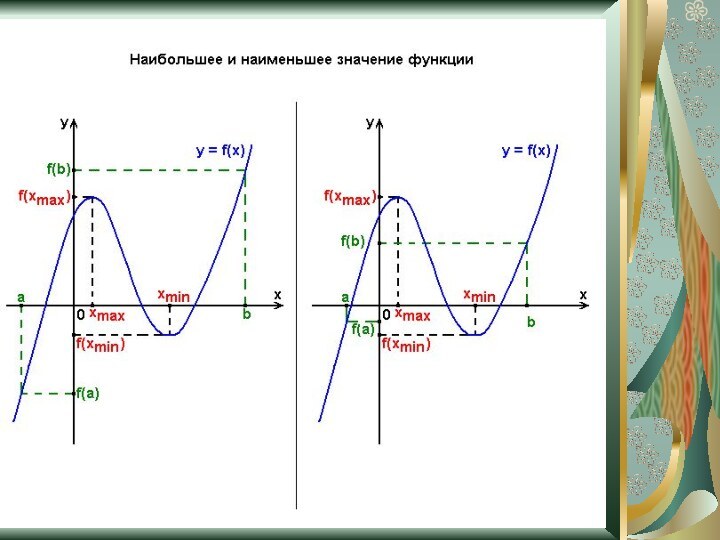
Множество значений функции
Наибольшее и наименьшее значение
Множество значений функции
– множество чисел, состоящее из всех значений функции.
E(f)
Непрерывная
на отрезке [a;b] функция f принимает на этом отрезке наибольшее и наименьшее значение, либо на концах промежутка, либо в критических точках, в которых f‘=0
Слайд 15
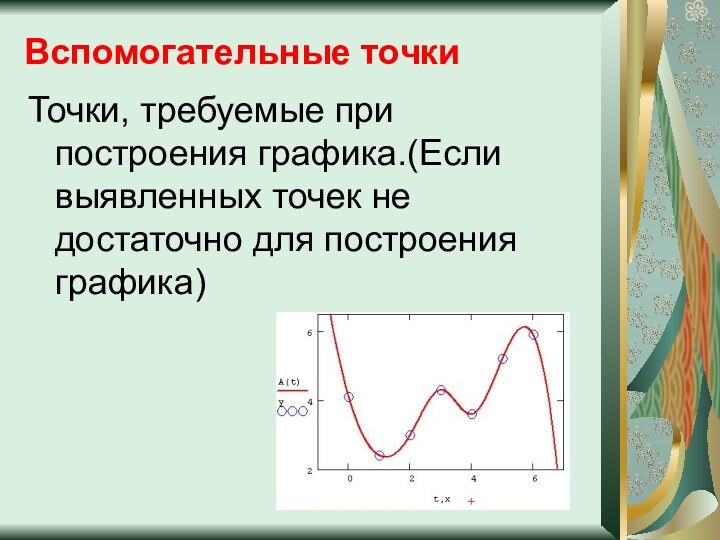
Вспомогательные точки
Точки, требуемые при построения графика.(Если выявленных точек
не достаточно для построения графика)
Слайд 16
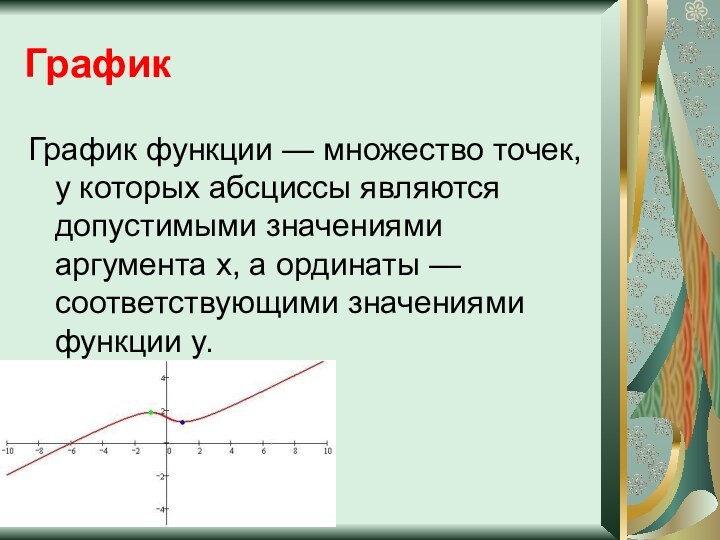
График
График функции — множество точек, у которых абсциссы
являются допустимыми значениями аргумента x, а ординаты — соответствующими
значениями функции y.
Слайд 18
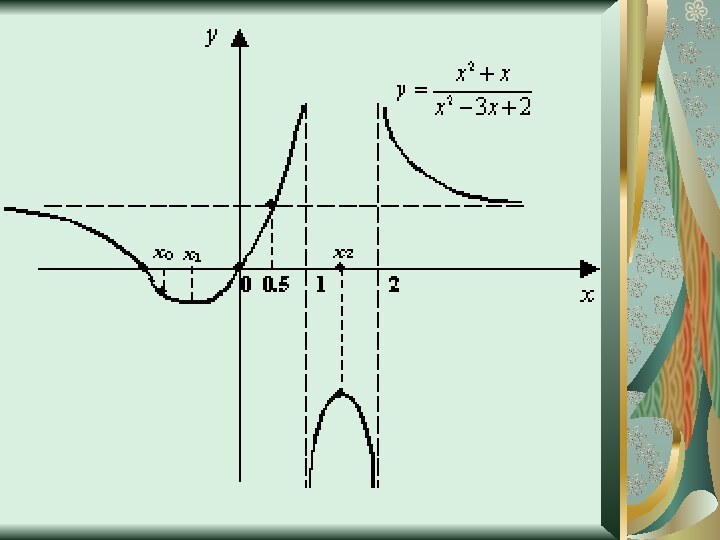
Исследование функции
y=(x2+x)/(x2-3x+2)
Упростим выражение
y=(x2+x)/(x2-3x+2); y=(x2+x)/((x-1)*(x-2))
D(f)=R\1,2
Функция общего вида,
т.к.f(-x)≠f(x) и f(-x)≠ -f(x)
Непериодическая
С осью оy x=0, тогда y=0; C осью ox y=0, тогда (x2+x)/(x2-3x+2)=0 x2+x=0 x*(x+1)=0 x=0 или x=-1
Слайд 19
Промежутки знакопостоянства
Находим производную функции
y’=(-4x2+4x+2)/((x-1)2*(x-2)2)
D(f’)=R\1;2
Находим промежутки возрастания и убывания функции
(-4x2+4x+2)/((x-1)2*(x-2)2)=0
-4x2+4x+2=0
x1=
(-1+√3)/-2≈1,4;
x2= (-1-√3)/-2≈-0,4;
Слайд 20
Экстремумы
x= (-1+√3)/-2 -точка минимума;
y((-1+√3)/-2)=(2-2√3)/(3+2√3)
x= (-1-√3)/-2-точка максимума;
y((-1+-√3)/-2)=(2+2√3)/(3-2√3)
9.
E(y)=(-∞;(2-2√3)/(3+2√3)U(2+2√3)/(3-2√3);+∞)
10. График