Слайд 2
Сведения из истории появления производной:
Лозунгом многих математиков XVII
в. был: «Двигайтесь вперёд, и вера в правильность результатов
к вам придёт».
• Термин «производная» - ( франц. deriveе - позади, за) ввёл в 1797 г. Ж . Лагранж. Он же ввёл современные обозначения y ' , f ‘.
обозначение lim –сокращение латинского слова limes (межа, граница). Термин «предел» ввёл И. Ньютон.
• И. Ньютон называл производную флюксией, а саму функцию - флюентой.
Г. Лейбниц говорил о дифференциальном отношении и обозначал производную так:
Лагранж Жозеф Луи (1736-1813)
французский математик и механик
Слайд 3
Ньютон:
« Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон.» А.Поуг.
Исаак
Ньютон (1643-1727) один из создателей дифференциального исчисления.
Главный его труд- «Математические начала натуральной философии»-оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.
Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Слайд 4
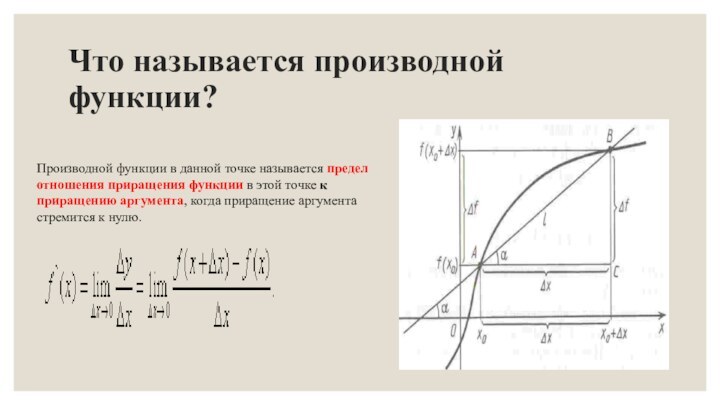
Что называется производной функции?
Производной функции в данной точке
называется предел отношения приращения функции в этой точке к
приращению аргумента, когда приращение аргумента стремится к нулю.
Слайд 5
Физический смысл производной.
Скорость есть производная от пути
по времени:
v(t) = S′(t)
Ускорение есть производная скорости по времени:
a(t) = v′(t) = S′′(t)
Слайд 6
Геометрический смысл производной:
•Угловой коэффициент касательной к графику функции
равен производной этой функции, вычисленной в точке касания.
f′(x) = k = tga
Слайд 7
Производная в электротехнике:
В наших домах, на транспорте, на
заводах : всюду работает электрический ток. Под электрическим током
понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.
В электротехнике в основном используется работа переменного тока.
Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.
Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.
Слайд 8
Производная в химии:
И в химии нашло широкое применение
дифференциальное исчисление для построения математических моделей химических реакций и
последующего описания их свойств.
Химия – это наука о веществах, о химических превращениях веществ.
Химия изучает закономерности протекания различных реакций.
Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.
Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.
Слайд 9
Производная в географии:
Идея социологической модели Томаса Мальтуса состоит
в том, что прирост населения пропорционально числу населения в
данный момент времени t через N(t), . Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.
Слайд 11
Немного из истории:
История понятия интеграла уходит корнями к
математикам Древней Греции и Древнего Рима .
Известны работы
учёного Древней Греции - Евдокса Книдского (ок.408—ок.355 до н.э.) на нахождение объёмов тел и вычисления площадей плоских фигур.
Слайд 12
Большое распространение интегральное исчисление получило в XVII веке.
Учёные: Г. Лейбниц (1646-1716) и И
. Ньютон (1643-1727) открыли независимо друг от друга и практически одновременно формулу, названную в последствии формулой Ньютона - Лейбница, которой мы пользуемся. То, что математическую формулу вывели философ и физик никого не удивляет, ведь математика—язык, на котором говорит сама природа.
Слайд 13
Символ введен
Лейбницем (1675 г.). Этот знак является
изменением латинской буквы S
(первой буквы слова сумма). Само
слово интеграл придумал
Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integero, которое переводится как приводить в прежнее состояние, восстанавливать.
Пределы интегрирования указал уже Л.Эйлер (1707-1783). В 1697 году появилось название новой ветви математики - интегральное исчисление. Его ввёл Бернулли.
Слайд 14
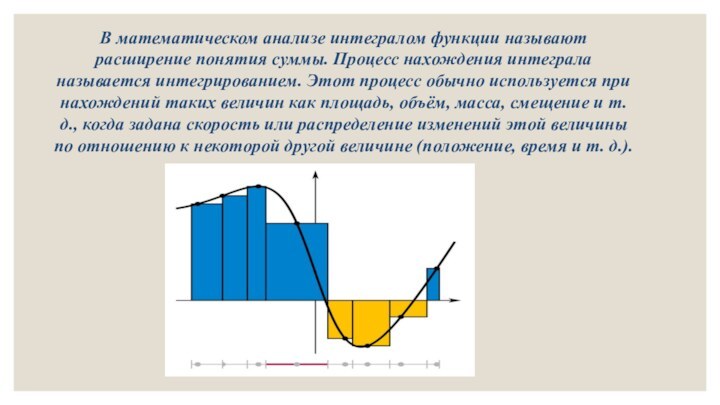
В математическом анализе интегралом функции называют расширение понятия
суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно
используется при нахождений таких величин как площадь, объём, масса, смещение и т. д., когда задана скорость или распределение изменений этой величины по отношению к некоторой другой величине (положение, время и т. д.).
Слайд 15
Что такое интеграл?
Интеграл — одно из важнейших понятий математического анализа,
которое возникает при решении задач о нахождении площади под
кривой, пройденного пути при неравномерном движении, массы неоднородного тела, и т. п., а также в задаче о восстановлении функции по её производной
Слайд 16
Ученые стараются все физические явления выразить в виде
математической формулы. Как только у нас есть формула, дальше
уже можно при помощи нее посчитать что угодно. А интеграл — это один из основных инструментов работы с функциями.
Слайд 17
Методы интегрирования:
Табличный.
Сведение к табличному преобразованием подынтегрального выражения в
сумму или разность.
Интегрирование с помощью замены переменной (подстановкой).
Интегрирование по
частям.