Слайд 2
СОДЕРЖАНИЕ ТЕМЫ
Введение
Виды неравенств
Свойства числовых
неравенств
Действия с двойными
неравенствами
Доказательства
неравенств
Решение
линейных
неравенств
Система линейных
неравенств
Решение системы
линейных неравенств
Дидактический
материал по теме
Контрольные вопросы
по теме
Слайд 3
При сравнении двух действительных
чисел Х и У возможны
три случая:
Х=У (если Х
– У = 0)
Х>У (если Х – У > 0)
Х<У (если Х – У < 0)
Запись Х≥У (Х≤У) означает, что либо
Х>У, либо Х=У и читается так:
«Х больше или равно У» или
«Х не меньше У»
Запись, в которой два числа или два выражения, содержащие
переменные, соединены знаком >,<,≥ или≤ называется
неравенством.
Слайд 4
Неравенства могут быть :
Строгими (неравенство
составлено с помощью
знаков > или
)
Нестрогими (неравенство
составлено с помощью
знаков ≤ или ≥ )
Двойными (вместо двух
неравенств х<а, а<у
употребляется запись
х
Слайд 5
Числовыми (неравенство содержит только числа)
Верными (если неравенство представляет
собой истинное высказывание: 2
неравенство представляет собой ложное высказывание: -4>15)
Равносильными (если
множества решений этих
неравенств совпадают)
Слайд 6
Рассмотрим свойства числовых неравенств :
1. для любых чисел
a и b: если a>b, то b
чисел a,b и c таких, что a>b, a b>c, верно: a>c (свойство транзитивности)
3. если a>b и c-любое число, то a+c=b+c
4. если a>b и c>0, то ac>bc
5. если a>b и c<0, то ac6. если a>b>0, то
Слайд 7
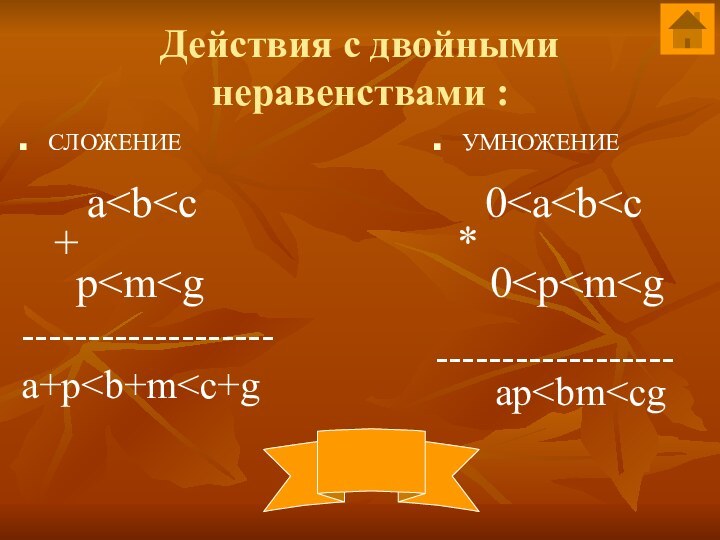
Действия с двойными неравенствами :
СЛОЖЕНИЕ
a
+
p
0
*
0
------------------
ap
Слайд 8
При доказательстве неравенств используются определения понятий больше или
меньше.
Пример:
Доказать, что
Решение:
Рассмотрим разность
Следовательно,
Слайд 9
Линейным неравенством называется неравенство вида ax+b>0 (или
ax+b0, то неравенство ax+b>0
равносильно неравенству
Если а
неравенство ax+b>0
равносильно неравенству
Слайд 10
Если ставится задача найти множество общих решений двух
или нескольких неравенств, то говорят, что нужно решить систему
неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Слайд 11
Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда
системы неравенств записывают в виде двойного неравенства.
Например, систему
3х-1>2,
3x-1<8
можно записать так: 2<3x-1<8
Слайд 12
Решение системы линейных неравенств с
одной переменной сводится
к следующим
случаям. Будем считать, что a
Слайд 13
Дидактический
материал
1. Найдите наибольшее целое число x, удовлетворяющее
неравенству:
2. Пусть
а
Слайд 14
3. Докажите, что:
а) если
, то ;
б) если , то ;
в) если , где а- неотрицательное число.
4. Пусть -3 а) (а+b);
b) 3a+2b.
5. Решить неравенство:
Слайд 15
7. Решите двойное неравенство:
8. Решить систему линейных неравенств:
Слайд 16
Контрольные вопросы по теме
1. Дайте определение неравенства.
2. Какие
виды неравенств вы знаете ?
3. Истинно ли высказывание:
4. Сформулируйте
свойства
неравенств.
5. Докажите, что если a>b и b>c, то
a>c.
6. Докажите, что если a0, то
ax>bx.
Слайд 17
7. Сформулируйте правила действий с неравенствами.
8. Что значит
решить неравенство, содержащее
переменную ?
9. Какие неравенства называются
равносильными?
10.Что значит решить систему неравенств ?