x
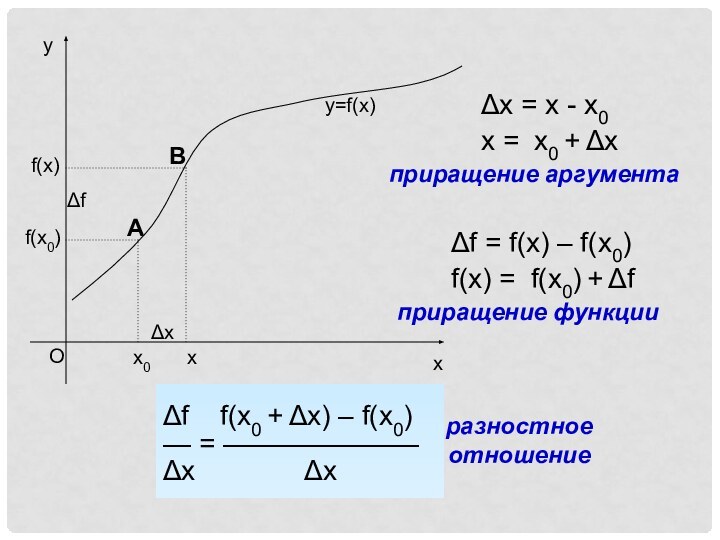
приращение аргумента
f = f(x) – f(x0)
f(x) = f(x0)
+ f приращение функции
f f(x0 + x) – f(x0)
— = ———————
x x
разностное отношение
А
В
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

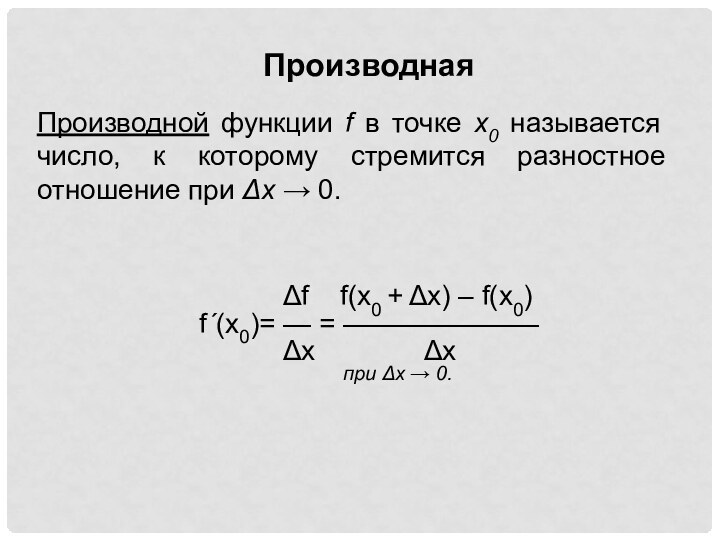





приращение функции
f f(x0 + x) – f(x0)
— = ———————
x x
разностное отношение
А
В
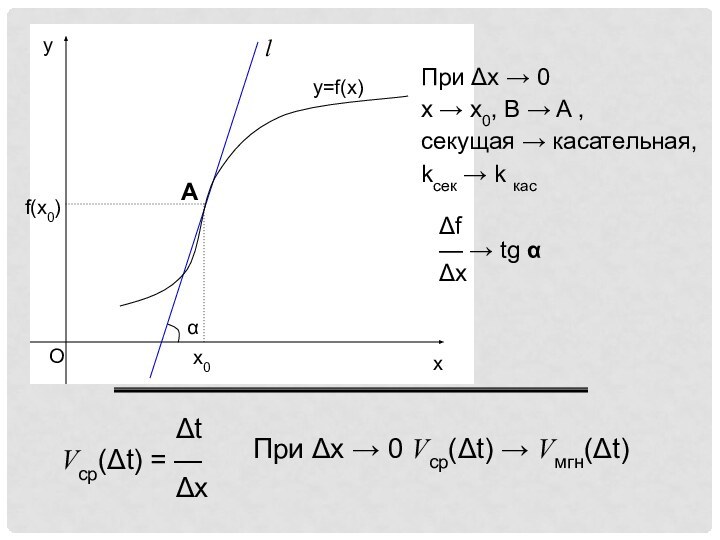
- средняя скорость движения тела за t
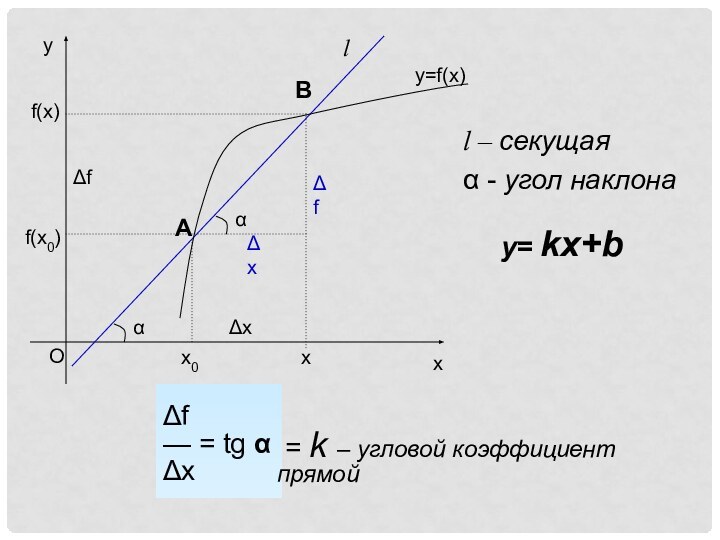
f
— tg
x
t
Vср(t) = —
x
При x 0 Vср(t) Vмгн(t)