- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Проверка статистических гипотез
Содержание
- 2. Критерий согласия хи-квадрат ПирсонаРазработан первоначально для дискретных
- 3. Статистика критерия:Является мерой близости теоретических вероятностей Рl
- 4. Для нахождения критической области необходимо по заданной
- 5. Подсчитываем значение статистики критерия и сравниваем его
- 6. Пять шагов проверки гипотезы1. Сформулировать нулевую H0
- 7. Простейшие параметрические гипотезыГипотезы о среднем значении гауссовской
- 8. Случай 1. Дисперсия известна и равна σ2Статистика критерияИмеет стандартное распределение
- 9. Скачать презентацию
- 10. Похожие презентации
Критерий согласия хи-квадрат ПирсонаРазработан первоначально для дискретных распределений:Статистический ряд:Нулевая гипотеза: исследуемая случайная величина имеет заданный закон распределения.







Слайд 2
Критерий согласия хи-квадрат Пирсона
Разработан первоначально для дискретных распределений:
Статистический
ряд:
Слайд 3
Статистика критерия:
Является мерой близости теоретических вероятностей Рl и
эмпирических (экспериментальных) частот vl
Имеет асимптотическое (при n -->oo )
распределение хи-квадрат.Число степеней свободы равно:
L-1, если распределение полностью задано.
L - 1 - r, если дополнительно оценивается r неизвестных параметров распределения.
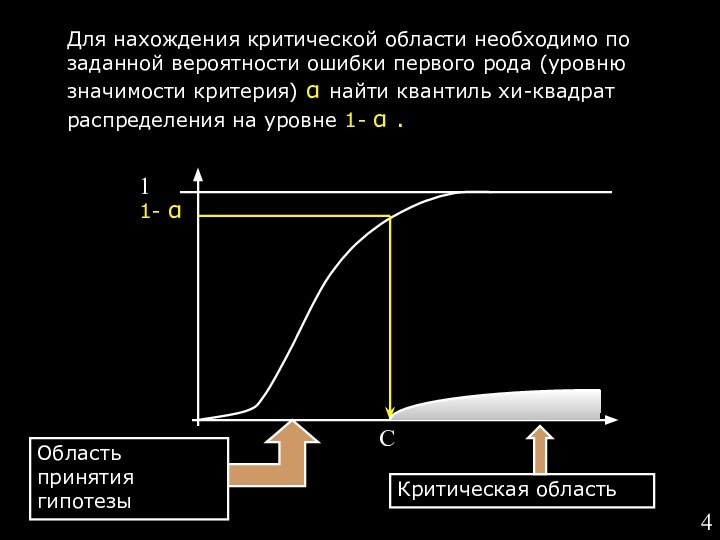
Слайд 4 Для нахождения критической области необходимо по заданной вероятности
ошибки первого рода (уровню значимости критерия) α найти квантиль
хи-квадрат распределения на уровне 1- α .Слайд 5 Подсчитываем значение статистики критерия и сравниваем его с
критической точкой. Если
То нулевая гипотеза отвергается.
В противном
случае она принимается на уровне значимости α Критерий легко приспосабливается и для непрерывных распределений путем их дискретизации.
Проверку гипотезы удобно совмещать с построением гистограмм.
Слайд 6
Пять шагов проверки гипотезы
1. Сформулировать нулевую H0 и
альтернативную H1 гипотезы.
2. Выбрать статистику критерия T(X) и
уяснить её закон распределения.3. Задать уровень значимости критерия. По таблицам квантилей распределения статистики найти критические точки и указать критическую область.
4. Подсчитать значение статистики критерия и проверить условие попадания в критическую область.
5. Сделать вывод о принятии нулевой или альтернативной гипотезы.
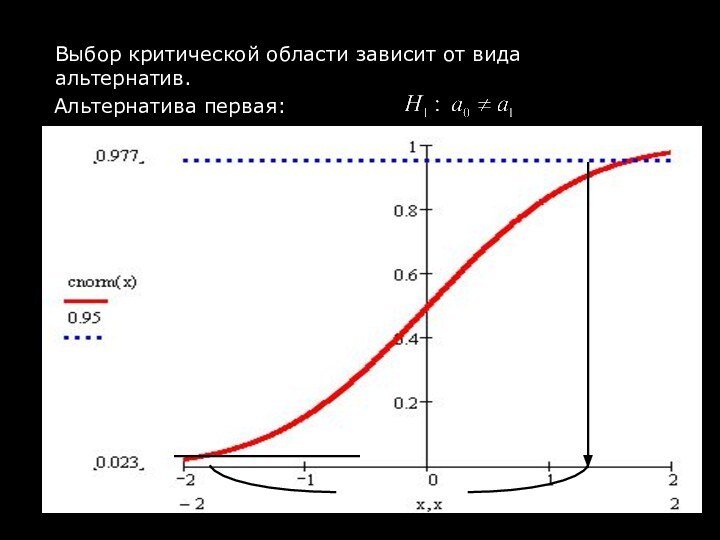
Слайд 7
Простейшие параметрические гипотезы
Гипотезы о среднем значении гауссовской случайной
величины
Дано: Проведено две серии независимых испытаний одинакового объема, по
результатам которых получены оценки математического ожидания a0 и a1. Проверить нулевую гипотезу: a0 = a1 .