Презентация на тему Прямая и обратная пропорциональные зависимости

мы можем рассчитать пройденное
им расстояние за любой отрезок времени:
Прямая

Прямо пропорциональные
величины

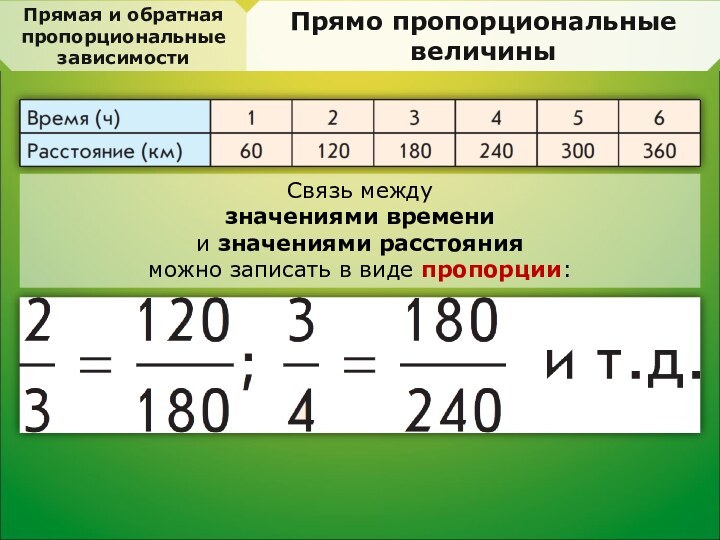
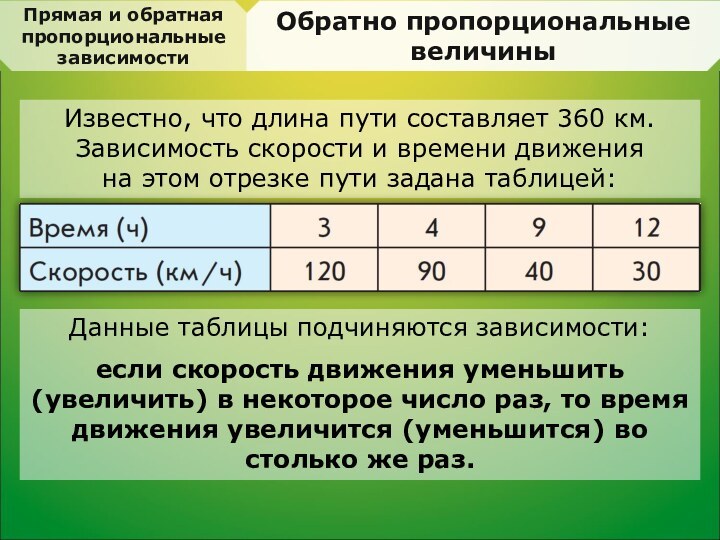
Данные этой таблицы подчиняются зависимости:

если время увеличить (уменьшить)
в некоторое число раз,
то и расстояние увеличится (уменьшится)
в это же число раз.

Данные этой таблицы подчиняются зависимости:
если время увеличить (уменьшить) в некоторое число раз, то и расстояние увеличится (уменьшится) в это же число раз.

то есть связь
между значениями времени и значениями расстояния можно записать в виде пропорции:

значениями расстояния
можно записать в виде пропорции:

две величины
связаны между собой так,

что с увеличением (уменьшением) одной

пропорциональны,
то отношение любых двух значений
первой величины равно отношению соответствующих

Примеры

– при постоянной скорости

– при постоянном времени

величин:
количество товара и его стоимость при постоянной цене
скорость и

длина прямоугольника и его площадь при постоянной ширине

объём параллелепипеда и площадь его основания
при постоянной высоте

величина дроби и её числитель при постоянном знаменателе

объём выполненной работы и затраченное на неё время
при постоянной производительности труда

производительность труда и объём выполненной работы
при постоянном времени

длина пути, проходимого равномерно движущимся телом,
и время его движения

машина прошла 120 км.
Требуется узнать, какое расстояние она пройдёт
за

Сначала узнаем, во сколько раз увеличится время движения:

6 : 2 = 3 раза.

Следовательно, путь так же увеличится в три раза:

120 · 3 = 360 (км).

Метод 1

машина прошла 120 км.
Требуется узнать, какое расстояние она пройдёт
за

Условие этой задачи можно записать так:

Одинаково направленные стрелки показывают,
что величины прямо пропорциональны, то есть отношение значений расстояния 120 : х
равно отношению
соответствующих значений времени 2 : 6.

Метод 2

машина прошла 120 км.
Требуется узнать, какое расстояние она пройдёт
за

Составим пропорцию: .

Метод 2

Теперь решим её:

величины»
говорят короче:
«пропорциональные величины».

величин
Если две величины
прямо пропорциональны,
то их частное –
величина постоянная,

и наоборот,

если

величин
Пример 1

величин
Пример 2

величин
Теперь ясно, почему при перечислении
пар прямо пропорциональных величин
обычно упоминается

Проанализировав пары известных
прямо пропорциональных величин,
можно обнаружить третью величину
(частное этих величин) и убедиться,
что она постоянна.

Проведём рассуждение,
доказывающее в общем виде утверждение
о постоянности частного
прямо пропорциональных величин*.

величин
Предположим, что величины a и b –
прямо пропорциональны.
Возьмём конкретное

Если a1 увеличить в k раз и получить
a2 = k · a1,
то b1 тоже увеличится в k раз и получится
b2 = k · b1.

величин
Сравним между собой частные


и убедимся, что они равны.
a1
b1
=
a2
b2
Действительно:


a2
b2
=
k ·

k · b2

=

a1

b1

И наоборот,
предположим, что частное величин a и b постоянно, скажем,

a

b

=

m

величин
Рассмотрим a1 и a2 – два значения величины a;

а

Убедимся, что если
a2 = k · a1,
то и b2 = k · b1.

Так как

a1

b1

a2

b2

=

m и

=

m, то .

a1

b1

=

a2

b2

Поменяем местами a1 и b2, получим

b2

b1

=

a2

a1

величин
Но поскольку


или b2 = k · b1,
в чём и

a2

a1

b2

b1

=

k, то и

=

k

Можно утверждать следующее:

Если величины a и b прямо пропорциональны, то они связаны между собой формулой


или a = m · b,
где m – некоторая постоянная величина.

a

b

=

m,

составляет 360 км. Зависимость скорости и времени движения
на этом

Данные таблицы подчиняются зависимости:

если скорость движения уменьшить (увеличить) в некоторое число раз, то время движения увеличится (уменьшится) во столько же раз.

Обратно пропорциональные
величины

значениями времени
можно записать в виде пропорции:

две величины
связаны между собой так,

что с увеличением (уменьшением) одной

отношение любых двух значений
первой величины равно обратному отношению соответствующих

Пример

– при неизменном расстоянии

Обратно пропорциональные
величины

величин:
количество товара и его цена
при одинаковой стоимости покупки
скорость и

производительность труда и время работы
при одинаковом объёме работы

число рабочих и время выполнения ими заданной работы
при одинаковой производительности труда всех рабочих

величина дроби и её знаменатель при постоянном числителе

часа на движение по некоторому участку пути со скоростью

Сначала узнаем, во сколько раз увеличится скорость движения:

100 : 50 = 2 раза.

Следовательно, время движения уменьшится в 2 раза
и станет равным:

2 : 2 = 1 ч.

Метод 1

можно записать так:
Противоположно направленные стрелки показывают,
что величины обратно пропорциональны,

Пример
Машина затратила 2 часа на движение по некоторому участку пути со скоростью 50 км/ч. Требуется узнать, за какое время она пройдёт этот же участок пути, если её скорость будет 100 км/ч.

Метод 2

.

Найдём неизвестный

Пример
Машина затратила 2 часа на движение по некоторому участку пути со скоростью 50 км/ч. Требуется узнать, за какое время она пройдёт этот же участок пути, если её скорость будет 100 км/ч.

Метод 2

величин
Если две величины
обратно пропорциональны,
то их произведение –
величина постоянная,

и наоборот,

если

S –
обратно пропорциональные величины.

Рассмотрим произведение этих величин: v

Прямая и обратная пропорциональные зависимости

Характеристическое свойство обратно пропорциональных величин

Пример 1

той же площадью S и убедимся, что длины их

Прямая и обратная пропорциональные зависимости

Характеристическое свойство обратно пропорциональных величин

Пример 2

величин
Теперь ясно, почему при перечислении
пар обратно пропорциональных величин
обычно упоминается

Проанализировав пары известных
Обратно пропорциональных величин,
можно обнаружить третью величину
(частное этих величин) и убедиться,
что она постоянна.

Проведём рассуждение,
доказывающее в общем виде утверждение
о постоянности произведения
обратно пропорциональных величин*.

величин
Предположим, что величины a и b –
Обратно пропорциональны.
Возьмём конкретное

Если a1 увеличить в k раз и получить
a2 = k · a1,
то b1 уменьшится в k раз и получится

b2 =

b1

k

величин
Убедимся, что произведения

a1 · b1 и a2 · b2

равны.
Действительно:


a2

=

k · a1 · b1

k

И наоборот,
предположим, что произведени величин a и b постоянно, скажем,
a · b = n.

b1

k

=

a1 · b1

величин
Рассмотрим a1 и a2 – два значения величины a;

а

Убедимся, что если
a2 = k · a1,

Так как
a1 · b1 = n и a2 · b2 = n, то a1 · b1 = a2 · b2.

b1

k

то b2 = .

величин
Тогда имеем:


в чём и требовалось убедиться.
a1 · b1
a2
=
Можно утверждать

Если величины a и b –
обратно пропорциональны, то они связаны между собой формулой
a · b = n,


где n – некоторая постоянная величина.

n

b

=

или a ,

b2=

a1 · b1

k · a1

=

b1

k

величина увеличивается,
когда увеличивается другая,
то это не обязательно означает,
что они

С увеличением одного из слагаемых
Увеличивается и сумма,
однако было бы ошибочно считать,
что сумма прямо пропорциональна этому слагаемому, так как они увеличиваются не в одинаковое число раз.

Пример