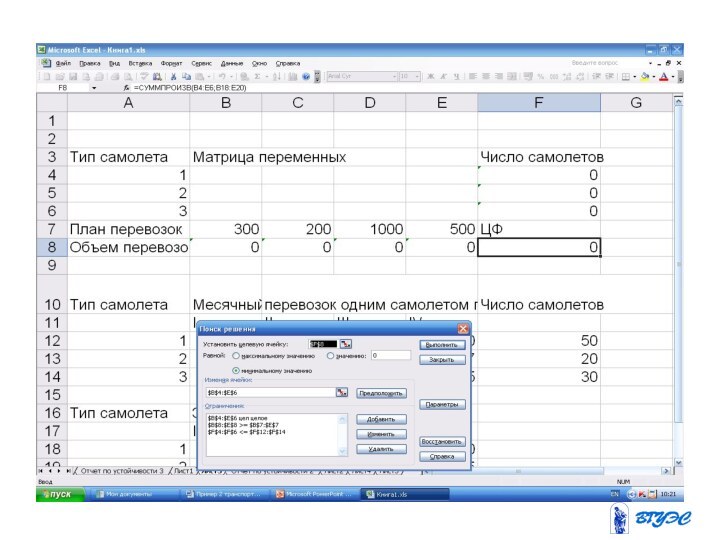
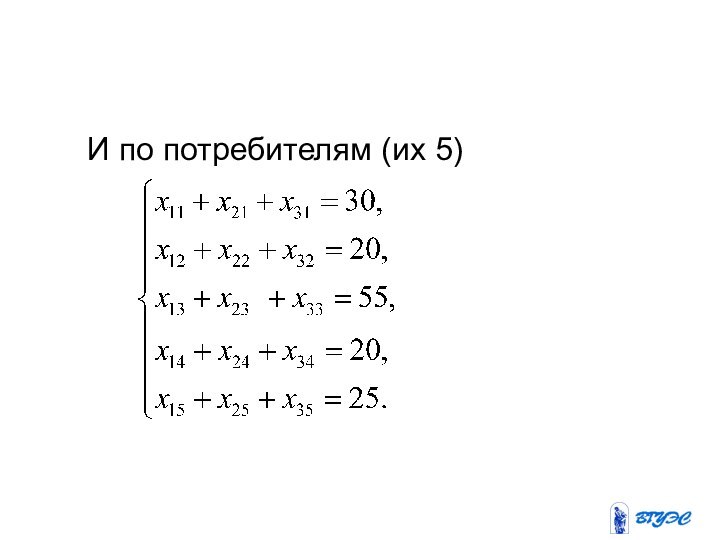т. к. ее
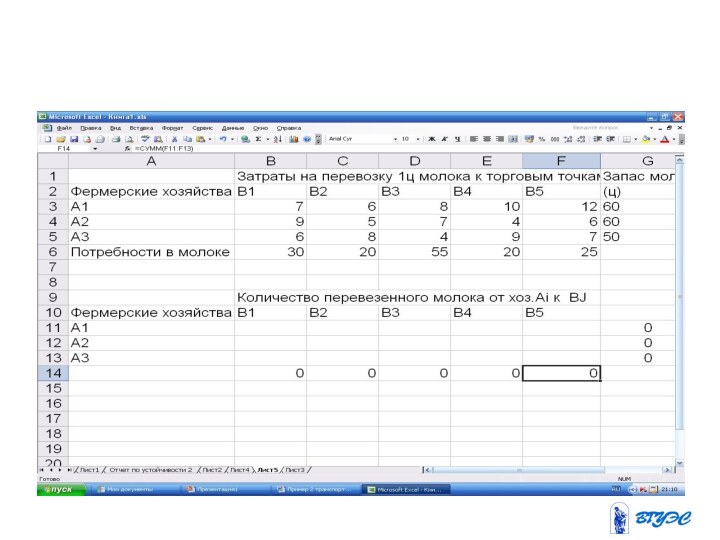
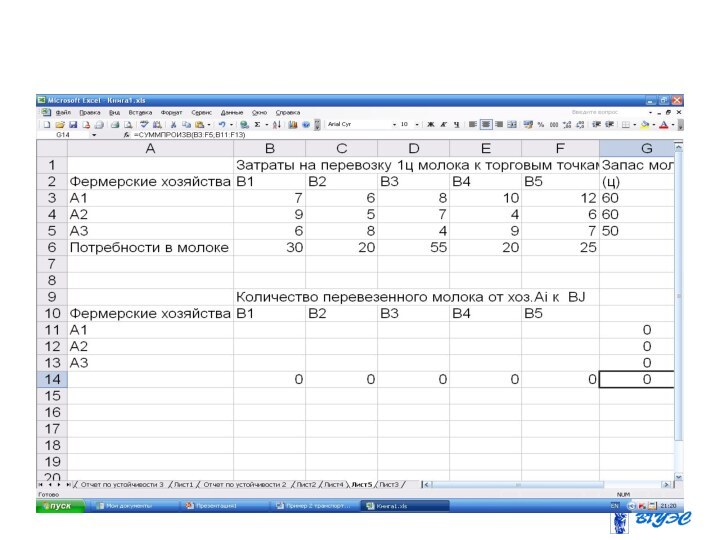
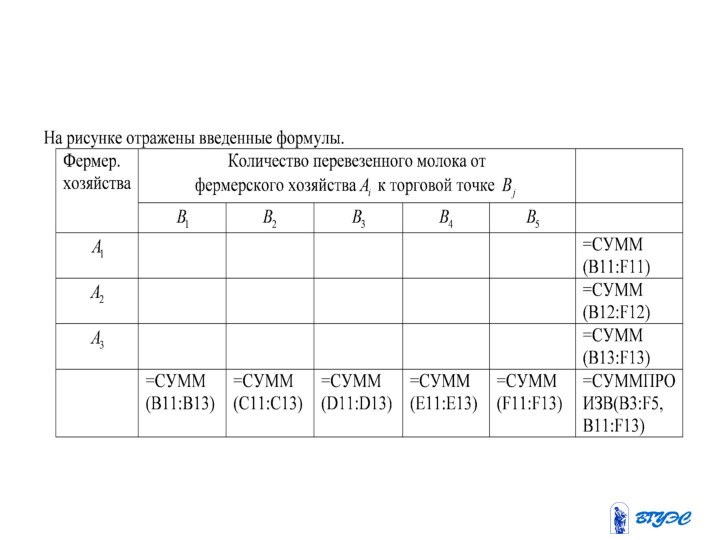
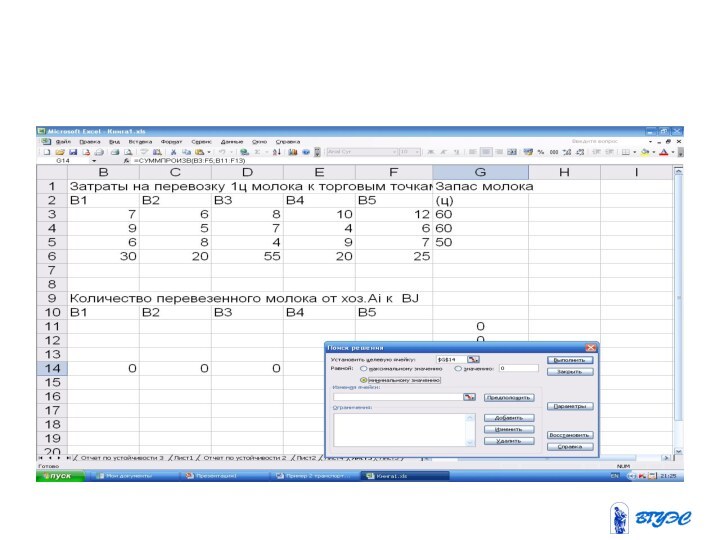
математическая модель сводится к минимизации
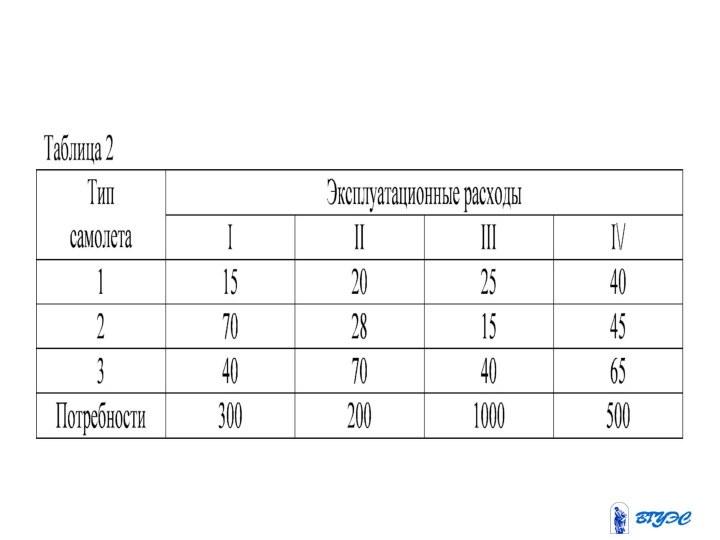
целевой функции, выражающей суммарные затраты на перевозку всего грузапри ограничениях
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть