рассекают вспомогательной секущей плоскостью Г
2. Находят линию пересечения вспомогательной
плоскости с каждым из объектов4. Выбирают следующую секущую плоскость и повторяют алгоритм
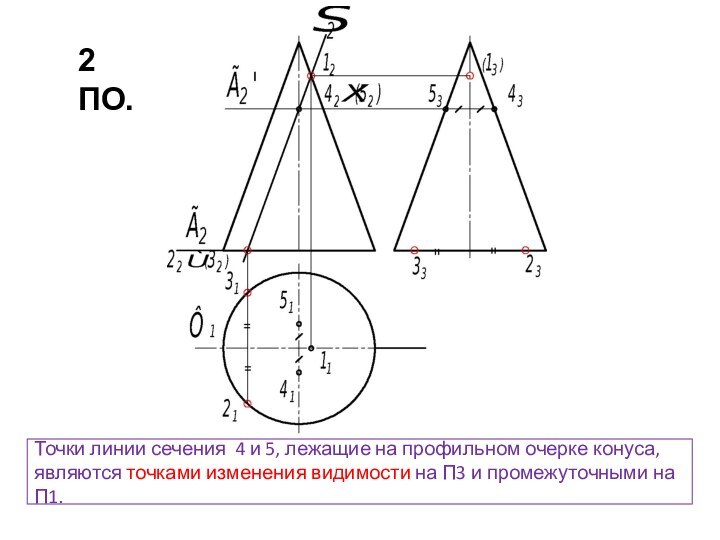
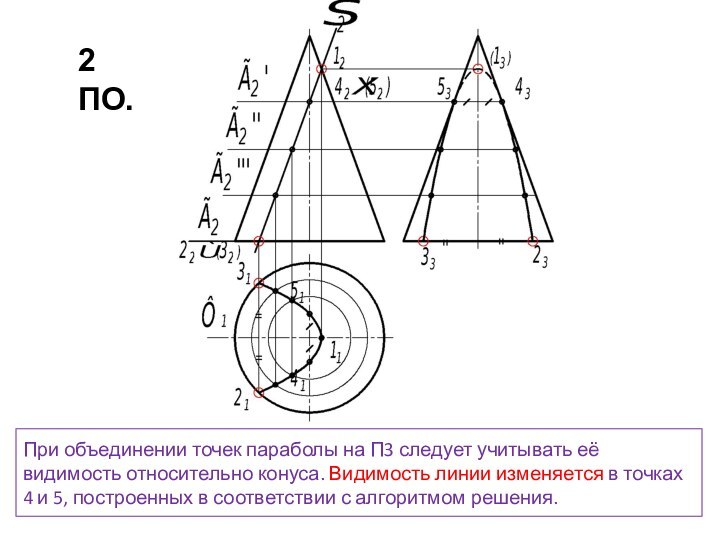
5. Полученные точки соединяют с учетом видимости искомой линии пересечения
a b Ю A,B
3. На полученных линиях пересечения определяют общие точки, принадлежащие заданным поверхностям