Слайд 2
Введение
Математика – настоящее волшебное царство .
А цифры , числа , геометрические фигуры, если вы
сильно захотите , могут превратиться в удивительные сказочные персонажи .
Первые математические понятия ребёнок узнаёт из сказок: 1) числа (Белоснежка и семь гномов , Три поросёнка) , 2) счёт ( Рукавичка), 3) сравнение ( Три медведя, Дюймовочка), 4)геометрические фигуры ( Колобок )
Математика ум в порядок приводит ,
Математика неизвестное находит ,
Математика дарит нам радости чувства ,
Математика - это наука – искусство.
Слайд 3
Цель работы:
- Доказать, что такое понятие, как сказки
в математике, имеет право на существование.
- Привести конкретные примеры
взаимосвязи математики и сказок.
- Доказать, что математика и сказки могут существовать вместе, не противореча друг другу.
План:
- Вступление
-Числительные в сказках
-Математические задачи в сказках
-Математики-литераторы
Литературно-математическая викторина
-Заключение
Слайд 4
Сказки в математике. Звучит необычно и как-то странно.
Со
сказками мы привыкли сталкиваться на уроках литературы. Сказки –
это приключения, мы несерьезно относимся к ним.
А математика – царица всех наук. С начальной школы нас приучают быть внимательными, трудолюбивыми и серьезными с этой особой. Мы привыкли, что математика – наука сухая и не всегда интересная, говорящая на своем языке формул, уравнений, рассуждений, доказательств, графиков…Но ведь это совсем не значит, что слова «сказка» и «математика» не могут стоять рядом. Конечно, могут!
Слайд 5
Числительные в сказках
Присутствие чисел в сказках наблюдается повсюду
и почти всегда они выступают как священные и глубоко
символические. Число один встречается в русской традиции крайне редко. Однако образ Аники воина, который выезжает в Чисто Поле , чтобы биться с врагом одному, а также символ копья и единорога, встречающиеся в текстах летописей и древних преданий говорят об обратном. Число два олицетворяет идею чета и нечета, выражает собой соотношения правого и неправого начал. Славянскую сказку пронизывает идея борьбы таких начал как Жизнь и Смерть , живая и мертвая Правда и Кривда.
Гораздо чаще в русской сказке и фольклоре говорят о числе семь. Это и семь богов древнерусского пантеона, и бог Семаргл, явно ведущий свое имя от числа 7, и семь небес, и многие другие семеричные символы, разбросанные по многочисленным легендам, сказкам и преданиям. "7 - число человеческое - (семь отверстий в человеческой голове), семь возрастов, семь добродетелей.
Слайд 6
Любимое сказочное число
Кто из нас не помнит знаменитого
сказочного зачина: « За тридевять земель в тридевятом царстве жили-были…» И
кто из нас, зачитываясь в детстве сказками. Не сталкивался с таинственным числом « три».
У крестьянина три сына:
Старший умный был детина,
Средний сын - и так и сяк,
Младший вовсе был дурак.
И вот этого младшего, любимого всеми Иванушку-дурочка, судьба всегда трижды испытывает.
А пословицы и поговорки? Ведь буквально пересыпаны числом три: «в трех соснах», «в три ручья», «с три короба».
Так от куда оно взялось это магическое «три»?
Любопытно, что число 3 рассматривали не только как счастливое («бог троицу любит»), но и как несчастливое («треклятый»).
Число 9 находится в непосредственной связи и зависимости от числа три. От 3 х 3= 9 делается шаг к 3 х 9 = 27. Это число тоже имеет магическую силу. От него и идет знаменитое сказочное «за тридевять земель».
Слайд 7
Особое число
Самым, пожалуй, загадочным и даже волшебным числом

в математике является число ноль. С его особыми свойствами
мы сталкиваемся уже в начальной и средней школе. На ноль нельзя делить. При первом знакомстве с числовой прямой, выясняется, что ноль не тождественен пустому множеству. Это число не только имеет свою координату на числовой прямой, но из него берут начало системы отсчёта. Можно сказать, что ноль является пограничной точкой, разделяющей положительные и отрицательные числа, направления вверх и вниз, вправо и влево, вперёд и назад .В волшебной сказке мы встречаемся с героиней, чьи характеристики напоминают нам характеристики этого числа. Она всегда живёт на границе двух миров, являясь как бы дверью между ними. Избушка Бабы Яги никогда не является составной частью тех миров, которые она разделяет, но всегда лишь – границей.Итак, избушка Бабы Яги – это точка посвящения. Недостойные либо не допускаются, либо гибнут. Достойные могут пересечь эту границу и вернуться обратно в материальный мир живыми..
Слайд 8
О НУЛЕ
Когда-то многие считали,
Что нуль не значит ничего.
И
как ни странно, полагали,
Что нуль совсем не есть число.
Но
на оси средь прочих чисел
Он все же место получил.
И все действительные числа
На два разряда разделил.
Коль нуль к числу ты прибавляешь,
Иль отнимаешь от него,
В ответе тотчас получаешь
Опять то самое число.
Попав, как множитель, средь чисел
Он сводит мигом все на нет.
И потому в произведеньи
Один за всех несет ответ.
А относительно деленья
Во-первых, нужно помнить то,
Что уж давно в научном мире
Делить на нуль запрещено.
Причина всем ведь очевидна,
А состоит причина в том,
Что смысла нет в таком деленьи
Противоречье в нем само.
Слайд 9
Математические сказки
.“ Жили – были три дроби: 3/6,
1/2 и 6/12. Они были сестрами-близнецами, но об этом
не знали. Однажды у дроби 3/6 было день рождения. И она пригласила своих подружек- дробей: 1/2 и 6/12. Пригласила и друга: правило по сокращению дробей. Подружки преподнесли свои подарки имениннице и с нетерпением ждали, а что же подарит правило? Друг сказал: “Мой подарок будет таким: я тебя сокращу”. И прочитало свое заклинание-правило: “Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби”. И тогда дробь 3/6 стала дробью 1/2. Подружка 6/12 тоже попросила, правило сократило и ее на 6, и она тоже стала дробью 1/2. А третью подружку, дробь 1/2, правило не смогло сократить, потому что эта дробь была несократимой. И поняли подружки, что они сестры-близнецы. (“Сокращение дробей”, Хамматов Руслан, 6 класс).
Слайд 10
ТРЕУГОЛЬНИК И КВАДРАТ
Жили-были два брата:
Треугольник с квадратом
Старший
— квадратный
Добродушный, приятный
Младший — треугольный,
Вечно недовольный.
Стал расспрашивать квадрат:
— Почему
ты злишься, брат?
Тот кричит ему: — Смотри,
Ты полней меня и шире,
У меня углов лишь три,
У тебя же их четыре!
Но квадрат ответил: — Брат!
Я же старше, я — квадрат:
Я сказал еще нежней:
— Неизвестно, кто нужней!
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя сказал:
— Приятных я тебе Желаю снов!
Знать, ложился — был квадратным,
А проснешься без углов!
Но наутро младший брат
Страшной мести был не рад.
Поглядел он — нет квадрата,
Онемел, стоял без слов...
Вот так месть! Теперь у брата
Восемь новеньких углов.
Слайд 11
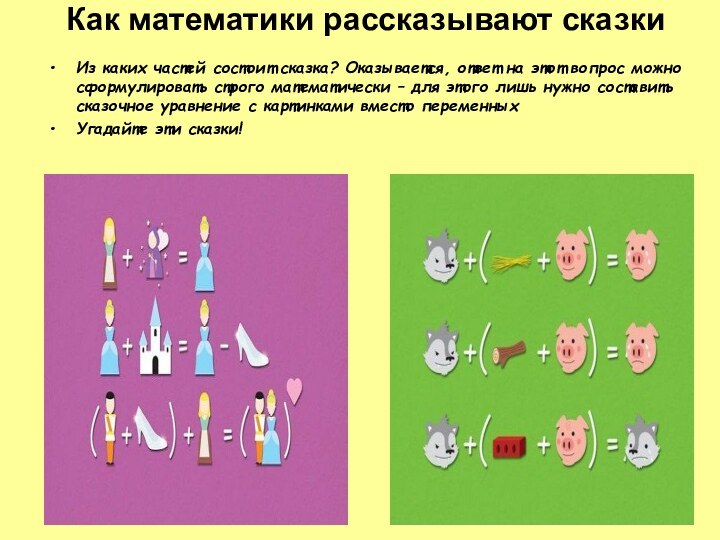
Как математики рассказывают сказки
Из каких частей состоит сказка?
Оказывается, ответ на этот вопрос можно сформулировать строго математически
– для этого лишь нужно составить сказочное уравнение с картинками вместо переменных
Угадайте эти сказки!
Слайд 12
Задача из сказки
Одна женщина отправилась в сад
собрать яблоки. Чтобы выйти из сада, ей нужно было
пройти через 4 двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину собранных ею яблок. Дойдя до второго стражника, женщина отдала ему половину оставшихся яблок. Так же она поступила и с третьим стражником, а когда она поделилась яблоками со стражником у четвертых дверей, то у нее осталось лишь 10 яблок. Сколько яблок она собрала в саду?
Задача из сборника сказок «1001 ночь»
Решение: 10х2х2х2х2 = 160.
Слайд 13
Математики - литераторы
Почему среди математиков оказывается так много
талантливых писателей? Казалось бы, буйная фантазия и строгая цифра
- вещи несовместимые, присущие антиподам. Но как объяснить феномен Льюиса Кэрролла, Александра Солженицына, Софьи Ковалевской, Александра Сухово-Кобылина, Айзека Азимова, нашего современника Александра Кабакова, не говоря о фигурах меньшей известности? Слишком много имен, чтобы это было случайностью. В канадском университете Ватерлоо проведено исследование, которое доказывает, что вслед за проявившимися в детстве способностями хорошего рассказчика обнаруживаются и яркая математическая одаренность.
Слайд 14
ПУШКИН И МАТЕМАТИКА
Прослеживается неразрывная связь Пушкина с математикой.

Первые знания по математике Пушкин получил, скорее всего, в
детстве от часто сменяющихся французов-гувернеров.
В лицее математику изучали основательно: в программу математики входили арифметика, геометрия, прикладная математика, чистая математика, даже математика с дифференциалами и интегралами. Но, Пушкин в лицее “ленился и отставал”. Тем не менее, я считаю, что Пушкин получил неплохую математическую подготовку.
Поэтому впоследствии в его творчестве находятся некоторые интересные моменты, связанные с математикой
Кое-какие данные, связанные с расчетами имеются в сказке “ О царе Салтане”. Просчитав возможное расстояние от царства Салтана до острова Буяна, до города-дворца, обоснованного князем Гвидоном, до которого могла доплыть бочка с царицей и его сыном, сделал вывод, что царица с сыном находились на достаточно большом расстоянии, что весть о диковинках этого города доходила до царя Салтана проезжающих купцов не так быстро и не так долго. Значит, поэзия Пушкина базировалась на глубоком знании предмета, охвате всех его сторон и оказалась достовернее упрощенных примитивных математических моделей.
Значит, слова “Сказка ложь, да в ней намек, добрым молодцам урок”- непустые слова в сказках Пушкина. Кроме того, крылатые слова Пушкина “В геометрии нужно вдохновение, как и в поэзии”, “Поверил я алгеброй гармонию” и др. имеют глубокий математический смысл
Слайд 15
А.П. Чехов "Задачи сумасшедшего математика"
За мной гнались

30 собак, из которых 7 были белые, 8 серые,
а остальные черные. Спрашивается, за какую ногу укусили меня собаки, за правую или левую?
Куплено было 20 цибиков чая. В каждом цибике было по 5 пудов, каждый пуд имел 40 фунтов. Из лошадей, везших чай, две пали в дороге, один из возчиков заболел, и 18 фунтов рассыпалось. Фунт имеет 96 золотников чая. Спрашивается, какая разница между огуречным рассолом и недоумением?
Английский язык имеет 137856738 слов, французский в 0,7 раз больше. Англичане сошлись с французами и соединили оба языка воедино. Спрашивается, что стоит третий попугай и сколько понадобилось времени, чтобы покорить сии народы?
В среду 17-го июня 1881 года в 3 часа ночи должен был выйти со станции А поезд железной дороги, с тем, чтобы в 11 час. вечера прибыть па станцию В; но при самом отправлении поезда получено было приказание, чтобы поезд прибыл на станцию В в 7 часов вечера. Кто продолжительнее любит, мужчина или женщина?
Моей теще 75 лет, а жене 42. Который час?
Слайд 16
Литературно – Математическая викторина
¥ Какому
русскому поэту принадлежат эти математические строки: «Мы почитаем всех
нулями, а единицами себя»?
(А.С. Пушкину.)
¥ Какой пушкинский герой говорил:
«... Поверил
Я алгеброй гармонию...»
(Сальери в произведении «Моцарт и Сальери».)
¥ Чьи это строки?
«Мы любим всё - и жар холодных чисел,
И дар божественных видений,
Нам внятно всё - и острый галльский смысл,
И сумрачный германский гений...»
(А. Блок «Скифы».)
Слайд 17
¥ Какой поэт воспел числа?
«Вам поклоняюсь, вас желаю,
числа!
Свободные, бесплотные, как тени,
Вы радугой связующей повисли
К раздумиям с
вершины вдохновенья!»
(В. Брюсов «Числа».)
¥ Какие книги написал профессор математики, логик Чарльз Лютвидж Доджсон, он же Льюис Кэррол?
(«Алиса в стране Чудес», «В Зазеркалье».)
¥ Что изобрёл Льюис Кэрролл как математик?
(Способы проверки делимости чисел на 17 и 19. Приём запоминания ряда цифр бесконечной дроби 3,14..., благодаря которому он мог записать число p до 71 знака после запятой. Предвосхитил некоторые идеи математической логики.)
¥ Сколько жителей было в деревушке Флорида штата Миссури, в которой родился будущий писатель Марк Твен, если в автобиографии писатель говорит: «Я увеличил население ровно на один процент. Не каждый исторический деятель может похвастаться, что сделал больше для родного города»?
(100 человек.)
Слайд 18
¥ В повести И.С. Тургенева «Муму» сказано, что

Герасим был «двенадцать вершков роста». Один вершок примерно равен
4,4 см. Получается, что рост Герасима был около 53 см, что противоречит описанию могучей фигуры героя в повести. Разве у Тургенева было плохо с математикой?
(Нет. Просто во времена Тургенева указывалось, на сколько вершков человеческий рост превышает 2 аршина. Один аршин равен 71 см, поэтому настоящий рост Герасима 195 см.)
¥ Какое число получило имя Шахерезады (Шехерезады) и каковы его замечательные свойства?
(1001 - число Шахерезады, оно виднеется в заглавии бессмертных сказок «Тысяча и одна ночь». С точки зрения математики число 1001 обладает целым рядом интереснейших свойств:
а) Это самое малое натуральное четырёхзначное число, которое можно представить в виде суммы кубов двух натуральных чисел: 1001 = 103+13;
б) Число 1001 состоит из 77 злополучных чёртовых дюжин (1001 = 77х13), из 91 одиннадцаток или из 143 семёрок (вспомним, что число 7 считалось магическим числом);
в) На свойствах числа 1001 базируется метод определения делимости числа на 7, на 11 и на 13.)
¥ Какой прозаический жанр является средним арифметическим рассказа и романа?
(Повесть.)
Слайд 19
¥ Рекордсменом среди писателей с результатом 27000 является

Л.Н. Толстой, а на втором месте - А.С. Пушкин
с 24000. По какой номинации?
(По запасу используемых слов.)
¥ По подсчётам учёных, герои произведений Шекспира произносят это слово 2259 раз. Что это за слово?
(«Любовь».)
¥ «Математический» детский фольклор - это ... Что?
(Считалки, считалочки.)
¥ Какая «литературная величина» произведения бывает и положительной, и отрицательной?
(Герой, персонаж литературного произведения.)
¥ Какую линию можно найти в литературном произведении?
(Сюжетную линию.)
¥ Что любят делать «делимым» у неубитого медведя, согласно русской пословице?
(Шкуру. Делить шкуру неубитого медведя.)
¥ Какой математический закон, известный всем с младших классов, стал популярной пословицей?
(От перемены мест слагаемых сумма не изменяется. Это переместительный, или коммутативный закон, свойство сложения и умножения, выражаемое формулами a + b = b + a, ab = ba.)
¥ Кто выше: сказочный россиянин-коротышка Мужичок-с-ноготок или Дюймовочка?
(Дюймовочка, ведь рост Дюймовочки 2,54 см, что больше размера ноготка.)
Слайд 20
Это ложь, что в науке поэзии нет.
В отраженьях
великого мира
Сотни красок со звуков уловит поэт
И повторит волшебная
лира.
За чертогами формул, забыв о весне,
В мире чисел бродя, как лунатик,
Вдруг гармонию выводов дарит струне,
К звучной скрипке, прильнув, математик.
Настоящий учёный, он тоже поэт,
Вечно жаждущий знать и предвидеть.
Кто сказал, что в науке поэзии нет?
Нужно только понять и увидеть.
Бромлей.
Заключение