- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Способы решения квадратных уравнений
Содержание
- 2. Тема:
- 3. Цели:Обобщить, систематизировать и расширить знания по теме «Квадратные уравнения»
- 4. Ход исследования:Определение квадратного уравнения.История квадратного уравнения.Решение квадратного
- 5. Определение квадратного уравнения.Квадратным уравнением называется уравнение вида
- 6. История квадратного уравнения. В третьем
- 7. История квадратного уравнения. Общий метод
- 8. История квадратного уравнения. Теорию квадратных уравнений
- 9. Решение квадратного уравнения через дискриминант.
- 10. История теоремы Виета.Франсуа Виет(1540-1603) Именно
- 11. Решение квадратного уравнения через теорему Виета.
- 12. Решения квадратных уравнений через
- 13. Решение квадратных уравнений через теорему №1.
- 14. Решение квадратного уравнения через теорему №2 ax²
- 15. Скачать презентацию
- 16. Похожие презентации
Тема: Способы решения квадратных уравнений.











Слайд 4
Ход исследования:
Определение квадратного уравнения.
История квадратного уравнения.
Решение квадратного уравнения
через дискриминант.
История теоремы Виета.
Решение квадратного уравнения через теорему Виета.
Решения квадратного уравнения через D1.Решение квадратного уравнения через теоремы №1 и №2 .
Слайд 5
Определение квадратного
уравнения.
Квадратным уравнением называется уравнение вида ax²+bх+с=0, где
х – переменная, a, b, с – некоторые числа,
причем a≠0.Числа a, b, с – коэффициенты квадратного уравнения. Число a – первый коэффициент, b – второй коэффициент, с – свободный член.
Если в квадратном уравнении ax²+bx+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется неполным квадратным уравнением.
Квадратное уравнение, в котором коэффициент a=1 называется приведенным квадратным уравнением
Слайд 6
История квадратного
уравнения.
В третьем веке до
н. э. Евклид отвел геометрической алгебре в своих «Началах»
всю вторую книгу, где собран необходимый материал для решения квадратных уравнений
Слайд 7
История квадратного
уравнения.
Общий метод решения квадратных
уравнений был открыт индийскими математиками. Так, в 12 веке
н.э. индийский математик Бхаскара для общего уравнения ax2+bx+c=0 нашел решение в виде:X=
Причем отрицательных корней он в расчет не принимал.
Слайд 8
История квадратного
уравнения.
Теорию квадратных уравнений хорошо разработал
аль -Хорезми, который дал шесть видов квадратных уравнений:
x2
=b xX2 = c
b x2 = c
X2 + b x = c
X2 + c = b x
b x + c = x2
Слайд 9
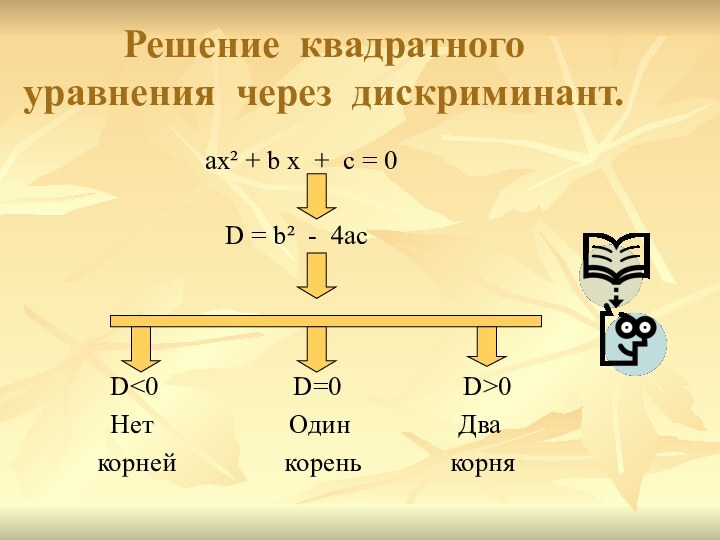
Решение квадратного
уравнения через дискриминант.
ax² + b x + c = 0
D = b² - 4ac
D<0 D=0 D>0
Нет Один Два
корней корень корня
Слайд 10
История теоремы Виета.
Франсуа Виет(1540-1603)
Именно этим
французским математиком впервые были введены буквенные обозначения. До этого
пользовались громоздкими словесными формулировками.пример: «Квадрат и число 24 равны одиннадцати корням» или x2 + 24 = 11x
Формулы, выражающие зависимость корней от его коэффициентов, были выведены Виетом в 1591г.
Слайд 12
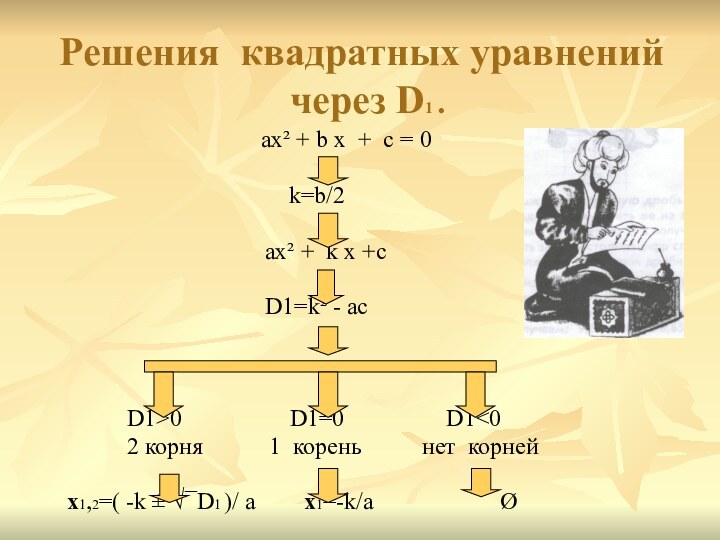
Решения квадратных уравнений
через D1 .
ax² + b x + с = 0
k=b/2
ax² + k x +c
D1=k² - ac
D1>0 D1=0 D1<0
2 корня 1 корень нет корней
x1,2=( -k ± √¯D1 )/ a x1=-k/a Ø
Слайд 13
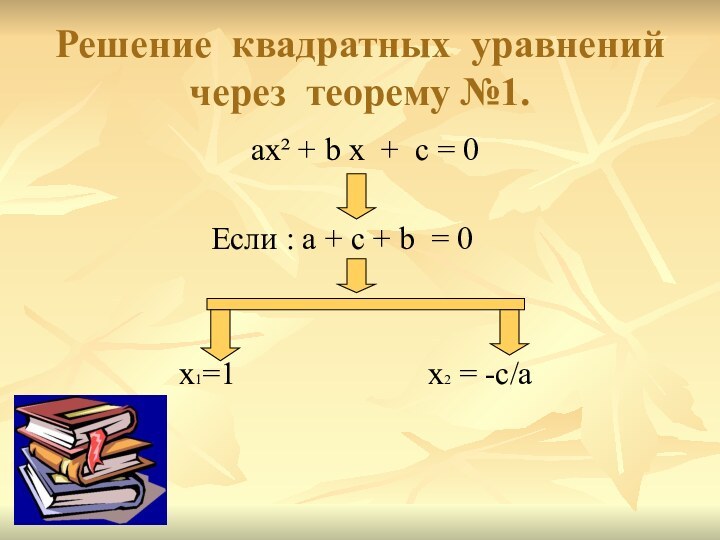
Решение квадратных уравнений
через теорему №1.
ax² + b x + c = 0
Если : a + с + b = 0
x1=1 x2 = -c/a
Слайд 14
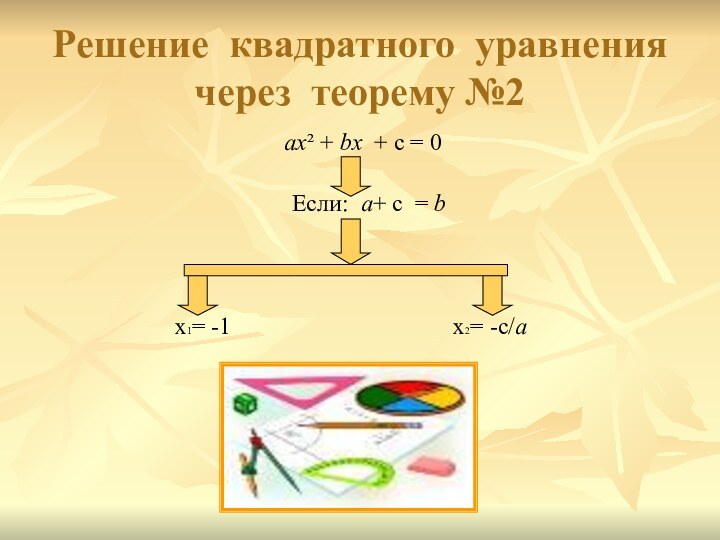
Решение квадратного уравнения через теорему №2
ax² +
bx + с = 0
Если: a+ с = b
x1= -1 x2= -с/a





























