Презентация на тему Степенная функция,её свойства и график

и т. д.
Все эти функции являются частными случаями

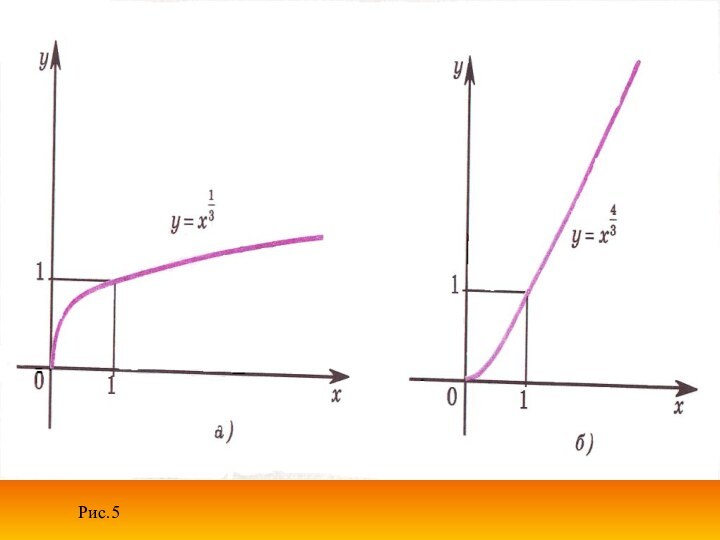
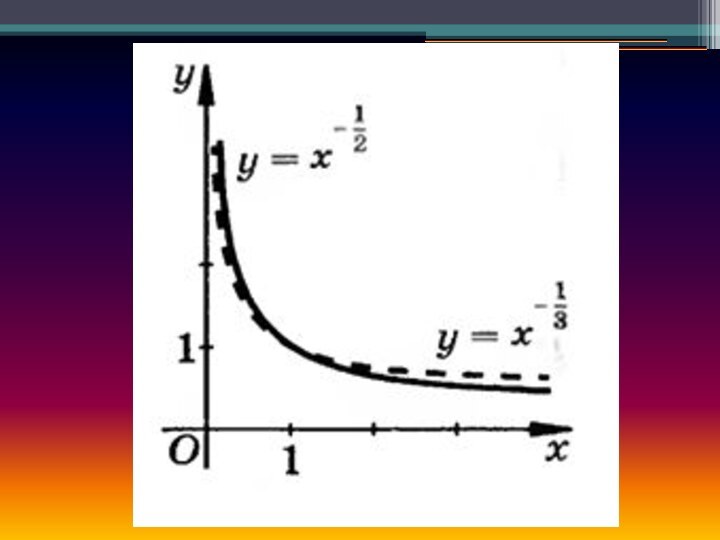
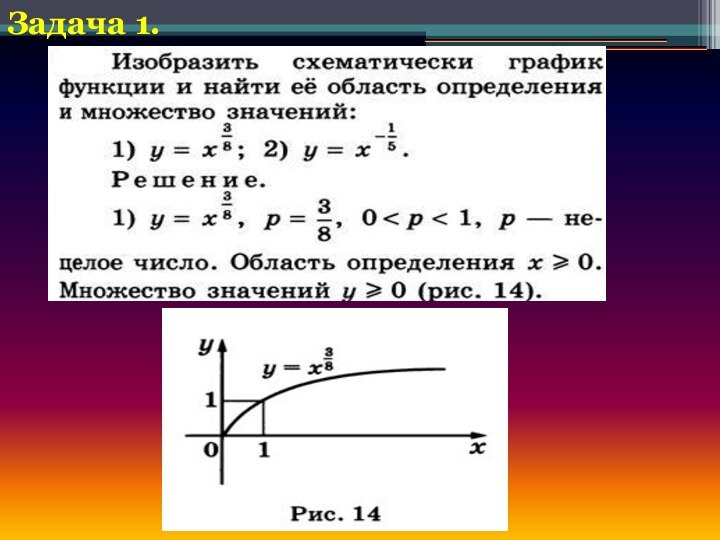
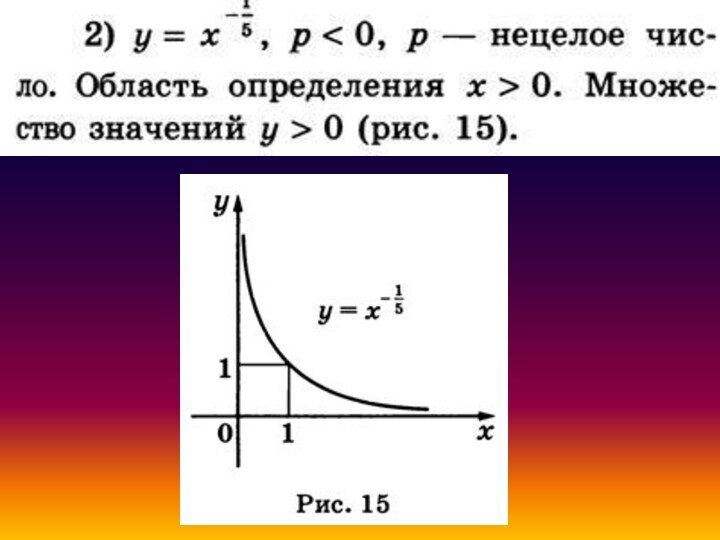
степенной функции,
т. е. функции у = хР, где р - заданное действительное число.

этом случае степенная функция у = х2n, где n

- натуральное число, обладает следующими свойствами:
- область определения - все действительные числа, т. е. множество R ;
- множество значений - неотрицательные числа, т. е. y≥ 0;
функция у=х2n четная, так как (-х)2n = х2n;
- функция является убывающей на промежутке x≥O и возрастающей на промежутке x≤ O.

График функции у = хР имеет такой же вид, как, например, график функции у = х4 (рис. 1).

этом случае степенная функция y=х2n-1, где 2n-1 - натуральное

число, обладает следующими свойствами:
- область определения - множество R;
- множество значений - множество R;
Функция y=х2n-1 нечетная, так как
(-х)2n-1=- х2n-1;
- функция является возрастающей на всей действительной оси.
График функции y=х2n-1 имеет такой же вид, как, например, график функции y=х3(рис. 2).

х
2n-1

свойствами:
- область определения - множество R, кроме х=

0;
- множество значений - положительные числа у>0;
- Функция y=х2n- четная, так как (-х)2n =х2n;
функция является возрастающей на промежутке х<0 и убывающей на промежутке х>0.
График функции y=х 2nимеет такой же вид, как, например, график функции y=х-2(рис.3).

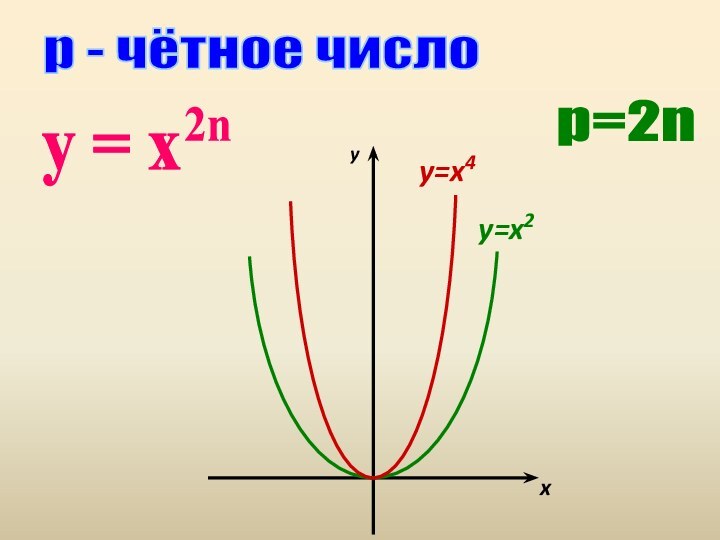
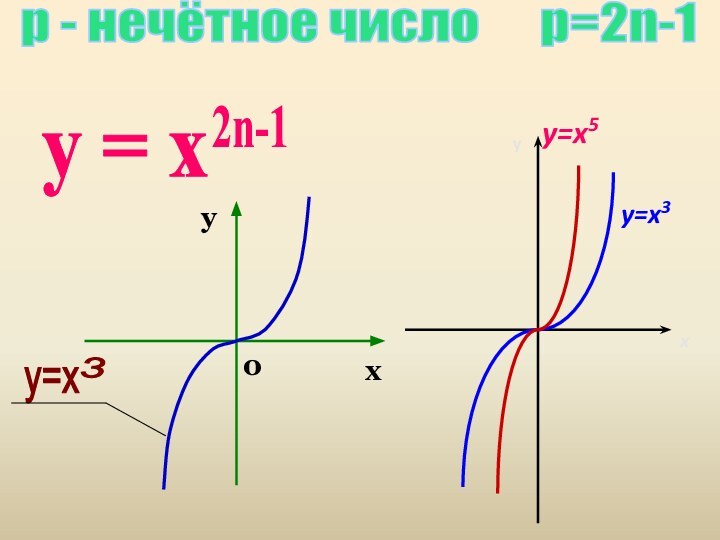
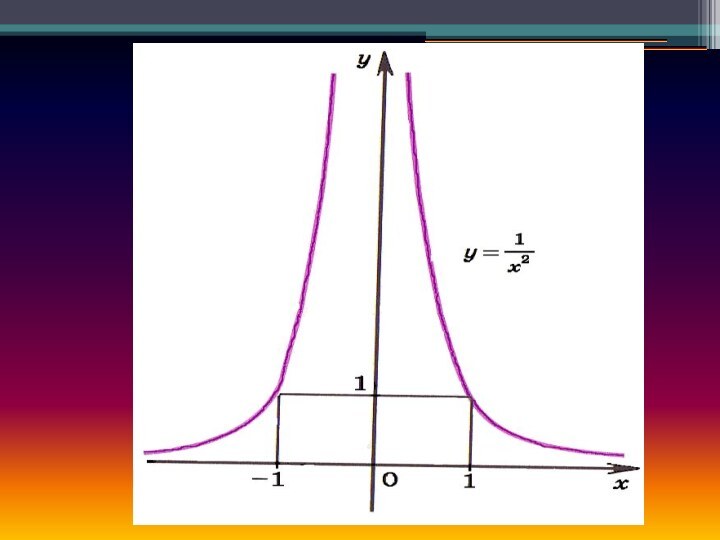
3. Показатель р = - 2n, где n - натуральное число.

свойствами:
- область определения - множество R, кроме х=0;

- множество значений - множество R, кроме у=0;
функция нечетная, так как
(-х)-(2n-1) = х-(2n-1);
- функция является убывающей на промежутках х<0 и х>0.
 
График функции y=х-(2n-1) имеет такой же вид, как, например, график функции y=х3 (рис. 4).

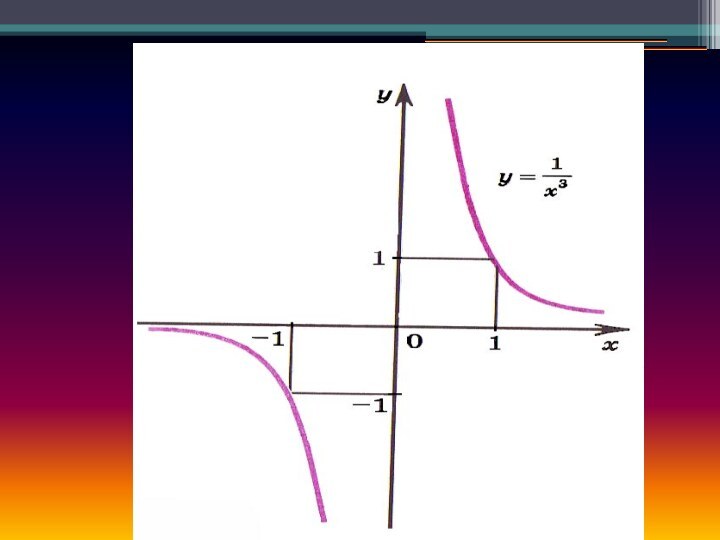
4. Показатель р = - (2n - 1), где n - натуральное число.

В этом случае функция у=хР обладает следующими свойствами:
область

определения - неотрицательные числа х;
множество значений - неотрицательные числа у;
функция является возрастающей на промежутке (x; ∞).

График функции у=хР, где р - положительное нецелое число, имеет такой же вид, как, например, график функции у=хР (при 0<р< 1) или как, например, график функции y=хР (при p>1) (рис.5 a, б)

В этом случае функция у=хР обладает следующими свойствами:
область

определения – положительные числа х>0;
множество значений – положительные числа у >0;
функция является убывающей на промежутке х>0.

Данный случай проиллюстрирован графиками