- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Таңдама тәсіл. Бас жиынтық және таңдама.Таңдаманың репрезентивтігі. Таңдама таралау және оның сипаттамалапы
Содержание
- 2. Дәріс мақсаты: Студенттерді зерттеу объектілері ретінде статистикалық жиынтықпен таныстыру
- 3. Дәріс жоспары: -Бас және таңдамалы жиынтықтар
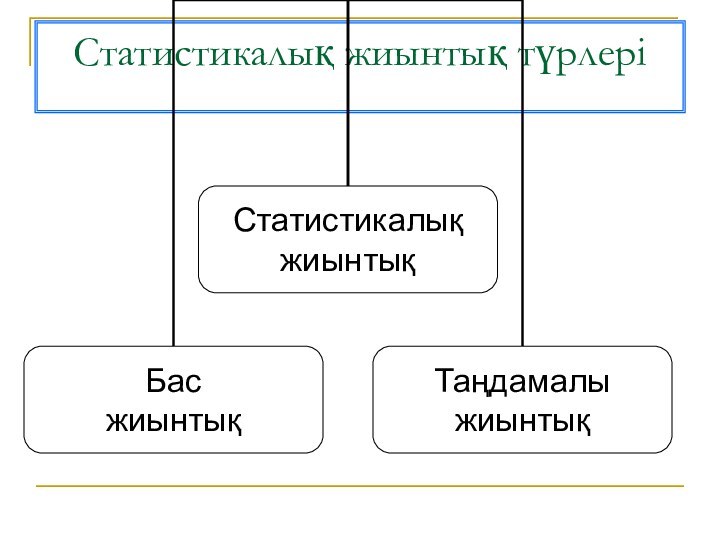
- 4. Статистикалық жиынтық түрлері
- 5. Бір белгілі мерзімде және аймақта,
- 6. Зерттеудің мақсатына байланысты, байқаудың барлық бақылау белгілерінен құралған жиынтықты бас жиынтық дейміз
- 7. Бас жиынтықты сипаттауға арналған және бас
- 8. Таңдама жиынтық репрезентивтік бөлу керек. Репрезентивтік дегеніміз
- 9. Репрезентивтік бөлу үшін қойылатын талаптар -Таңдама
- 10. Зерттеу белгілерден және оның жиіліктерінен құралған қатарды
- 11. Әр бір Х шамасының санына жағдайдың салыстырма жиілігін Х
- 12. Таңдаманың статистикалық таралуын сипаттамасы: нүктелі және интервалдық баға арқылы өткізіледі
- 13. Бір сан арқылы анықталатын бағаны нүктелі баға
- 14. Статистикалық әдістер, сенімділік ықтималдары 1-ге жақын
- 15. Фармация, медицина және биология зерттеулерінде сенімділік
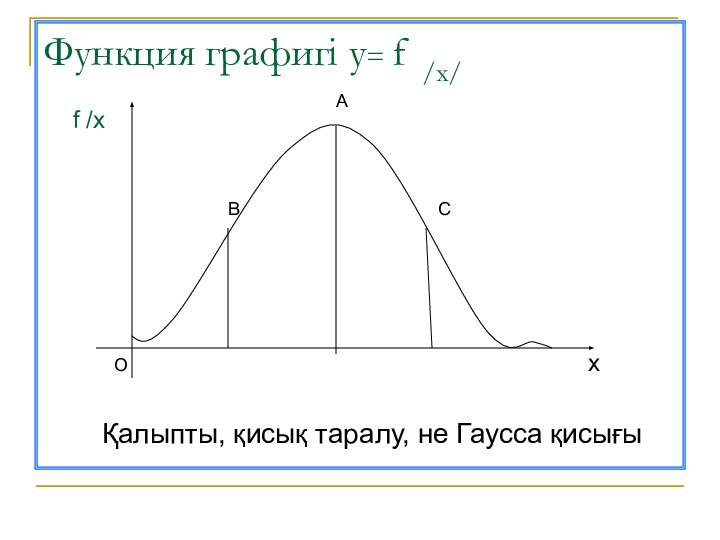
- 16. Үздіксіз кездейсоқ шаманың (х) таралу заңын қалыпты
- 17. Функция графигі у= f /x/f /xАВСОхҚалыпты, қисық таралу, не Гаусса қисығы
- 18. μ =0, және σ =1 параметрлерімен
- 19. 1 Ф(х) =---- е-Х2
- 20. 3 сигма ережесіҚалыпты таралу бойынша:M(+/-)σ=68,26%M(+/-)2σ=95,44%M(+/-)3σ=99,72%,M(+/-)3σ – барлық мүмкіндік сан мәндерінің шегі
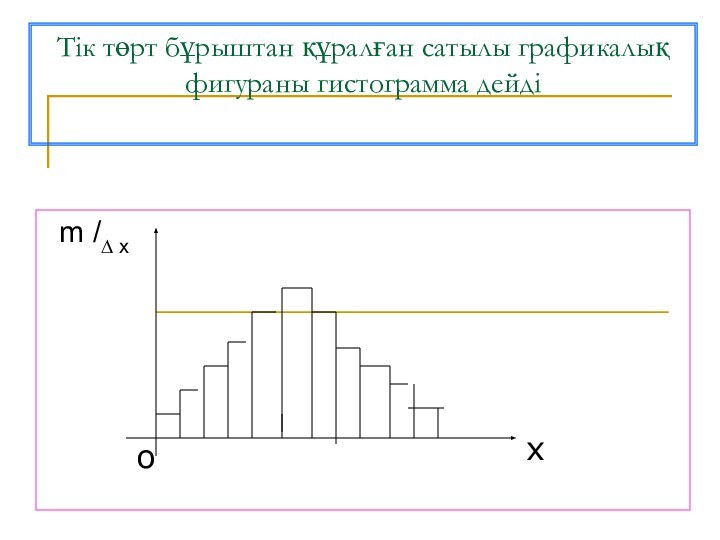
- 21. Статистикалық таралуды графика арқылы бейнелеуде полигонды және гистограмманы қолданады
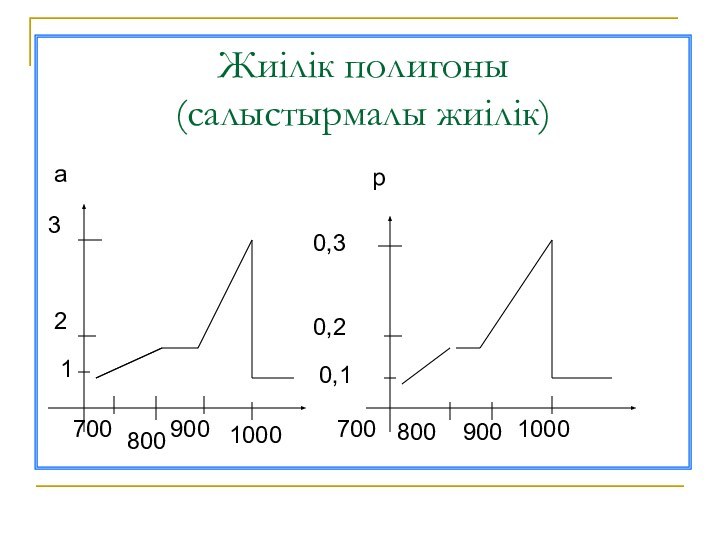
- 22. (Х1 ; m1) не (Х1; Р1) қосатын сызықты жиілік полигоны (салыстырмалы жиілік) дейміз
- 23. Жиілік полигоны (салыстырмалы жиілік)а321800700 9001000р0,30,20,1700 8009001000
- 24. Тік төрт бұрыштан құралған сатылы графикалық фигураны гистограмма дейді m /∆ xxo
- 25. Скачать презентацию
- 26. Похожие презентации
Дәріс мақсаты: Студенттерді зерттеу объектілері ретінде статистикалық жиынтықпен таныстыру