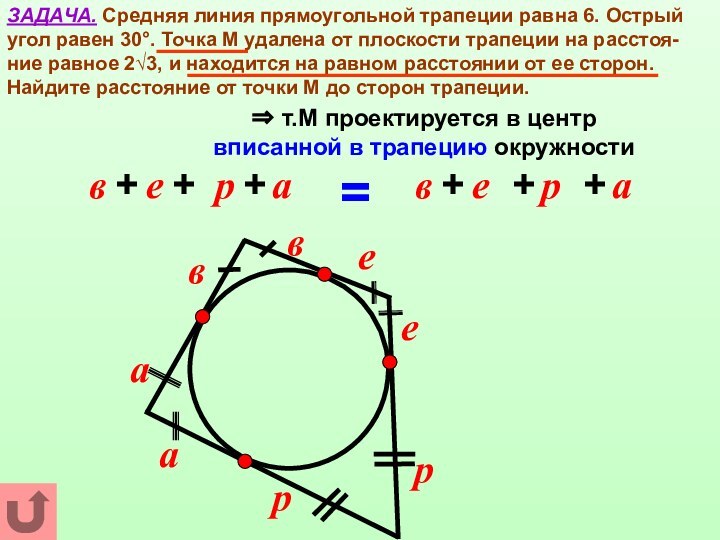
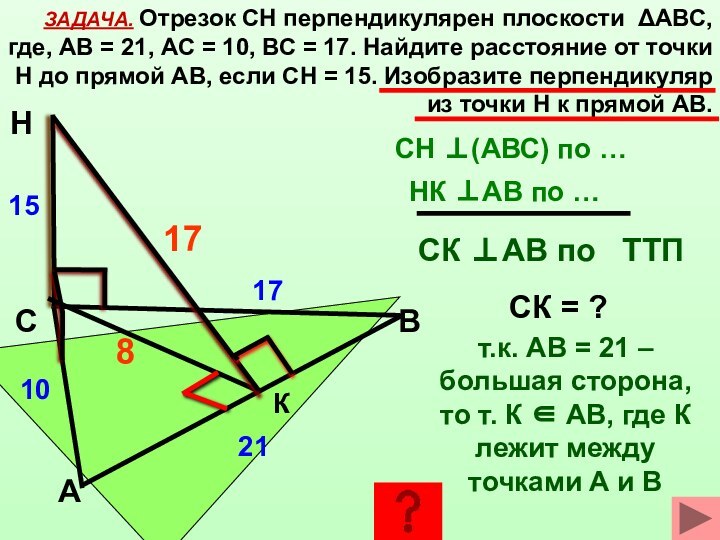
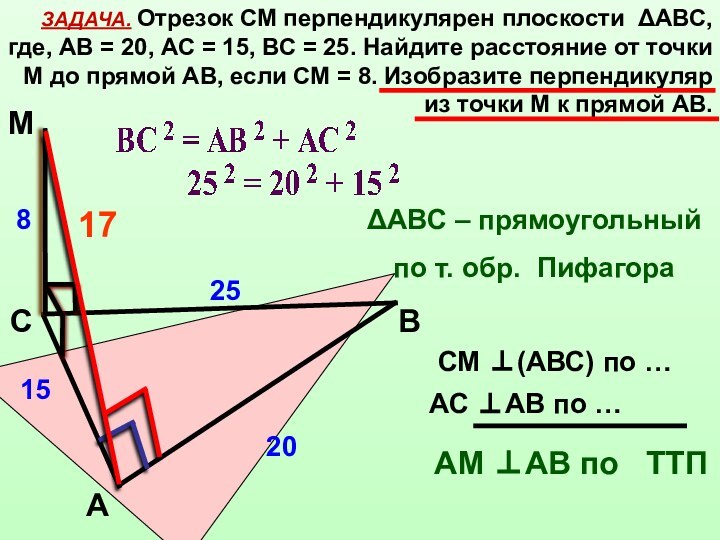
через основание наклонной перпендикулярно к ее проекции на эту
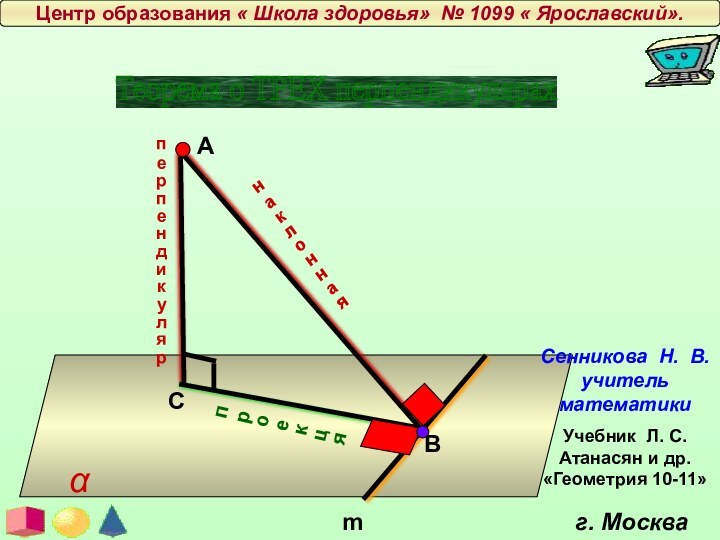
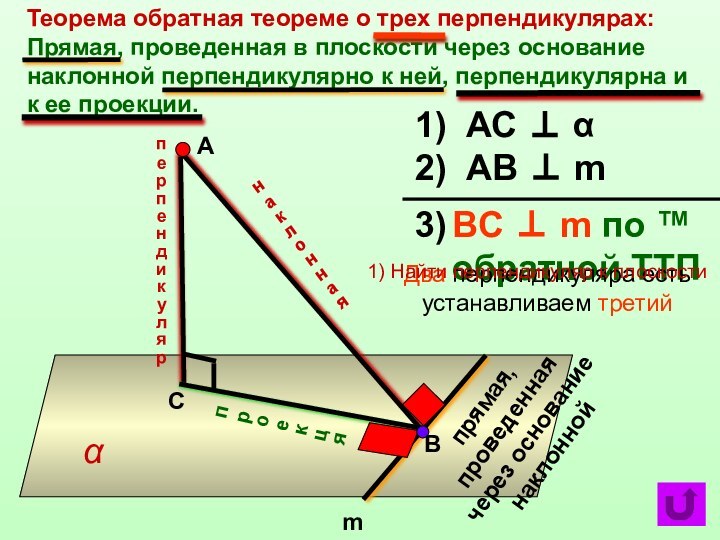
плоскость, перпендикулярна и к самой наклонной.α
А
С
В
п
е
р
п
е
н
д
и
к
у
л
я
р
н
а
к
л
о
н
н
а
я
п
р
о
е
к
ц
И я
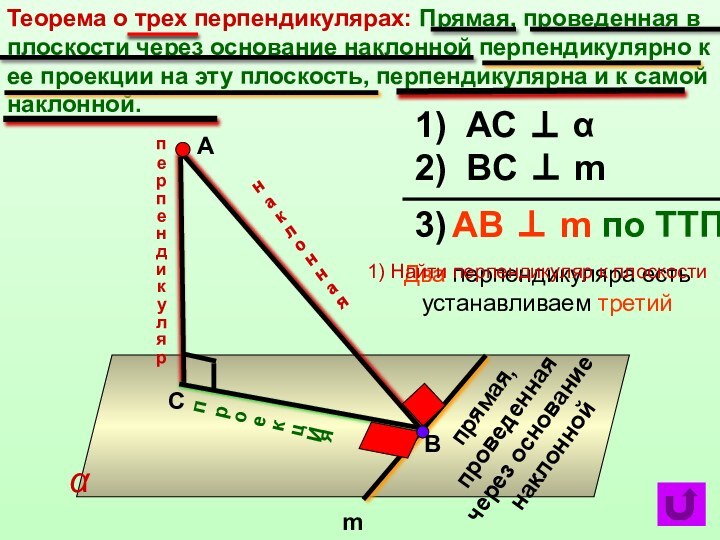
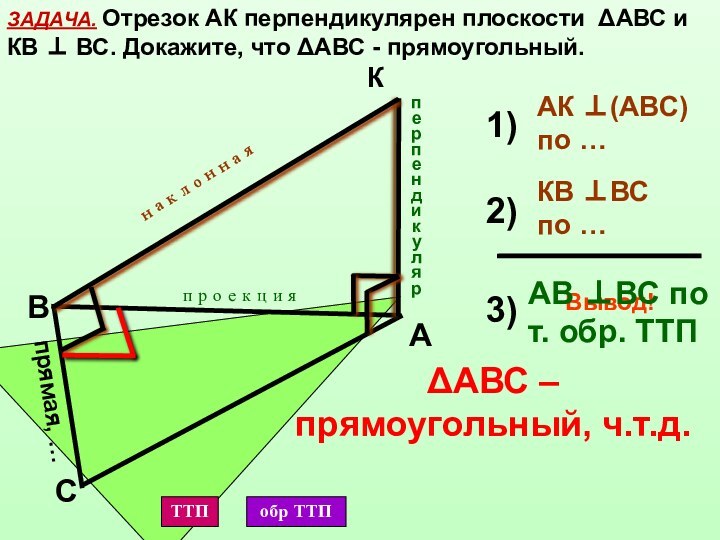
прямая, проведенная через основание наклонной
1)
2)
3)
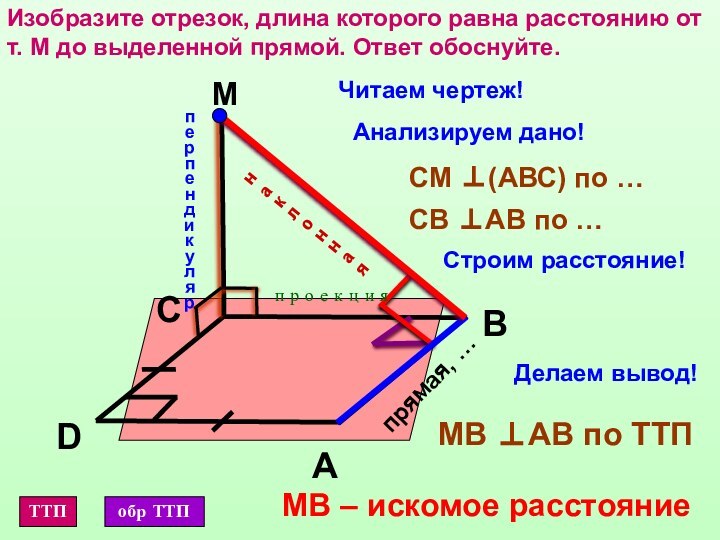
АС ⊥ α
m
BС ⊥ m
АB ⊥ m по ТТП
Два перпендикуляра есть устанавливаем третий
1) Найти перпендикуляр к плоскости