– навечно,
Когда хоть раз в прозрении её увидим свет,
И
теорема Пифагора через столько летДля нас, как для него, бесспорно безупречна…
Шамиссо
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора и способы её доказательства
Содержание
- 2. Cуть истины вся в том, что нам
- 4. Цель:Рассмотреть классические и малоизвестные доказательства теоремы Пифагора
- 5. Пифагор Самосский (570-500 гг. до н.э.)
- 6. Некоторые факты из жизни Пифагора:Родился на о.Самосе
- 7. РАЗЛИЧНЫЕ СПОСОБЫ ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ ПИФАГОРА
- 8. Формулировка теоремы ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.cab
- 9. ДОКАЗАТЕЛЬСТВО, основанное на равновеликости фигур:«Квадрат, построенный
- 10. Алгебраический метод доказательства теоремы:ccccaaaabbbbПусть F- прямоугольный треугольник
- 11. Доказательство теоремы
- 12. Векторное доказательство теоремы:АВС - прямоугольный треугольник,
- 13. Доказательство Гарфилда:ABC-прямоугольный треугольник 1)CD =AВ; ED=АС;
- 14. Пусть катеты прямоугольных ▲-ков d равны a
- 16. ABC-прямоугольный ▲; AJ- высота.Докажем: S1+S2=S31.▲ ABD= ▲
- 17. Области применения теоремы Пифагораархитектурамобильная связьастрономиялитературавычисление длин отрезков некоторых фигур на плоскости
- 18. Знаменитый египетский треугольник3, 4,5-одна из Пифагоровых троек
- 19. Теорема Пифагора- живительный источник красоты, совершенства и творчества для новых поколений!
- 20. Скачать презентацию
- 21. Похожие презентации
Cуть истины вся в том, что нам она – навечно,Когда хоть раз в прозрении её увидим свет,И теорема Пифагора через столько летДля нас, как для него, бесспорно безупречна…
Слайд 2 Cуть истины вся в том, что нам она
– навечно,
теорема Пифагора через столько летДля нас, как для него, бесспорно безупречна…
Шамиссо
Слайд 3 «Геометрия
обладает двумя
великими сокровищами. Первое – это теорема Пифагора…»Теорема Пифагора
красота
простота
значимость
Иоганн Кеплер
Слайд 4
Цель:
Рассмотреть классические и малоизвестные доказательства теоремы Пифагора
Познакомиться
с областями применения теоремы и с фактами истории открытия
теоремы ПифагораСделать выводы о значимости теоремы Пифагора
Слайд 6
Некоторые факты из жизни Пифагора:
Родился на о.Самосе около
570 г. до н.э.
Учился во многих городах мира
у великих учёных- Ферекида, Фалеса, Гермодаманта… В Египте Пифагор попал в персидский плен,где пробыл 12 лет
В Кротоне(Италия) учредил «Пифагорейскую школу»
Слайд 8
Формулировка теоремы Пифагора
В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов.
c
a
b
Слайд 9
ДОКАЗАТЕЛЬСТВО,
основанное на равновеликости фигур:
«Квадрат, построенный на гипотенузе
прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах».
Слайд 10
Алгебраический метод доказательства теоремы:
c
c
c
c
a
a
a
a
b
b
b
b
Пусть F- прямоугольный треугольник со
сторонами a,b и c,а Q- квадрат со стороной с.
SABCD= 4S▲ + SQ=
= 4·1/2 ab +c2 =
= 2 ab + c2
SABCD= (а+b)2 = a2 + 2ab +b2
2 ab + c2 =a2 + 2ab +b2
=> c2 = a 2 +b 2
A
B
D
C
F
F
F
F
F
Q
Слайд 11 Доказательство теоремы Пифагора
через косинус угла:
D
A
C
B
c
a
b
Построим высоту из прямого угла С. По
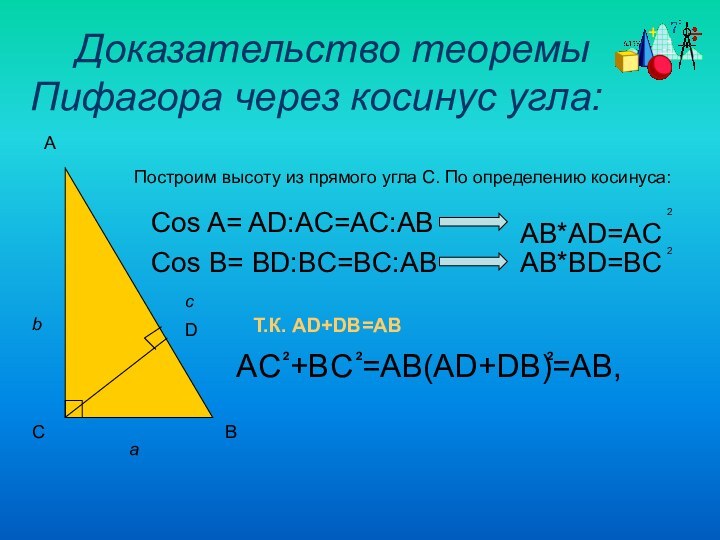
определению косинуса:Cos A= AD:AC=AC:AB
2
AB*AD=AC
Сos B= BD:BC=BC:AB
AB*BD=BC
2
Т.К. AD+DB=AB
AC +BC =AB(AD+DB)=AB,
2 2 2
Слайд 12
Векторное доказательство
теоремы:
АВС - прямоугольный треугольник, построенный на
векторах.
b+c=a
c = a - bc²=a²+b²-2ab
Т.к. a b, то ab=0, c²=a²+b² или c²=a²+b²
Слайд 13
Доказательство Гарфилда:
ABC-прямоугольный треугольник
1)CD =AВ; ED=АС; ЕD
AD
2) SABED=2*AB*AC/2+BC/ 2 3) SABED=(DE+AB)*AD/2.
4) AB*AC+BC /2=(DE+AB)(CD+AC)/2
AB*AC+BC /2= (AC+AB)
/2AB*AC+BC/2= AC/2+AB/2+AB*AC
BC=AB+AC
2
2
2
2
2
2
2
2
2
2
Слайд 14
Пусть катеты прямоугольных ▲-ков d равны a и
b, а гипотенуза – с.
Тогда (a − b)
+(4ab)/2= с, то естьДОКАЗАТЕЛЬСТВО БХАСКАРИ-АЧАРНА:
С
С
С
С
d
d
d
d
2
2
a
a
a
a
b
b
b
b
Слайд 15
ABC-прямоугольный ▲ повернем на 90° так, чтобы он занял
положение A'CB'.▲ A'АВ'В : AA’C=b²/2
SCBB'=a²/2
SA'AB'B=(a²+b²)/2
▲ A'В'А и ▲ A'В'В: DA и DB-общие,
SA'AB'B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2
Сравнивая полученные выражения:
(a²+b²)/2= c²/2 a²+b²=c²
Доказательство Хоукинса:
С
1.
2.
С
Слайд 16
ABC-прямоугольный ▲; AJ- высота.
Докажем: S1+S2=S3
1.▲ ABD= ▲ BFC
(т.к. BF=AB; BC= BD; FBC равен
ABD)2. S ▲ ABD=1/2 S BJLD, т.к. у ▲ ABD и BJLD общее основание BD и общая высота LD.
S ▲ FBC=1/2 S ABFH (BF-общ.основание, AB-общая высота).
Т.К. S ▲ ABD=S ▲ FBC, S BJLD=S ABFH.
▲ BCK=▲ ACE, S JCEL=S ACKG.
S ABFH+S ACKG=S BJLD+ S JCEL=S BCED.
.
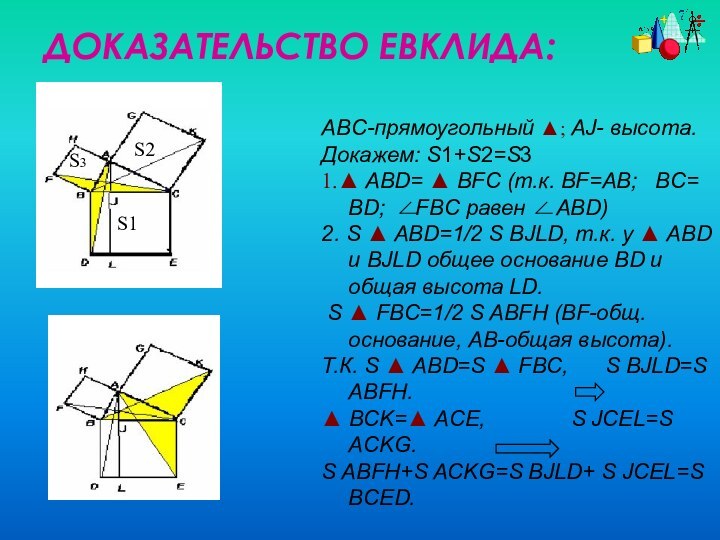
ДОКАЗАТЕЛЬСТВО ЕВКЛИДА:
S3
S2
S1
Слайд 17
Области применения теоремы Пифагора
архитектура
мобильная связь
астрономия
литература
вычисление длин отрезков
некоторых
фигур на плоскости
Слайд 19 Теорема Пифагора- живительный источник красоты, совершенства и творчества
