Слайд 3
Цель: Выяснить какие системы счисления существуют, какое применение
находят различные системы счисления в практической деятельности.
Задачи:
Изучить литературу
по теме «Системы счисления»;
узнать, что такое «Система счисления», какие бывают системы счисления;
выяснить, как используются элементы различных систем счисления в наше время;
выяснить, является ли десятичная система счисления единственной, широко используемой системой счисления;
выяснить, чем может быть интересна тема «Системы счисления» ученикам 5 класса;
представить результаты работы в виде реферата и презентации.
Слайд 4
Древние системы счисления
В обычной жизни мы привыкли пользоваться
десятичной системой счисления. Эта система счисления является позиционной. В
записи чисел в десятичной системе счисления значение каждой цифры
определяется не только ею самой, но и местом (позицией), на котором она стоит.
Кроме привычной нам десятичной системы счисления существуют и другие системы счисления, элементы которых используются и в наши дни, к ним относятся:
Слайд 5
Унарная (единичная) - любое число образуется путем повторения
одного знака, символизирующего единицу. Самая первая историческая система счисления
была единичной или унарной (вспомните зарубки на дереве). Палочка, зарубка была тем самым почти единственным символом, с помощью которого записывались все числа.
Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища).
Слайд 6
Древнекитайская
Данная система счета была основана на использовании счетной
доски, на которой небольшие по размерам (чаще около 15
см) палочки помещались в соответствующие позиции, чтобы символизировать определенные разряды чисел. Палочки изготавливались из бамбука, а в 9 в. из литого железа. Носились палочки по 271 штуки в пачке. Действия сложения, вычитания, умножения и деления осуществлялись посредством перемещения палочек.
Преимущество такого способа подсчета состояло в том, что в любой момент палочки могли быть удалены со счетной доски.
Слайд 7
Алфавитные системы счисления (например, славянский цифровой алфавит)
Слайд 8
Римская нумерация
Римляне вместо цифр использовали всего 7 букв:
I - 1, V - 5, X - 10,
L - 50, C - 100, D – 500, М – 1000. А горизонтальная линия над цифрой увеличивала её значение в 1000 раз.
Слайд 9
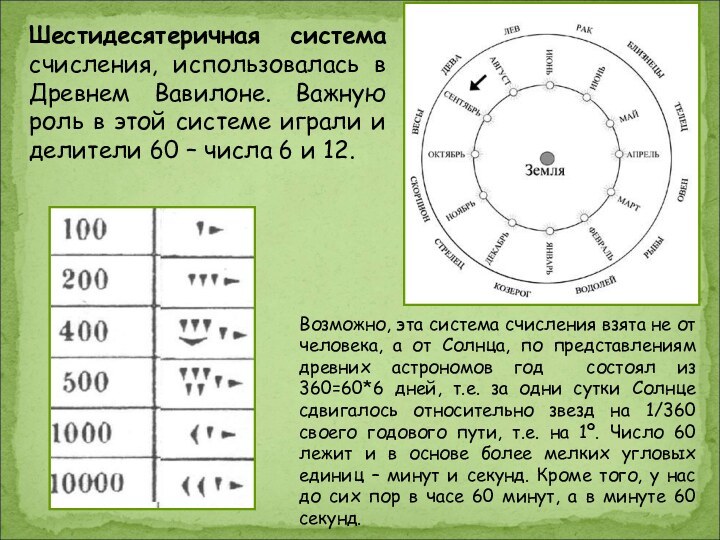
Шестидесятеричная система счисления, использовалась в Древнем Вавилоне. Важную
роль в этой системе играли и делители 60 –
числа 6 и 12.
Возможно, эта система счисления взята не от человека, а от Солнца, по представлениям древних астрономов год состоял из 360=60*6 дней, т.е. за одни сутки Солнце сдвигалось относительно звезд на 1/360 своего годового пути, т.е. на 1º. Число 60 лежит и в основе более мелких угловых единиц – минут и секунд. Кроме того, у нас до сих пор в часе 60 минут, а в минуте 60 секунд.
Слайд 10
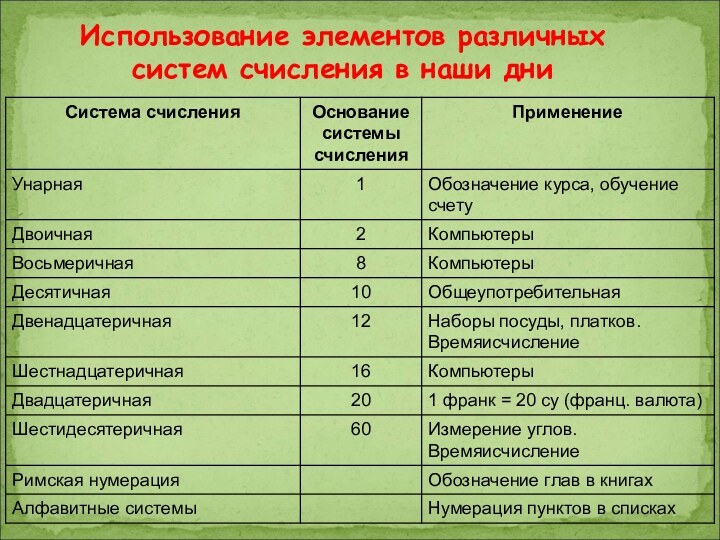
Использование элементов различных систем счисления в наши дни
Слайд 11
Системы счисления анатомического происхождения
Слайд 12
Унарная (единичная) система счисления
=
Слайд 13
Пятеричная система счисления
У ряда африканских племен была
распространена пятеричная система счисления. Долгое время пользовались пятеричной системой
счисления и в Китае. Очевидна связь этой системы счисления со строением человеческой руки.
Слайд 14
Древнеегипетская десятичная непозиционная система
Для обозначения ключевых чисел
1, 10, 100 и т.д. использовались специальные значки –
иероглифы. Все остальные числа составлялись из этих ключевых при помощи операции сложения.
Система счисления Древнего Египта является десятичной, но непозиционной.
Слайд 15
Двенадцатеричная система счисления
Вместо десятков применяли при счете дюжины,
т.е. группы из двенадцати предметов. Происхождение её тоже связано
со счётом на пальцах.
Элементы двенадцатеричной системы счисления сохранилась в Англии в системе мер (1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам). Нередко и мы сталкиваемся в быту с двенадцатеричной системой счисления: чайные и столовые сервизы на 12 персон, комплект носовых платков – 12 штук. В году 12 месяцев, сутки составляют 24 часа=12*2.
Слайд 16
Двадцатеричная система счисления
У ацтеков и майя была принята
двадцатеричная система счисления. Также двадцатеричная система счисления была принята
и у кельтов, населявших Западную Европу начиная со второго тысячелетия до нашей эры.
Основу для счёта в этой системе счисления составляли пальцы рук и ног. Некоторые следы двадцатеричной системы счисления кельтов сохранилось во французской денежной системе: основная денежная единица, франк, делится на 20 (1 франк = 20 су).
Слайд 17
Современная десятичная система счисления
Язык чисел, как и
любой другой, имеет свой алфавит. В том языке чисел,
которым мы обычно пользуемся, алфавитом служат десять цифр – от 0 до 9. Это десятичная система счисления. Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Десять пальцев рук – вот аппарат для счета, которым человек пользуется с доисторических времен. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 – углов нет, 2 – два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.
В записи десятичных чисел используются 10 цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Слайд 18
Системы счисления с основаниями 2, 8, 16
Десятичная система
счисления не единственно возможная. За основание системы счисления можно
взять любое число. Например, в информатике пользуются двоичной системой счисления.
Использование двоичной системы счисления в качестве внутренней системы представления информации вызвано конструктивными особенностями элементов вычислительных машин, При создании компьютеров используется возможность осуществлять автоматическую обработку информации, реализуя только два состояния элементов компьютера «намагничено» и «не намагничено».
Слайд 19
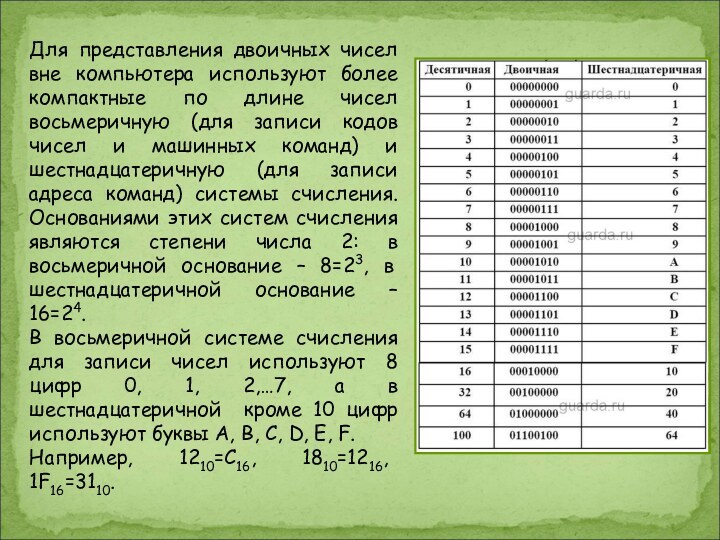
Для представления двоичных чисел вне компьютера используют более
компактные по длине чисел восьмеричную (для записи кодов чисел
и машинных команд) и шестнадцатеричную (для записи адреса команд) системы счисления. Основаниями этих систем счисления являются степени числа 2: в восьмеричной основание – 8=23, в шестнадцатеричной основание – 16=24.
В восьмеричной системе счисления для записи чисел используют 8 цифр 0, 1, 2,…7, а в шестнадцатеричной кроме 10 цифр используют буквы A, B, C, D, E, F.
Например, 1210=С16, 1810=1216, 1F16=3110.
Слайд 20
Теперь мы можем ответить на вопрос «может ли
7+5=14?»
Если считать в десятичной системе счисления, то ответ, конечно,
будет отрицательным, а если предположить, что эти числа записаны в восьмеричной системе счисления, то – утвердительным.
7+5=148
Слайд 21
Математические игры и фокусы
Алгоритм перевода из двоичной
системы в десятичную прослеживается в методе дихотомии – методе
половинного деления. Этот метод широко используется в математике, например, для решения сложных уравнений с помощью вычислительной техники. На принципе дихотомии основана олимпийская система выявления чемпиона. А школьники, увлеченные математикой, используют этот метод в математических играх. Многим известна игра «Угадай число». Вы загадываете число, а ваш приятель пытается его угадать. Потом наоборот. Тот, кто угадал число за меньшее число вопросов, тот выиграл. Используя метод дихотомии и верно поставленные вопросы, число в пределах 64 можно угадать не более, чем за 6 вопросов, а число, не превосходящее 128 – за 7 вопросов.
Слайд 22
Существует другая игра – фокус, в которой для
угадывания числа в пределах 64 потребуется ровно 3 вопроса:
Какого
цвета число в 1 таблице?
Какого цвета число во 2 таблице?
Какого цвета число в 3 таблице?
Для этой игры понадобятся 3 цветных таблицы с числами и шпаргалка.
Получив ответ на просьбу загадать число и ответы на 3 вопроса, ведущий с помощью шпаргалки легко угадывает число. Если вы ответили на вопросы, скажем так: «Синий, зеленый, красный», я складываю три числа 0, 12, 16, стоящих на пересечении столбцов и строк, соответствующих названным цветам в соответствующих таблицах. Получаем число 28.
Слайд 23
Секрет этого фокуса.
С раннего детства мы привыкли

записывать числа в десятичной системе счисления. Например, последовательность цифр
1987 мы расшифровываем как 1·103 + 9·102 + 8·1О1 + 7·10°. Счет ведется десятками, десять единиц одного разряда является единицей следующего разряда. Если же за основание системы счисления взять число 4, а не 10, понадобится всего 4 цифры: 0,1, 2 и 3. Заменим для наглядности цифры буквами. Можно, например, использовать буквы: С — для нуля, К – для 1, Ч — для 2 и З — для 3. Число 28 запишется в четверичной системе счисления как 1·42+3·41+0·4°=1304. А в буквенной записи оно запишется, как КЗС.
Если прочесть эту запись «справа- налево», получится «синий — зеленый — красный». Это сочетание цветов мы и называли, когда, задумав число 28, сообщали его цвета в таблицах А, Б, В.
Взглянем еще раз на таблицы. В таблице А цвета чисел периодически чередуются через четыре. Таким образом, у синих чисел в четверичной записи стоит на конце число 0, у красных —1, у черных — 2, у зеленых – 3. Цвета чисел в таблице Б точно таким способом определяют вторую цифру в четверичной записи числа, а в таблице В — третью цифру. То же самое говорит и «шпаргалка», с помощью которой мы определяли число по его цветам в таблицах.
Слайд 24
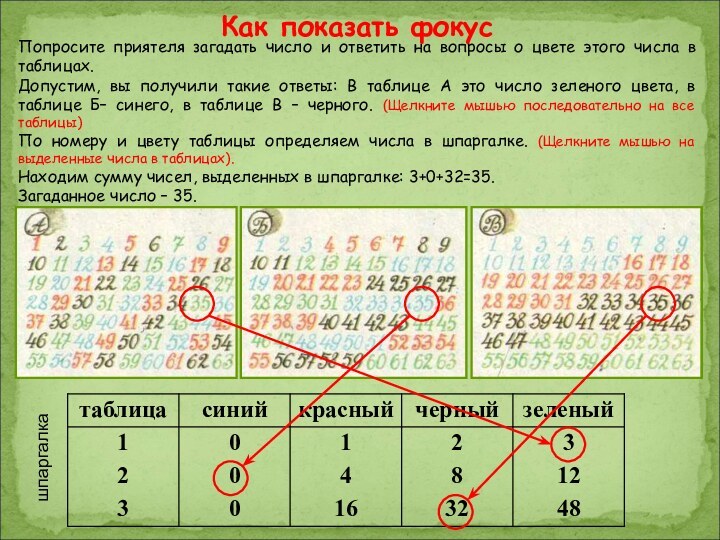
Попросите приятеля загадать число и ответить на вопросы
о цвете этого числа в таблицах.
Допустим, вы получили такие
ответы: В таблице А это число зеленого цвета, в таблице Б– синего, в таблице В – черного. (Щелкните мышью последовательно на все таблицы)
По номеру и цвету таблицы определяем числа в шпаргалке. (Щелкните мышью на выделенные числа в таблицах).
Находим сумму чисел, выделенных в шпаргалке: 3+0+32=35.
Загаданное число – 35.
шпаргалка
Как показать фокус
Слайд 25
Такой же принцип, но с опорой на двоичную
систему счисления имеет и другой математический фокус – «Угадай
фигуру».
В этом фокусе ведущий предлагает загадать фигуру и сообщить, в каких столбцах таблицы она записана. С помощью шпаргалки ведущий угадывает задуманную фигуру.
Слайд 26
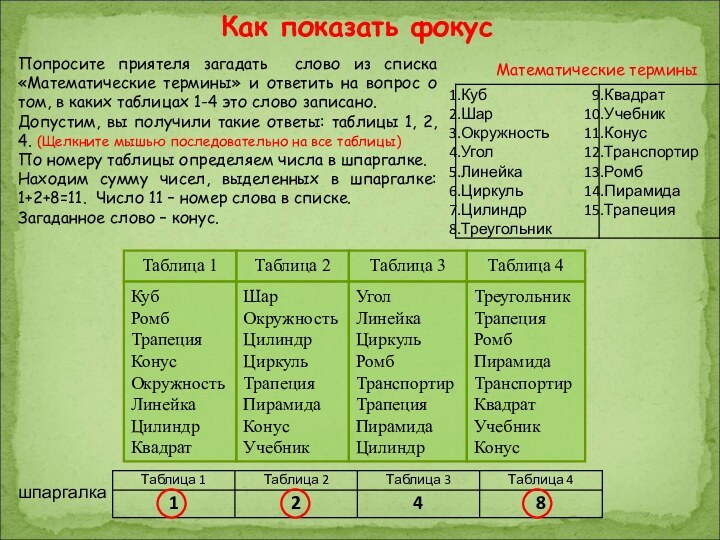
Попросите приятеля загадать слово из списка «Математические термины»
и ответить на вопрос о том, в каких таблицах
1-4 это слово записано.
Допустим, вы получили такие ответы: таблицы 1, 2, 4. (Щелкните мышью последовательно на все таблицы)
По номеру таблицы определяем числа в шпаргалке.
Находим сумму чисел, выделенных в шпаргалке: 1+2+8=11. Число 11 – номер слова в списке.
Загаданное слово – конус.
Как показать фокус
шпаргалка
Математические термины
Слайд 27
Вывод
Изучив литературу по теме «Системы счисления», я узнал,
что в древности люди пользовались различными системами счисления, позиционными
и непозиционными. Многие системы счисления имеют анатомическое происхождение. Элементы некоторых систем счисления имеют практическое применение в наши дни. Общеупотребительной системой счисления стала десятичная система счисления. Но и другие системы счисления имеют практическое применение, например системы счисления с основаниями 2, 8, 16. Правила, связанные с системами счисления помогают в практической деятельности человека, например, метод дихотомии позволяет определить количество игр на Олимпиаде. А ученикам 6 класса системы счисления помогают показать математику с другой стороны – математика может быть еще и средством развлечения.