Слайд 2
Цель работы:
на основе полученных знаний, о свойствах
и правилах построения многогранников, создать совершенно новый многогранник.
Объект
исследования:
многогранник, как модель различных тел.
Предмет исследования:
процесс использования многогранников в разных сферах жизни и науках.
Слайд 3
Гипотеза: мы считаем, что многогранник являясь моделью различных
тел используется в разных сферах жизни человека и науках.
Задачи:
-
Дать понятие правильных многогранников ( на основе определения многогранников)
- Рассмотреть свойства правильных многогранников.
- Познакомить с историческими фактами, связанными с теорией правильных многогранников.
- Научиться моделировать различные геометрические тела
Слайд 4
Математика владеет не только истиной, но и высшей
красотой - красотой отточенной и строгой, возвышенно чистой и
стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел
Слайд 5
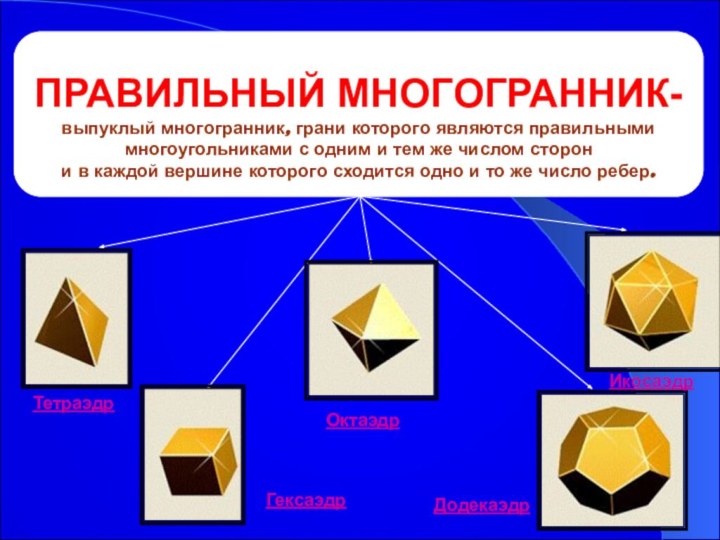
ПРАВИЛЬНЫЙ МНОГОГРАННИК-
выпуклый многогранник, грани которого являются правильными
многоугольниками
с одним и тем же числом сторон
и в
каждой вершине которого сходится одно и то же число ребер.
Гексаэдр
Тетраэдр
Октаэдр
Додекаэдр
Икосаэдр
Слайд 6
«эдра» - грань
«тетра» - 4
«гекса» -
6
«окта» - 8
«икоса» - 20
«додека» -
12
Слайд 7
Правильными многогранниками
называют выпуклые многогранники, все грани
и все углы которых равны, причем грани -
правильные многоугольники.
В каждой вершине правильного многогранника сходится одно и то же число рёбер .
Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многоугольника равны.
Правильные многогранники - трехмерный аналог плоских правильных многоугольников.
Слайд 8
Тетраэдр не имеет центра симметрии, но у него
есть 3 оси симметрии и 6 плоскостей симметрии.
Слайд 9
Куб имеет один центр симметрии, 9 осей симметриии
9 плоскостей симметрии.
Слайд 10
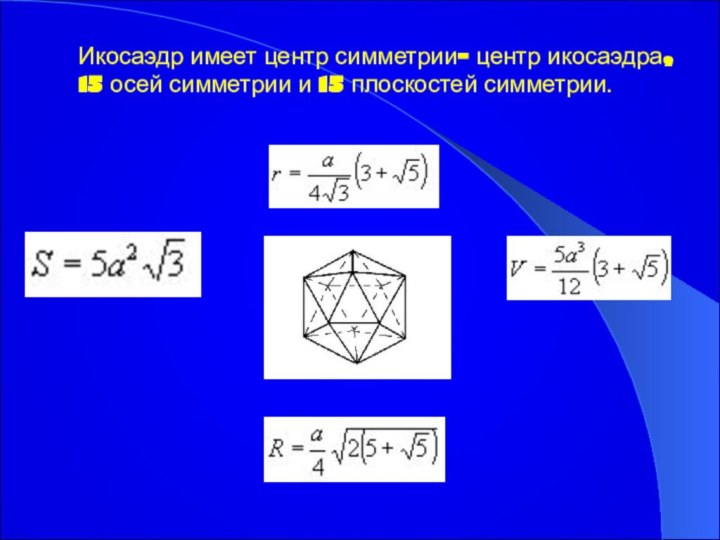
Икосаэдр имеет центр симметрии- центр икосаэдра, 15 осей
симметрии и 15 плоскостей симметрии.
Слайд 11
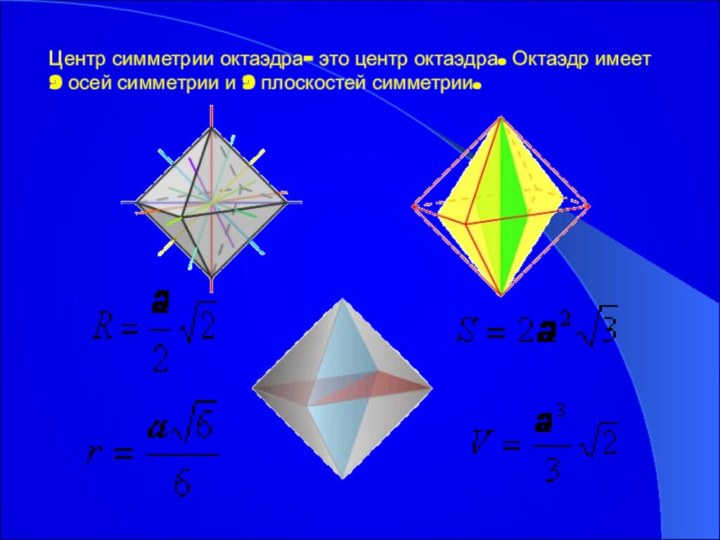
Центр симметрии октаэдра- это центр октаэдра. Октаэдр имеет
9 осей симметрии и 9 плоскостей симметрии.
Слайд 12
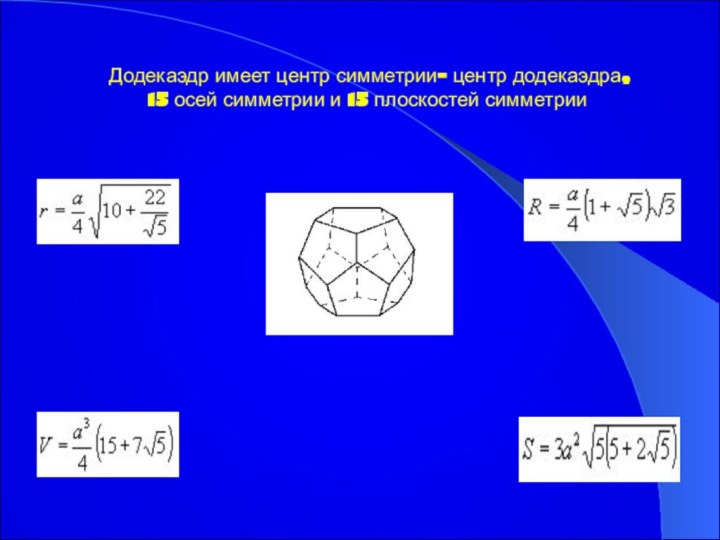
Додекаэдр имеет центр симметрии- центр додекаэдра,
15 осей
симметрии и 15 плоскостей симметрии
Слайд 14
Число =В-Р+Г называется эйлеровой характеристикой многогранника. Согласно теореме
Эйлера, для выпуклого многогранника эта характеристика равна 2. То
,что эйлерова характеристика равна 2 для некоторых знакомых нам многогранников, видно из таблицы.
Слайд 15
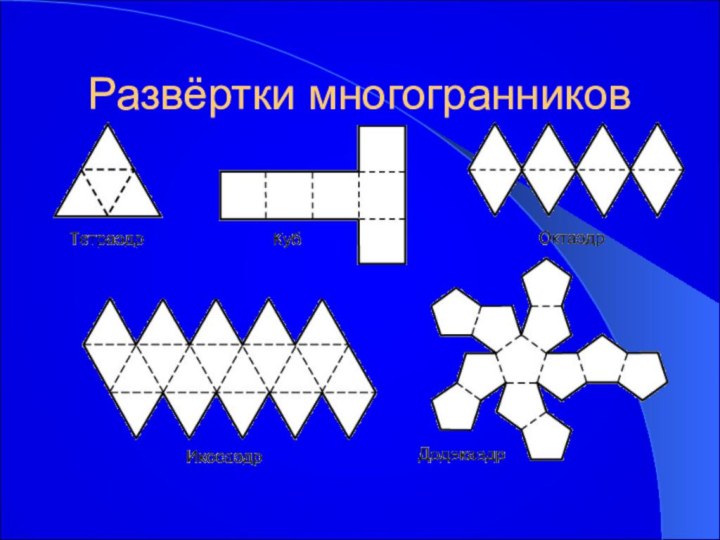
Развёртки многогранников
тетраэдр
куб
октаэдр
икосаэдр
додекаэдр
Слайд 16
Тетраэдр
Икосаэдр
Гексаэдр
Додекаэдр
Октаэдр
Слайд 17
огонь
тетраэдр
вода
икосаэдр
воздух
октаэдр
земля
гексаэдр
вселенная
додекаэдр
стихии
Слайд 18
Выводы:
Многогранник называется правильным, если:
Он выпуклый;
Все его грани равные
правильные многоугольники;
В каждой вершине сходится одно число граней;
Все его
двугранные углы равны.
Слайд 19
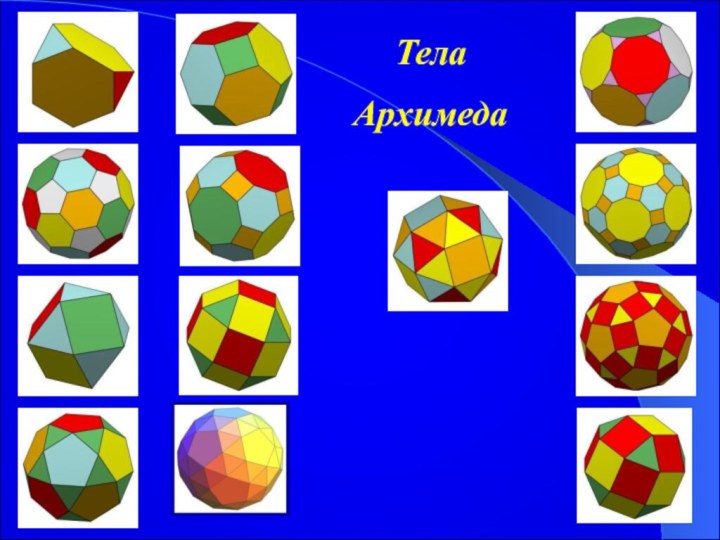
Тела Архимеда
Архимедовыми телами называются полуправильные однородные выпуклые многогранники,
то есть выпуклые многогранники, все многогранные углы которых равны,
а грани - правильные многоугольники нескольких типов.
Слайд 21
Тела
Кеплера - Пуансо
Среди невыпуклых однородных многогранников существуют
аналоги платоновых тел - четыре правильных невыпуклых однородных многогранника
или тела Кеплера - Пуансо.
Как следует из их названия, тела Кеплера-Пуансо - это невыпуклые однородные многогранники, все грани которых - одинаковые правильные многоугольники, и все многогранные углы которых равны. Грани при этом могут быть как выпуклыми, так и невыпуклыми.
Слайд 22
Большой звездчатый
додекаэдр
Большой икосаэдр
Малый звездчатый
додекаэдр
Большой додекаэдр
Слайд 23
Правильных многогранников вызывающе мало, но этот весьма скромный
по численности отряд сумел пробраться в самые глубины различных
наук.
Л. Кэррол
Слайд 24
Химия.
Строение атома
поваренной соли
Кристалл
поваренной соли
Строение
атома
метана
Слайд 25
Вирус полиомиелита имеет форму додекаэдра.
Слайд 26
Икосаэдр оказался в центре внимания биологов в их
мнениях относительно формы вирусов.
Слайд 27
Капсида вируса с икосаэдрической симметрией.
Слайд 28
Феодария
Вирусы
Структура ДНК генетического кода жизни – представляет
собой четырехмерную развертку (по оси времени) вращающегося додекаэдра.
Слайд 29
Многогранники в природе.
Правильные многогранники – самые выгодные фигуры.
И природа этим широко пользуется. Подтверждением тому служит форма
некоторых кристаллов.
Кристалл сульфата меди II
Кристалл алюмокалиевых
квасцов
Кристалл сульфата никеля II
Слайд 30
Кристаллы
Шестой элемент периодической системы С(углерод) характеризуется структурой октаэдра.
Кристаллы октаэдра обычно имеют форму октаэдра.
Рубин
Алмаз
Слайд 31
Кристаллы в форме призм.
Рубин
Горный хрусталь
Слайд 32
В эпоху Возрождения большой интерес к формам правильных
многогранников проявили скульпторы. Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер
(1471- 1528) , в известной гравюре
''Меланхолия '‘ на переднем плане изобразил додекаэдр.
Слайд 34
Математика, в частности геометрия, представляет собой могущественный инструмент
познания природы, создания техники и преобразования мира.
Слайд 38
«Мой дом построен по законам самой строгой архитектуры.
Сам Евклид мог бы поучиться, познавая мою геометрию»
Пчелы
строили шестиугольные соты задолго до появления человека.
Слайд 40
Проект «Звездное небо».
Целью проекта было создание совершенно нового
многогранника шарообразной формы. За основу были взяты плоские фигуры
звезды и ромба.
Количество звезд-12,
количество ромбов- 30.
Слайд 42
Целью проекта было создание совершенно нового полуправильного многогранника
звездчатой формы.
Количество пирамид в мини-звезде 12
шт. , в проекте «Звезда Элан» использовано 12 мини-звезд или 144 пятигранные выпукло-вогнутые пирамидки.
Проект «Звезда Элан».
Слайд 43
«Звезда Элан»
Модель большого икосаэдра-12 шт.
Развертка Элан