Слайд 2
Движение планет Солнечной системы удобно рассматривать в СО,
связанной с Солнцем (в гелиоцентрической СО)
Начало этой СО совпадает
с центром Солнца, а координатные оси направлены на удаленные звезды. В этой СО наша планета движется вокруг Солнца. Кроме Земли, вокруг Солнца движется еще ряд планет : Меркурий, Венера, Марс, Сатурн, Юпитер, Уран и Нептун.
Ближайшие к Земле планеты – Меркурий, Венера и Марс-называют планетами земной группы.
Слайд 4
Траектории движения планет Солнечной системы представляют собой эллипсы.
Однако при приблизительных расчетах можно считать, что все планеты
движутся равномерно по окружностям, центром которых является центр Солнца.
Гелиоцентрическую СО с высокой степенью точности можно считать инерциальной. Поэтому в ней применимы законы Ньютона.
Слайд 5
Вокруг некоторых планет Солнечной системы движутся их естественные
спутники (подобно тому, как сами планеты движутся вокруг Солнца).
Самым
известным примером такого спутника является Луна – это естественный спутник Земли.
Движение спутника удобно рассматривать в СО, начало которой совпадает с центром планеты, а оси направлены на удаленные звезды.
Слайд 6
Луна в такой СО, начало которой совпадает с
центром Земли, движется по эллиптической орбите. Можно считать, что
в этой СО Луна движется равномерно по окружности, в центре которой расположена Земля. Поэтому, движение Луны в СО, связанной с Землей, подобно движению любой из планет Солнечной системы в гелиоцентрической СО. Эту СО для решения рассмотренных здесь задач также можно считать инерциальной.
Слайд 7
Рассмотрим несколько задач.
Задача №1. Определите модуль скорости движения
Луны относительно Земли, а также период Т ее обращения
вокруг Земли.
Решение:
1. Земля, Луна – материальные точки. Луна движется равномерно по окружности радиусом Rл=60Rз, в центе которой находится Земля.
2. ИСО свяжем с Землей и удаленными звездами. За положительное направление оси Х выберем направление от Луны к Земле.
Слайд 8
3. Изображаем силу на рисунке, кот действует на
Луну и силу гравитационного притяжения со стороны Земли. В
учебнике стр.116 рисунок 80.
4. Проекция силы F на ось Х положительна: Fх=F
5. Пишем второй з-н Ньютона в проекции на ось Х для Луны имеет вид F=Мл*а, где Мл- масса Луны, а- проекция на ось Х центростремительного ускорения Луны.
6.Модуль силы равен:F=G* Mл*Mз/R^2
Mз- масса Земли, Mл – масса Луны, R- расстояние от Земли до Луны.
Слайд 11
Проведем анализ полученного ответа. Из (3) и (4)
мы видим, что ни модуль скорости v, ни период
обращения Луны Т не зависят от ее массы. Модуль скорости Луны и период зависят только от гравитационной постоянной, массы Земли и радиуса орбиты.
Значит, если бы вместо Луны по ее орбите под действием гравитационного притяжения Земли двигался др объект, то модуль его скорости и период его обращения были бы такими же, как у Луны.
Слайд 12
При движении любого объекта по окружности радиусом ?
вокруг Земли под действием силы гравитационного притяжения со стороны
Земли модуль скорости этого объекта и период его обращения равны:
v=√(?∗?з)/?,
Т=2π√(?^3/(?∗?з))
Слайд 13
Мы видим, что чем больше радиус окружности ,
по которой движется тело вокруг Земли, тем меньше модуль
его скорости. Период обращения с увеличением расстояния до центра земли увеличивается.
Слайд 16
Задача 2.
Известно, что модуль скорости движения Земли вокруг
Солнца v=30 км/с, а период ее обращения Т= 1
год. Оцените среднее расстояние от Земли до Солнца.
Слайд 18
Задача№3. Зная, что среднее расстояние от Земли до
Солнца равно 1а.е., а модуль скорости движения Земли по
орбите
v=30 км/с, оцените массу Солнца.
Слайд 20
Рассмотрим движение брошенного с высокой горы камня. Пусть
камень брошен параллельно поверхности Земли. Под действием силы тяжести
он пишет кривую траекторию и упадет на Землю. Чем больше будет начальная скорость камня, тем дальше он упадет от места броска. Если бы не было сопротивления воздуха, то можно было бы бросить камень с такой скоростью, что он никогда бы не достиг поверхности Земли. Тогда камень двигался бы вокруг Земли подобно Луне, став спутником нашей планеты.
Слайд 21
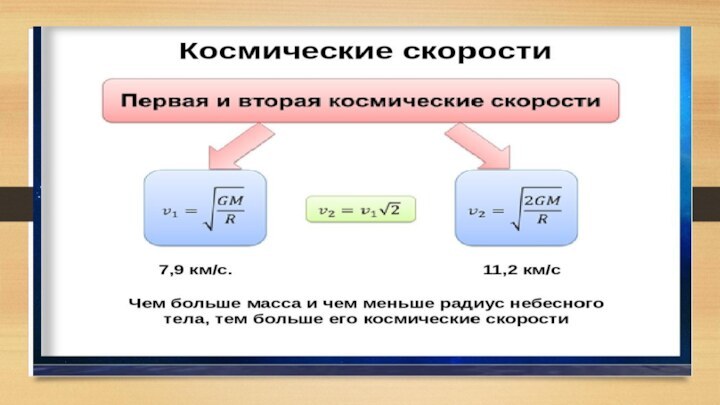
Было установлено, что существует минимальная скорость, которую необходимо
сообщить любому брошенному с поверхности Земли телу, чтобы оно
стало двигаться по орбите вокруг Земли. Эта скорость получила специальное название первая космическая скорость и обозначение: v1.
Слайд 22
Первая космическая скорость для Земли – модуль минимальной
скорости, которую надо сообщить телу, чтобы оно двигалось вокруг
Земли по круговой орбите вблизи ее поверхности только под действием силы гравитационного притяжения Земли.
Слайд 29
1. Во сколько раз первая космическая скорость для
Земли больше, чем для Марса? Радиус планеты Марс составляет
0,53 радиуса Земли, а его масса — 0,11 массы Земли
Слайд 31
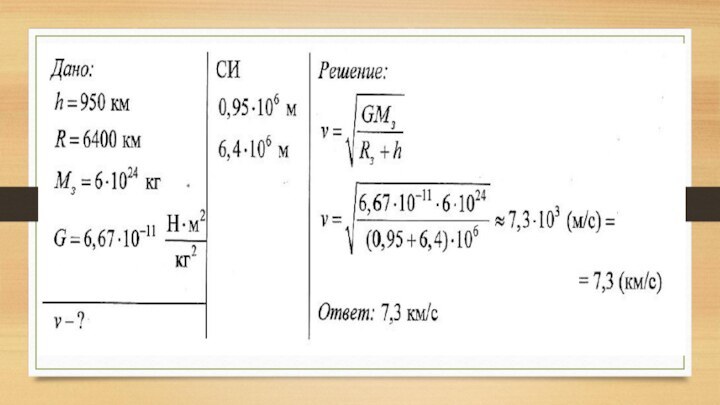
2. Первый искусственный спутник Земли, запущенный в СССР
4 октября 1957 года, двигался на высоте 950 км
над поверхностью Земли. Вычислите скорость этого спутника.
Слайд 33
3. Скорость обращения Земли вокруг Солнца 30 км/с,
радиус земной орбиты 1,5•10^11 м. По этим данным определите
массу Солнца.
Слайд 35
4.Вычислить первую космическую скорость для Луны, принимая радиус
Луны 1700 км, а ускорение свободного падения тел на
Луне — 1,6 м/с2.
Слайд 37
5.Какую скорость должен иметь искусственный спутник, чтобы обращаться
по круговой орбите на высоте 900 км над поверхностью
Земли? Каков период его обращения?
Слайд 39
6. На какой высоте над поверхностью Земли был
запущен искусственный спутник, если он движется со скоростью 7,1
км/с?
Слайд 41
7. чему равна первая космическая скорость на планете
сатурн. Масса 5,69*10²⁶кг,средний радиус сатурна 6,04*10⁷м?
Слайд 43
8. Вычислите ускорение свободного падения и первую космическую
скорость у поверхности Луны.
Слайд 45
9. Планета Марс имеет два спутника — Фобос
и Деймос. Первый находится на расстоянии 9500 км от
центра Марса, второй — на расстоянии 24 000 км. Определите периоды обращения этих спутников вокруг Марса.