Слайд 2
Правила игры:
На игровом поле представлено 15 вопросов. По
жеребьёвке или по договорённости определяется команда, которая первой начинает
игру.
Чтобы перейти к вопросу, необходимо нажать на выбранную цифру. При переходе появляется текст вопроса, на который команда должна ответить за установленный учителем промежуток времени.
При следующем нажатии в левом нижнем углу появляется изображение кнопки «Ответ». Оно предупреждает, что команде необходимо отвечать, а также позволяет избежать случайного перехода на слайд с ответом.
Если команда не смогла ответить на вопрос правильно, ответить имеют право соперники.
При следующем нажатии появляется правильный ответ на вопрос. Для того, чтобы вернуться к игровому полю, необходимо нажать на изображение учёного в правом нижнем углу слайда.
Совершив такой переход, вы сможете увидеть, что сыгравший сектор теперь подсвечен другим цветом.
В случае правильного ответа команде записывается на счёт один балл.
Слайд 4
Не так давно крупные зарубежные издания представили математическую
задачку, которая вызвала бурные обсуждения среди их читателей.
Итак,
чему же равно последнее выражение?
=
2
_
Слайд 5
Не так давно крупные зарубежные издания представили математическую
задачку, которая вызвала бурные обсуждения среди их читателей.
Итак,
чему же равно последнее выражение?
=
2
_
ОТВЕТ
Слайд 6
Самая распространённая ошибка при решении этой задачи –
то, что не все замечают разное количество фруктов в
разных строчках.
Из первого равенства находим, что яблоко равно 10. Подставляем во второе равенство и получаем, что 8 бананов равно 8, т.е. 1 банан равен 1. Из третьего следует, что половина кокоса равна 1. Значит, правильный ответ такой: 3 + 10 + 1 = 14
3 + 10 + 1 = 14
Слайд 7
За минимальное количество перемещений превратите параллелограмм в треугольник.
Слайд 8
За минимальное количество перемещений превратите параллелограмм в треугольник.
ОТВЕТ
Слайд 10
Чем отличаются эти две фотографии Пизанской башни?
Слайд 11
Чем отличаются эти две фотографии Пизанской башни?
ОТВЕТ
Слайд 12
Ничем не отличаются, хоть в это и трудно
поверить.
Из-за особенностей восприятия правая
башня только кажется наклонившейся под большим углом.
Слайд 16
Попробуйте решить задачу, которую знаменитый советский физик, лауреат
Нобелевской премии Лев Ландау предлагал студентам на экзаменах в аспирантуру, но
сам считал, что справиться с ней может только гений или идиот.
Продолжите этот ряд:
р, д, т, ч, п, ш, с, …
Слайд 17
Попробуйте решить задачу, которую знаменитый советский физик, лауреат
Нобелевской премии Лев Ландау предлагал студентам на экзаменах в аспирантуру, но
сам считал, что справиться с ней может только гений или идиот.
Продолжите этот ряд:
р, д, т, ч, п, ш, с, …
ОТВЕТ
Слайд 19
Перед вами кувшин сока и пустой стакан. Больше
ничего нет.
Необходимо наполнить стакан до краёв, но в кувшине
должно остаться столько же сока, сколько было в начале. Как это сделать?
Слайд 20
Перед вами кувшин сока и пустой стакан. Больше
ничего нет.
Необходимо наполнить стакан до краёв, но в кувшине
должно остаться столько же сока, сколько было в начале. Как это сделать?
ОТВЕТ
Слайд 21
Все очень просто. Напиток следует перелить в стакан,
а затем установить его в середину кувшина.
Слайд 22
Из восьми букв, приведённых ниже, можно составить десятки
слов.
А какое максимальное количество слов можете составить вы?
Слайд 23
Из восьми букв, приведённых ниже, можно составить десятки
слов.
А какое максимальное количество слов можете составить вы?
ОТВЕТ
Слайд 24
Вечность, сочень, светоч, честь, сонет, совет, отсев, отвес,
осень, весть, четь, течь, тень, стон, соте, сонь, сечь,
сеть, сено, свет, ость, овен, ночь, новь, енот, вонь, внос, вето, вес, вено, тон, сто, сот, сон, сет, сев, ось, ост, нос, вес.
Слайд 25
У Пушкина есть «x».
У Лермонтова также есть «х»,
но он связан с указанием времени.
Ленинград – это тоже
«х».
Что же такое «х»?
Слайд 26
У Пушкина есть «х».
У Лермонтова также есть «х»,
но он связан с указанием времени.
Ленинград – это тоже
«х».
Что же такое «х»?
ОТВЕТ
Слайд 27
Слово «ГЕРОЙ».
У Пушкина есть стихотворение «Герой», Лермонтов написал
роман «Герой нашего времени», а Ленинград в 1965 году
получил звание «Город-Герой».
Слайд 28
Это фотоснимок был сделан «Brown, Barnes & Bell
Photo Agency» в Ливерпуле в начале XX века. Как
вы думаете, что изображено на фотографии?
Слайд 29
Это фотоснимок был сделан «Brown, Barnes & Bell
Photo Agency» в Ливерпуле в начале XX века. Как
вы думаете, что изображено на фотографии?
ОТВЕТ
Слайд 30
Если повернуть фотографию, то без труда можно увидеть
спящую собаку.
Слайд 31
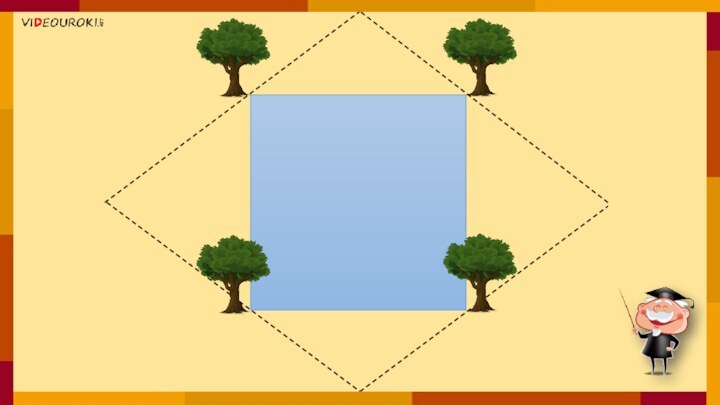
Как расширить пруд?
Имеется квадратный пруд, по берегам которого
растут четыре дерева.
Со временем пруд понадобилось расширить, увеличив его
в два раза и сохранив при этом его квадратную форму.
Каким образом можно расширить пруд, чтобы деревья остались невредимыми, и, как и прежде, оставались расти по берегам пруда?
Слайд 32
Как расширить пруд?
Имеется квадратный пруд, по берегам которого
растут четыре дерева.
Со временем пруд понадобилось расширить, увеличив его
в два раза и сохранив при этом его квадратную форму.
Каким образом можно расширить пруд, чтобы деревья остались невредимыми, и, как и прежде, оставались расти по берегам пруда?
ОТВЕТ
Слайд 34
Переставьте три спички так, чтобы рыбка поплыла в
другом направлении?
Слайд 35
Переставьте три спички так, чтобы рыбка поплыла в
другом направлении?
ОТВЕТ
Слайд 37
Перед вами плакат мебельной компании «Bisley»
Что изображено
на левой его половине?
Слайд 38
ОТВЕТ
Перед вами плакат мебельной компании «Bisley»
Что изображено
на левой его половине?
Слайд 39
Реклама говорит: «Всё должно быть разобрано по порядку»,
тем самым повторяя пословицу английских мебельщиков: «Всему своя полочка».
Слайд 45
С = 1345; В = 2440.
Первым делом складываете
два числа в нижнем ряду: 198 + 263 =
461.
Получилась сумма, которая больше числа, что стоит над ними: 461 > 446.
Вычитаете из большего меньшее: 461 - 446 = 15.
Точно так же считаем остальные пары и видим, что везде получается 15.
Это и есть ключ к решению.
Слайд 46
Эта логическая задача была придумана шахматистом Максом Базелем
в 1848 г.
Попробуйте расставить на шахматной доске восемь ферзей
таким образом, чтобы ни один из них не стоял по диагонали или на прямой линии с другими.
Слайд 47
Эта логическая задача была придумана шахматистом Максом Базелем
в 1848 г.
Попробуйте расставить на шахматной доске восемь ферзей
таким образом, чтобы ни один из них не стоял по диагонали или на прямой линии с другими.
ОТВЕТ