- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Разработка методических рекомендаций обучения решению заданий с развернутым ответом, критерии оценки заданий по решению геометрических задач типа С
Содержание
- 2. Выбор темы обусловлен необходимостью развития у старшеклассников
- 3. Актуальность выбора данной темы состоит в том,
- 4. Актуальность выбора данной темы состоит в том,
- 5. Актуальность выбора данной темы состоит в том,
- 6. способствует повторению всего курса математики 5-11 классов:вычислений,
- 7. Основной проблемой для учащихся при решении планиметрических
- 8. Для повышения качества навыков учащихся в отношении
- 9. Подготовка учащихся к решению планиметрических задач типа
- 10. Решение на ЕГЭ планиметрических задач типа С4
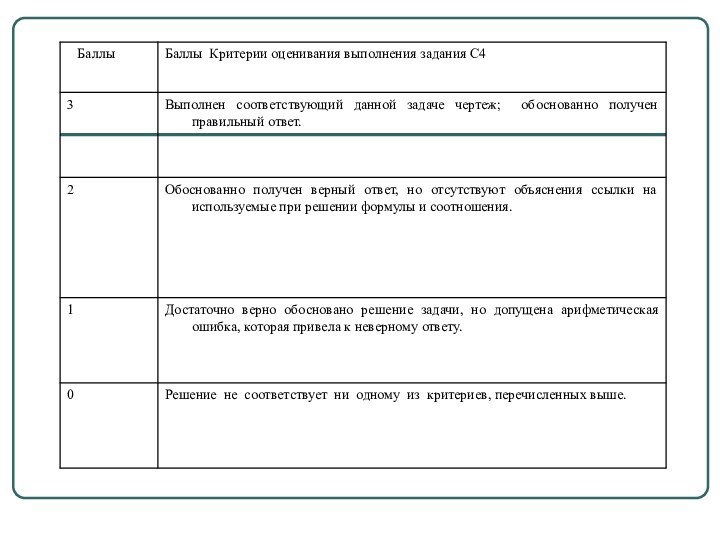
- 11. Критерии оценивания выполнения задания С4 3 балла:
- 12. Для обеспечения качества решения планиметрических задач
- 13. Параллелограмм: определение, свойства сторон, углов и диагоналей;
- 14. Для формирования навыков полного обоснования решения не
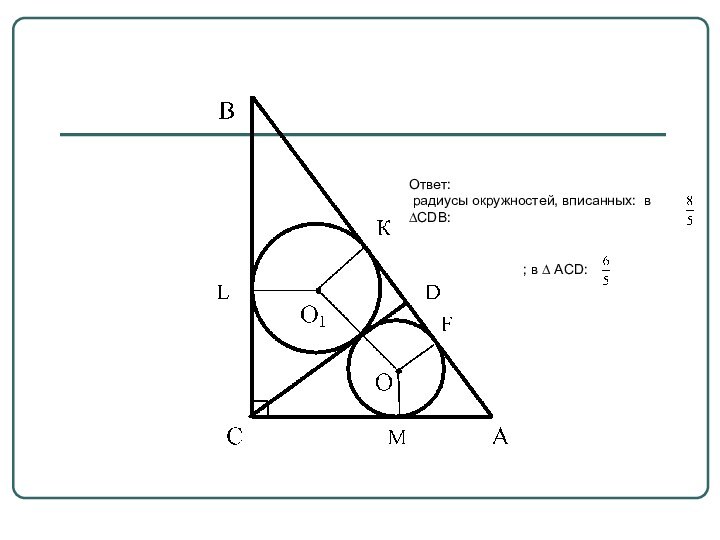
- 15. Задача 1 В прямоугольном треугольнике катеты равны
- 16. План решенияСоставить с учениками необходимый чертеж;Проанализировать условие
- 17. Ответ: радиусы окружностей, вписанных: в ∆CDB:; в ∆ ACD:
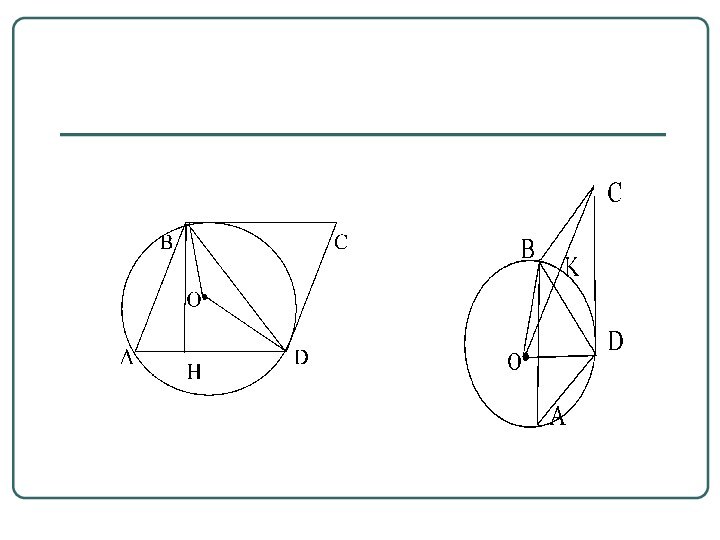
- 20. Задача 2 В параллелограмме ABCD острый угол
- 21. План решения задачи:Рассмотреть разные случаи, выполнив рисунки
- 25. Скачать презентацию
- 26. Похожие презентации
Выбор темы обусловлен необходимостью развития у старшеклассников геометрического воображения, логического, критического и абстрактного мышления, способности к анализу, исследованию задач курса планиметрии, поиску их верного решения.





















Слайд 3
Актуальность выбора данной темы состоит в том, что
повышение качества знаний и умений учащихся по решению задач
планиметрического типа, предполагающее обеспечение теоретической базы по материалу:свойства треугольников, параллелограмма, многоугольников;
окружность, свойства касательных, хорд, вписанных и описанных углов;
площади фигур;
свойства медианы, высоты, биссектрисы
и других теоретических аспектов геометрических знаний, способствует повторению всего курса математики 5-11 классов:
Слайд 4
Актуальность выбора данной темы состоит в том, что
повышение качества знаний и умений учащихся по решению задач
планиметрического типа, предполагающее обеспечение теоретической базы по материалу:свойства треугольников, параллелограмма, многоугольников;
окружность, свойства касательных, хорд, вписанных и описанных углов;
площади фигур;
свойства медианы, высоты, биссектрисы
и других теоретических аспектов геометрических знаний, способствует повторению всего курса математики 5-11 классов:
Слайд 5 Актуальность выбора данной темы состоит в том, что
повышение качества знаний и умений учащихся по решению задач
планиметрического типа, предполагающее обеспечение теоретической базы по материалу:свойства треугольников, параллелограмма, многоугольников;
окружность, свойства касательных, хорд, вписанных и описанных углов;
площади фигур;
свойства медианы, высоты, биссектрисы
и других теоретических аспектов геометрических знаний
Слайд 6
способствует повторению всего курса математики 5-11 классов:
вычислений, формул
сокращенного умножения, решения квадратных уравнений;
решения рациональных, иррациональных, тригонометрических уравнений
и их систем;использование свойств степени с рациональным показателем;
использование свойств тригонометрических функций.
Слайд 7 Основной проблемой для учащихся при решении планиметрических задач
является: во-первых, недостаточное геометрическое воображение, позволяющее «видеть» задачу ,
выделить основные аспекты геометрии, на которые необходимо ссылаться при ссылке на теоретические сведения; во – вторых, недостаточная теоретическая база знаний из курса геометрии 7-9 классов ,позволяющая найти необходимое и достаточное для поиска верного решения задачи. Кроме того, именно в планиметрических задачах типа С ученик может потерять баллы из-за недостаточно полного пояснения хода решения.Слайд 8 Для повышения качества навыков учащихся в отношении решения
планиметрических задач типа С, необходимо при их подготовке к
ЕГЭ обеспечить достаточную теоретическую базу знаний, развивать геометрическое воображение через рассмотрение разных случаев и разных способов решения задач. Для этого учителю необходимо развивать у учеников способности к анализу и синтезу; систематизировать имеющиеся у них знания о представлениях и различных свойствах плоских фигурах.Слайд 9 Подготовка учащихся к решению планиметрических задач типа С
с развернутым ответом на ЕГЭ по математике, прежде
всего, предполагает:основательное обеспечение теоретической базы знаний курса геометрии 7- 9 класса;
развитие геометрического воображения, логики, критического и абстрактного мышления,
формирование практических навыков решения задач повышенной сложности об углах, окружностях, многоугольниках, взаимном расположении геометрических фигур на плоскости.
Слайд 10 Решение на ЕГЭ планиметрических задач типа С4 включает
такие параметры как:
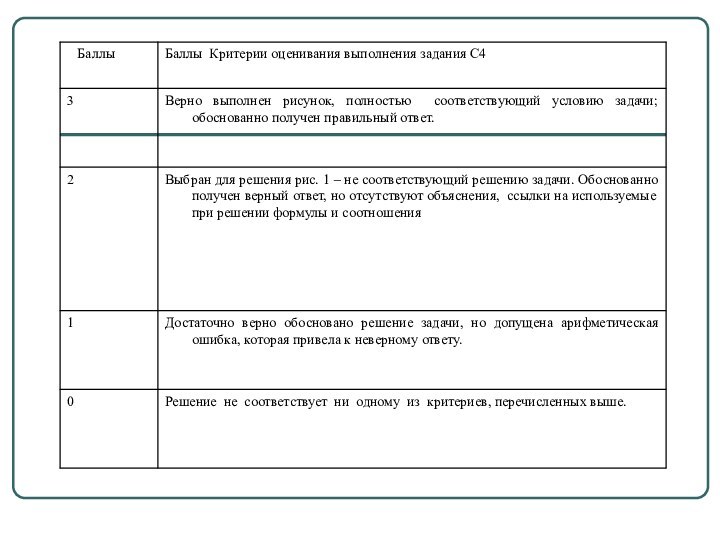
верно изображенный чертеж, с учетом всех
случаев, если возможных решений предусмотрено более одного, позволяющий ученику «увидеть» задачу и быстро определить ход её решения;четкое обоснование решения со ссылкой на теоретические сведения – аксиомы, леммы, теоремы и следствия из них, определяющие свойства планиметрических фигур и их взаимного расположения;
развернутый точный ответ на конкретно поставленный вопрос задачи.
Слайд 11
Критерии оценивания выполнения задания С4
3 балла: рассмотрены
все возможные геометрические конфигурации и обоснованно получен правильный ответ.
2
балла:рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой обоснованно получено правильное значение искомой величины.1 балл: рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неверное из-за арифметической ошибки.
0 баллов: решение не соответствует ни одному из критериев, перечисленных выше.
Слайд 12 Для обеспечения качества решения планиметрических задач учителю
нужно при повторении материала систематизировать теоретические сведения по направлениям:
Треугольники
Прямоугольный
треугольник: теорема Пифагора; связь высоты к гипотенузе треугольника и его катетов с проекциями катетов на гипотенузу; свойство медианы, проведенной к гипотенузе; подобие прямоугольных треугольников; определение синуса, косинуса и тангенса углов.Равносторонний и равнобедренный треугольник: свойства медианы; углов;
Сумма углов треугольника; внешний угол; равенство и подобие треугольников; теорема синусов и следствие из неё; теорема косинусов; свойство биссектрисы; вписанные и описанные окружности; взаимосвязь радиусов вписанной и описанной окружностей с площадью треугольника; средняя линия треугольника;
Слайд 13 Параллелограмм: определение, свойства сторон, углов и диагоналей; определения
и свойства ромба, прямоугольника, квадрата; периметр и площадь;
Трапеция:
определение, свойства, определения и свойства равнобедренной, прямоугольной трапеций; свойство средней линии, периметр и площадь; трапеция, вписанная в окружность или описанная вокруг неё;Четырехугольники: вписанные в окружность и описанные;
Правильные многоугольники: радиусы вписанных и описанных окружностей ; площади и периметр; внутренние и внешние углы;
Окружность: свойства касательных, хорд, секущих; вписанные и центральные углы; длина и мера дуги; длина окружности и площадь круга; сектор и сегмент.
Слайд 14
Для формирования навыков полного обоснования решения
не диктовать
ход решения, не подсказывать его, а побуждать к самостоятельному
анализу условия задачи, планированию хода решения;в форме эвристической беседы с учащимися формировать способность к предвидению верного хода решения: для этого – подбирать необходимые и достаточно ёмкие вопросы, способствующие самостоятельному поиску нужного хода решения учащимися;
через систематическое повторение добиться максимального запоминания учащимися теоретических сведений через понимание, а не зазубривание;
во время решения каждой задачи развивать способность к полному, но, в то же время, четкому и грамотному изложению математической мысли, без лишних слов и посторонних теоретических выкладок;
при решении задач обращать внимание на аккуратность и четкость выполнения рисунка к задаче, выделение в нем известных данных и требуемых для нахождения, дополнительные построения.
Слайд 15
Задача 1
В прямоугольном треугольнике катеты равны 6
и 8. Из вершины прямого угла проведена высота CD.
Определите радиусы вписанных окружностей в треугольники ACD и CDB.
Слайд 16
План решения
Составить с учениками необходимый чертеж;
Проанализировать условие задачи:
для этого задать соответствующие вопросы:
- что означает – вписанные
окружности в треугольники ACD и CDB?;- определение и свойства касательных к окружности?;
- свойство перпендикуляров к одной прямой?
- что можно сказать о треугольниках, образованных высотой, проведенной к гипотенузе прямоугольного треугольника?;
- как связаны проекции катетов на гипотенузу, катеты и высота к гипотенузе прямоугольного треугольника из подобия треугольников?;
- какая формула радиуса вписанной в треугольник окружности получена из свойств касательных к окружности? ;
- сколько существует случаев для схематического изображения рисунка в данной задаче?;
- каких данных достаточно и что необходимо найти для поиска ответа?
Сформулировать и обосновать решение задачи, найти верный ответ.
Проанализировать: за что могут быть сняты баллы на ЕГЭ в задаче такого типа.
Слайд 20
Задача 2
В параллелограмме ABCD острый угол при
вершине А равен 300, сторона CD касается окружности радиуса
6, описанной около треугольника ABD . Определите площадь параллелограмма.
Слайд 21
План решения задачи:
Рассмотреть разные случаи, выполнив рисунки (рис.2,
рис. 3);
Проанализировать условие задачи, обозначив наводящие вопросы:
- определение и
свойства параллелограмма?;- теорема о вписанных в окружность углах?;
- определение окружности, описанной вокруг треугольника?;
- сколько существует случаев решения данной задачи?;
- формулы для нахождения площади параллелограмма?;
- каких данных достаточно и что необходимо найти для поиска ответа?























![Презентация Звук [Ц]. Буква Ц (часть первая). презентация к уроку по логопедии (подготовительная группа) по теме](/img/tmb/9/840409/8133fd5d4cf4cce1d6209b82d5748515-210x.jpg)





