Слайд 2
Сходство ФА и КА
Кластерным анализом называется эвристическая математическая
процедура, цель которой является типологическая группировка совокупностей объектов на
основе множества признаков этих объектов.
С математической точки зрения кластерный анализ аналогичен факторному. Если факторный анализ находит латентные переменные, дисперсия которых объясняет дисперсию наблюдаемых переменных, то кластерный анализ ищет объекты, вариацией которых являются единицы выборки.
Социологическое же содержание двух видов анализа различно. Факторный ищет латентные объясняющие факторы, кластерный производит классификацию объектов наблюдения.
Первые обстоятельные и эффективные руководства по кластерному анализу появились в книге Р.Сокэла и П.Снита «Начала численной таксономии». Книга была посвящена биологическому разнообразию.
Слайд 3
Стратегии кластерного анализа
Стратегия кластерного анализа различается в зависимости
от числа объектов, подлежащих классификации.
Небольшое число объектов -
стран, городов, предприятий, продуктов. В этих случаях ставится задача более или менее надежного отнесения каждого объекта к той или иной группе. Здесь чаще всего классифицируется вся генеральная совокупность.
Большое число объектов – жителей города, страны, семей, населенных пунктов. В этих случаях ставится задача более или менее надежного отнесения всех или большей части объектов к той или иной группе. Здесь чаще всего классифицируется вся выборочная совокупность и на основе сделанной классификации делается вывод о возможности классификации генеральной совокупности.
Слайд 4
Возможные результаты анализа
Возможные результаты кластерного анализа
число кластеров заранее
задано. Это случаи, когда классификация носит априорный характер (высокий,
средний и низкий уровень благосостояния) или когда классификация единожды (ранее или с другой группой объектов) уже была проведена.
число кластеров неизвестно и подлежит определению. Это наиболее распространенный случай, когда стоит задача сгруппировать имеющийся массив объектов в заранее неизвестное число кластеров
число кластеров неизвестно, но его определение и не входит в условие задачи, требуется построить так называемое иерархическое дерево исследуемой совокупности. Характерно для небольшого числа объектов измерения. Целью таких исследований, чаще всего, является изучение формирования групп, а не результат.
Слайд 5
Кластерный анализ
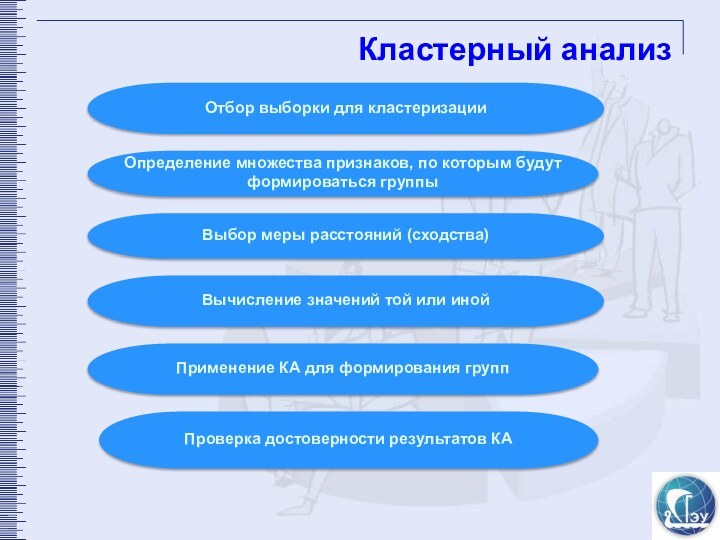
Отбор выборки для кластеризации
Определение множества признаков, по
которым будут формироваться группы
Выбор меры расстояний (сходства)
Вычисление значений той
или иной
Применение КА для формирования групп
Проверка достоверности результатов КА
Слайд 6
Меры близости
Принадлежность отдельной единицы выборки тому или иному
кластеру определяется расстоянием между этой единицей и центром кластера.
Слайд 7
Меры близости
Мер близости и способов вычисления расстояний между
объектами существует великое множество. Наиболее распространенным является евклидово расстояние,
которое лучше всего использовать, когда анализ строится лишь на метрических переменных.
Существуют меры расстояний для частотных шкал (чаще всего хи-квадрат).
Номинальные шкалы переводят в бинарные и используют другие меры близости, например расстояние (мера) Жаккара.
Поскольку меры расстояния – их выбор и исполнение - играют определяющую роль в проведении кластерного анализа, главное значение имеет то, измеряется ли расстояние между двумя объектами до их объединения или после такого объединения.
Слайд 8
Типы кластерного анализа
В первом случае мы имеем иерархические
агломерационные методы. Здесь первый выбранный объект объединяется с тем,
мера близости с которым у него минимальна. В результате получается иерархия, которая начинается с самого близкого объекта и заканчивается самым дальним.
Во втором случае мы имеем дивизионные (разделяющие) методы. В них первоначально массив данных делят на две части, которые максимально отличаются друг от друга (отстоят максимально далеко).
Слайд 9
Иерархические методы анализа
Перед началом кластеризации все объекты считаются
отдельными кластерами, который в ходе алгоритма объединяются.
Вначале мы
имеем N объектов и между ними попарно вычисляются расстояния.
Далее выбирается пара объектов, которые расположены наиболее близко друг к другу, и эти объекты объединяются в один кластер. Теперь мы имеем N-1 кластер и процедура повторяется снова.
На любом этапе объединение можно прервать, удовлетворившись результатом.
Определение числа кластеров остается выбором исследователя, исходя из его целей, характера области исследования и возможностью интерпретации результата.
Также не следует забывать об ограниченной выборке: дробя ее (увеличивая число кластеров), мы снижаем возможности использования произведенной кластеризации.
Слайд 10
Расстояния между кластерами
При вычислении расстояний между двумя объектами,
интерпретация данного параметра однозначна, поскольку объекты носят точечный характер.
Однако,
уже составленный из двух объектов кластер будет иметь несколько характеристик, который можно считать расстоянием до него.
Within-groups linkage – среднее расстояние между всеми парами объектов в кластере
Слайд 11
Расстояния между кластерами
Between-groups linkage – среднее расстояние
Nearest
neighbor – расстояние между ближайшими соседями
Furthest neighbor - расстояние
между далекими соседями
Centroid clustering – расстояние между центрами кластеров.
Ward’s method – расстояние между кластерами как прирост суммы квадратов расстояний между центрами после объединения. Метод построен так, чтобы оптимизировать минимальную дисперсию внутри кластеров.
Слайд 12
Стандартизация
Поскольку кластерный анализ носит эвристический характер, для стандартизаций
помимо традиционной z-стандартизации, используют
Нормирование к диапазону от -1
до 1
Нормирование к диапазону от 0 до 1
Нормирование к максимальному значению, принимаемое за 1
Нормирование к среднему значению, принимаемое за 1
Возможны нелинейные преобразования, например, принять за расстояния их абсолютные значения.
Слайд 13
Пример иерархической дендрограммы
Результат агломеративного метода кластерного анализа наглядно
представляется и легко интерпретируется
Слайд 14
Дивизионные методы (k-means)
Методы слияния очень хороши для случаев,
когда объектов для группировки немного. Каждый из объектов можно
«пощупать», «повертеть» в руках. Можно приложить усилия и собрать дополнительные данные относительно этих объектов.
К тому же процедура объединения на каждом шаге указывает на структуру данных и иерархию объектов.
Однако, все эти достоинства исчезают, если массив данных велик и сами объекты не имеют конкретной привязки в генеральной совокупности.
Среди дивизионных методов чаще других используется метод к-средних. Он прост в реализации и дает легко интерпретируемые результаты.
Слайд 15
Дивизионные методы (k-means)
На первом этапе исследователь задает количество
кластеров – число к и произвольно выбираются к точек,
которые принимаются за центры кластеров.
Затем все объекты распределяются по кластерам в зависимости от расстояния от него до предполагаемого центра кластера.
На третьем этапе вычисляются центры кластеров, полученных в результате объединения N объектов в k кластеров.
На следующем этапе вновь вычисляются расстояния между объектами и центрами получившихся кластеров. Эта операция повторяется до тех пор, пока центры кластеров не стабилизируются. Обычно на это хватает 8-10 итераций.
Если исследователь не удовлетворен результатом группировки, он может задать другое количество кластеров.
Слайд 16
Интерпретация результатов
Главным критерием для удовлетворения результатом КА является
интерпретация его результатов.
Можно ли описать полученную структуру данных?
Существуют ли другие отличия, например, социально-демографические, между объектами, вошедшими в разные кластеры?
Как выбрать число кластеров? – главный вопрос анализа.
Насколько однородны кластеры. Для этого нужно сравнить дисперсии полученных кластеров. Разумеется, дисперсия отдельных кластеров должна быть ниже общей.
Слайд 17
Предостережения
Многие методы кластерного анализа – это довольно простые
(для понимания) процедуры, статистическое обоснование которых еще ждет своего
полноценного решения. Это лишь – правдоподобные алгоритмы группировки.
Методы кластерного анализа разрабатывались для многих научных дисциплин и несут в себе требования к данным, принятым в этих дисциплинах.
Разные кластерные методы могут порождать разные решения для одного и того же массива данных.
Цель кластерного анализа заключается в поиске существующих структур. На самом деле кластерный анализ сам формирует такую структуру, привносит ее в данные.