Слайд 3
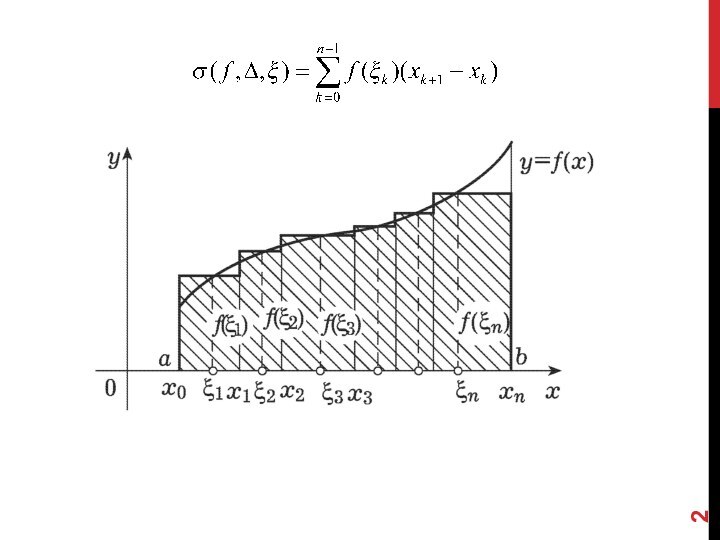
Определение 1. Число I называется пределом интегральных сумм
(f, , ) при () 0; если для
любого положительного числа > 0 можно указать такое положительное число , что для любого разбиения отрезка [a, b] , диаметр разбиения которого меньше : () < , независимо от выбора точек i на отрезках [xk,xk+1], выполняется неравенство
| (f, , ) - I| < .
Слайд 4
Определение 2. Функция f(x) называется интегрируемой (по Риману)
на отрезке [a, b] , если существует конечный предел
I интегральных сумм этой функции при () 0. Указанный предел I называется определенным интегралом от функции f(x) на отрезке [a, b] и обозначается следующим образом:
Слайд 5
Теорема 1. Если функция интегрируема, то она ограничена.
Замечание.
Ограниченность функции не гарантирует ее интегрируемость по Риману
Слайд 6
2.2. Суммы Дарбу и их свойства
Пусть функция f(x)
определена на [a, b] и ={a=x0< x1
отрезка [a, b]. Нижней суммой Дарбу называется сумма
Верхней суммой Дарбу называется сумма
Слайд 8
Определение 3. Если разбиение 2 получено из разбиения
1 добавлением некоторого числа узлов, то говорят, что разбиение
2 следует за разбиением 1 (или 2 является размельчением 1), при этом пишут 1 < 2 .
Слайд 9
Свойства сумм Дарбу:
1) Для любого разбиения и
набора промежуточных точек имеют место соотношения
s(f, )
( f,,) S(f,).
2) Если 1 < 2 два разбиения данного отрезка, то
s(f,1) s(f,2) , S(f,2) S(f,1) .
3) Для любых разбиений 1 ,2 данного отрезка справедливо неравенство
s(f,1) S(f,2).
4) Множество {S} верхних сумм данной функции f(x) для всевозможных разбиений отрезка [а, b] ограничено снизу. Множество {s} нижних сумм ограничено сверху.
Слайд 10
Свойства сумм Дарбу (продолжение):
5) Пусть разбиение 1 отрезка
[а, b] получено из разбиения добавлением к последнему
р новых точек, и пусть s*, S*
и s, S — соответственно нижние и верхние суммы разбиений 1 и . Тогда для разностей S S* и s* s может быть получена оценка, зависящая от максимальной длины частичных сегментов разбиения , числа р добавленных точек и точных верхней и нижней граней М и m функции f(x) на отрезке [а, b]. Именно,
S – S* (M - m)p, s* - s (М - m)р.
6) Лемма Дарбу. Верхний и нижний интегралы Дарбу от функции f(x) на отрезке [а, b] являются соответственно пределами верхних и нижних сумм при 0.


![2. Определенный интеграл Определение 2. Функция f(x) называется интегрируемой (по Риману) на отрезке [a, b]](/img/tmb/13/1236351/7a063f2323eb2cd370869067909b221d-720x.jpg)

![2. Определенный интеграл 2.2. Суммы Дарбу и их свойстваПусть функция f(x) определена на [a, b] и ={a=x0< x1](/img/tmb/13/1236351/c5562c252d632fe0be5b37f72f3b3aa2-720x.jpg)



![2. Определенный интеграл Свойства сумм Дарбу (продолжение): 5) Пусть разбиение 1 отрезка [а, b] получено](/img/tmb/13/1236351/a23111d50edcf07c3fd2a5197c3b00f9-720x.jpg)































