- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Софизмы и парадоксы, 9 класс
Содержание
- 2. Цель и задачи Цель: .Разл1. Изучение понятий софизма
- 3. «Правильно понятая ошибка – это путь к
- 4. Экскурс в историюСофистами называли группу древнегреческих философов
- 5. Однако софизмы существовали задолго до философов-софистов, а
- 6. Первые парадоксы были известны уже в глубокой
- 7. Понятие софизмаСофизм - (от греческого sophisma –
- 8. Понятие парадоксаПарадокс (от греч. paradoxos – неожиданный,
- 9. Парадокс (греч. "пара" - "против", "докса" -
- 10. Отношение к истинеИз определений можно вывести отличие
- 11. Виды парадоксов и софизмовПарадокс
- 12. Классификация софизмов Логические
- 13. Типичные ошибки при решении софизмов Пренебрежение условиями
- 14. Дважды два пятьНапишем тождество 4:4=5:5. Вынесем
- 15. Разбор софизмаОшибка сделана при вынесении общих множителей
- 16. Возьмем уравнение x–a =0Разделив обе его
- 17. Разбор софизма:Ошибка допущена при делении равенства
- 18. Один рубль не равен ста копейкамИзвестно, что
- 19. Разбор софизма:Ошибка, допущенная в этом софизме, состоит
- 20. Полный стакан равен пустому Пусть имеется стакан,
- 21. Разбор софизма:Ясно, что приведенное рассуждение неверно, так
- 22. « Спичка вдвое длиннее телеграфного столба»Пусть а
- 23. Разбор софизма:В выражении b(b-a-c )= -c(b-a-c) производится
- 24. Из точки на прямую можно опустить два
- 25. Разбор софизма: Рассуждения опирались на
- 26. Логические софизмы Лекарства«Лекарство, принимаемое больным, есть добро.
- 27. Парадокс неожиданной казниВас казнят на следующей неделе
- 28. «Парадокс парикмахера»В некой деревне, где жил единственный
- 29. Парадокс вороновПредположим, что существует теория, согласно которой все вороны чёрные.
- 30. «Парадокс кучи»Два приятеля однажды вели такой разговор.
- 31. Вывод:ПАРАДОКС - это два противоположных утверждения, для
- 32. Скачать презентацию
- 33. Похожие презентации
Цель и задачи Цель: .Разл1. Изучение понятий софизма и парадокса.Различие и сходство между ними.Задачи:Познакомиться с парадоксами и софизмами; Понять, как найти ошибку в них.






























Слайд 2
Цель и задачи
Цель:
.
Разл1. Изучение понятий софизма и парадокса.Различие
и сходство между ними.
как найти ошибку в них.
Слайд 4
Экскурс в историю
Софистами называли группу древнегреческих философов 4-5
века до н.э., достигших большого искусства в логике. В
период падения нравов древнегреческого общества( 5 век) появляются так называемые учителя красноречия, которые целью своей деятельности считали и называли приобретение и распространения мудрости, вследствие чего они именовали себя софистами.Слайд 5 Однако софизмы существовали задолго до философов-софистов, а наиболее
известные и интересные были сформулированы позднее в сложившихся под
влиянием Сократа философских школах. Термин "софизм" впервые ввел Аристотель, охарактеризовавший софистику как мнимую, а не действительную мудрость. Характерно, что для широкой публики софистами были также Сократ, Платон и сам АристотельСлайд 6 Первые парадоксы были известны уже в глубокой древности,
существуют и современные парадоксы. Некоторые из этих противоречий удалось
решить путём создания новых теорий, переосмысления устоявшихся, но несовершенных законов. Другие – так и остались неразрешенными. Т.к. парадоксы чаще всего открываются, а не придумываются, сложно рассказать что либо об их истории.
Слайд 7
Понятие софизма
Софизм - (от греческого sophisma – уловка,
ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую
нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям, и имеющееизначально заложенную ошибку.
Слайд 8
Понятие парадокса
Парадокс (от греч. paradoxos – неожиданный, странный)
– мнение, рассуждение, резко расходящееся с общепринятыми понятиями, противоречащее
(иногда только на первый взгляд) здравому смыслу; формально-логическое противоречие, которое возникает в содержательной теории множеств и формальной логике при сохранении логической правильности хода рассуждений;Слайд 9 Парадокс (греч. "пара" - "против", "докса" - "мнение")
близок к софизму. Но от него он отличается тем,
что это не преднамеренно полученный противоречивый результат.Парадокс - странное, расходящееся с общепринятым мнением, высказывание, а также мнение, противоречащее (иногда только на первый взгляд) здравому смыслу (словарь Ожегова).
В широком смысле парадокс - высказывание, истинность которого неочевидна. Парадоксальными называются любые неожиданные противоречивые высказывания.
Математический парадокс – высказывание, которое может быть доказано и как истинна, и как ложь.
Слайд 10
Отношение к истине
Из определений можно вывести отличие между
софизмом и парадоксом: отношение к истине. Несмотря на то,
что и софизм и парадокс доказывают на первый взгляд абсурдные вещи, парадокс это верное утверждение, в то время как софизм изначально ложное. Парадокс – это абсолютная истина, софизм – относительная истина.
Слайд 11
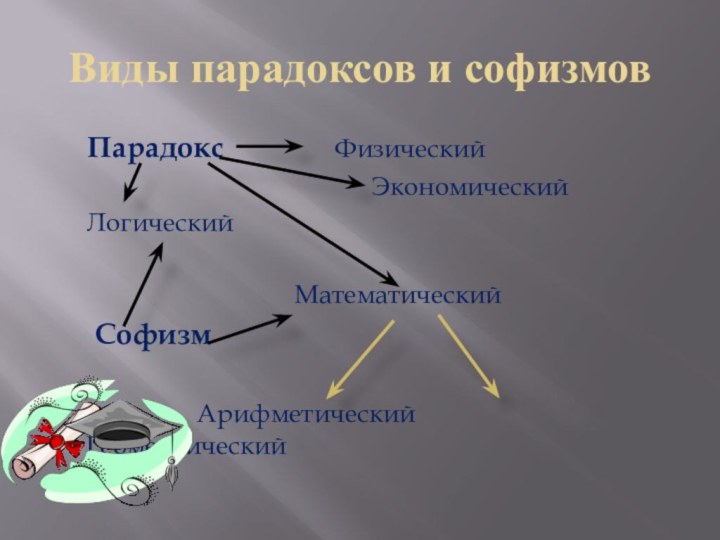
Виды парадоксов и софизмов
Парадокс
Физический
Экономический Логический
Математический
Софизм
Арифметический Геометрический
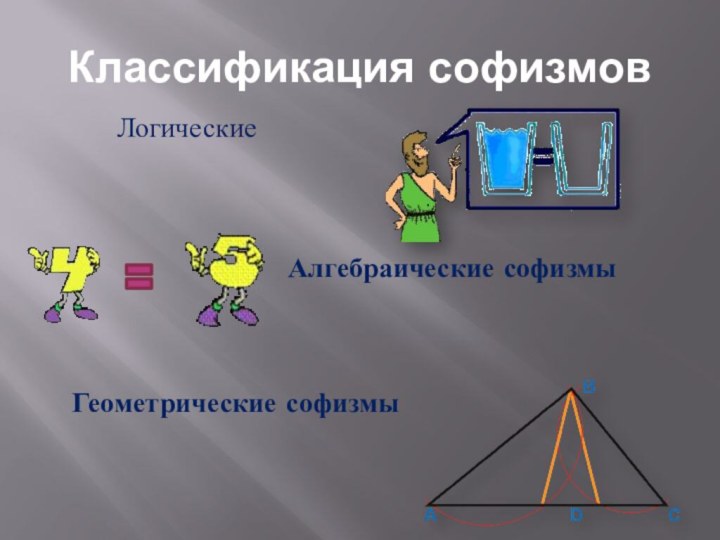
Слайд 13
Типичные ошибки при решении софизмов
Пренебрежение условиями теорем;
формул и правил;
Ошибочный чертеж;
Опора на
ошибочные умозаключения.Запрещенные действия;
Слайд 14
Дважды два пять
Напишем тождество 4:4=5:5.
Вынесем из
каждой части тождества общие множители за скобки, получаем:
4(1:1)=5(1:1)
или (2·2)·(1:1) = 5·(1:1)Так как 1:1=1 , то сократим и получим
2 · 2 = 5
Слайд 15
Разбор софизма
Ошибка сделана при вынесении общих множителей 4
из левой части и 5 из правой.
Действительно, 4:4=1:1,
но 4:4≠4(1:1).Так выносить за скобки нельзя!
Слайд 17
Разбор софизма:
Ошибка допущена при делении равенства
х – а = о на число
х – а, равное 0.На 0 делить нельзя!
Слайд 18
Один рубль не равен ста копейкам
Известно, что любые
два равенства можно перемножить почленно, не нарушая при этом
равенства, т.е. если а = b и c = d, то a·c = b·d.Применим это положение к двум очевидным равенствам: 1 рубль = 100 копейкам и
10 рублей = 1000 копеек
Перемножая эти равенства почленно, получим
10 рублей = 100 000 копеек
и разделив последнее равенство на 10, получим, что
1 рубль = 10 000 копеек
Таким образом,
один рубль не равен ста копейкам.
Слайд 19
Разбор софизма:
Ошибка, допущенная в этом софизме, состоит в
нарушении правила действий с именованными величинами: все действия, совершаемые
над величинами, необходимо совершать также и над их размерностями.
Слайд 20
Полный стакан равен пустому
Пусть имеется стакан, наполненный
водой до половины. Тогда можно сказать, что стакан, наполовину
полный равен стакану наполовину пустому. Увеличивая обе части равенства вдвое, получим, что стакан полный равен стакану пустому.
Слайд 21
Разбор софизма:
Ясно, что приведенное рассуждение неверно, так как
в нем применяется неправомерное действие: увеличение вдвое. В данной
ситуации его применение бессмысленно
Слайд 22
« Спичка вдвое длиннее телеграфного столба»
Пусть а дм-
длина спички и b дм - длина столба. Разность
между b и a обозначим через c .Имеем b - a = c, b = a + c. Перемножаем два эти равенства по частям, находим: b2 - ab = ca + c2. Вычтем из обеих частей bc. Получим: b2- ab - bc = ca + c2 - bc, или b(b - a - c) = - c(b - a - c), откуда
b = - c, но c = b - a, поэтому b = a - b, или a = 2b.
Где ошибка???
Слайд 23
Разбор софизма:
В выражении b(b-a-c )= -c(b-a-c) производится деление
на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит,
спичка не может быть вдвое длиннее телеграфного столба.
Слайд 24
Из точки на прямую можно опустить два перпендикуляра
Попытаемся доказать, что через точку, лежащую вне прямой,
к этой прямой можно провести два перпендикуляра. С этой целью возьмем ∆АВС. На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках Е и D. Соединим точки Е и D прямыми с точкой В. Угол ВЕА – прямой, как вписанный, опирающийся на диаметр угол ВDC также прямой. Следовательно, ВЕ ┴ АС и BD ┴ AC. Через точку В проходят два перпендикуляра к прямой AC.
Слайд 25
Разбор софизма:
Рассуждения опирались на ошибочный
чертеж. В действительности полуокружности пересекаются со стороной АС в
одной точке, т.е. ВЕ совпадает с ВD.Даже если чертеж был бы правильным, то не возможно, что в треугольнике ВЕD сумма всех углов больше 180˚. ( угол Е равен 90˚, угол D равен 90 ˚).
Слайд 26
Логические софизмы
Лекарства
«Лекарство, принимаемое больным, есть добро. Чем больше
делать добра, тем лучше. Значит, лекарств нужно принимать как
можно больше».Вор
«Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего».
Рогатый
«Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога».
Слайд 27
Парадокс неожиданной казни
Вас казнят на следующей неделе в
полдень.
День казни станет для вас сюрпризом, вы узнаете о
нём только когда палач в полдень войдет к вам в камеру.Начальник тюрьмы никогда не врал. Заключённый подумал над его словами: «В воскресенье меня казнить не могут! Ведь тогда уже в субботу вечером я буду знать об этом. Последовательно исключив субботу, пятницу, четверг, среду, вторник и понедельник преступник пришел к выводу, что начальник не сможет его казнить. На следующей неделе палач постучал в его дверь в полдень в среду — это было для него полной неожиданностью.
Слайд 28
«Парадокс парикмахера»
В некой деревне, где жил единственный парикмахер-мужчина,
был издан указ: "Парикмахер имеет право брить тех и
только тех жителей деревни, которые не бреются сами". Спрашивается, может ли парикмахер брить сам себя?Как будто не может, поскольку это запрещено указом.
И вместе с тем, если он не бреет себя, значит, попадает в число тех жителей, которые не бреются сами, а таких людей парикмахер имеет право брить.
Слайд 29
Парадокс воронов
Предположим, что существует теория, согласно которой все вороны чёрные. Согласно
формальной логике все предметы, не являющиеся чёрными, не являются воронами.
Если человек увидит много чёрных воронов, то его уверенность в том, что эта теория верна, увеличится. Если же он увидит много красных яблок, то это увеличит его уверенность в том, что все не чёрные предметы не являются воронами, и также увеличит его уверенность в том, что все вороны чёрные.
Слайд 30
«Парадокс кучи»
Два приятеля однажды вели такой разговор.
-
Видишь кучу песка? - спросил первый. - Я-то
её вижу, - ответил второй, - но её нет на самом деле.- Почему? - удивился первый.
- Очень просто, - ответил второй. - Давай рассудим: одна песчинка, очевидно, не образует кучи песка. Если n песчинок не могут образовать кучи песка, то и после прибавления ещё одной песчинки они по-прежнему не могут образовать кучи. Следовательно, никакое число песчинок не образует кучи, т. е. кучи песка нет.
Слайд 31
Вывод:
ПАРАДОКС - это два противоположных утверждения, для каждого
из которых имеются кажущиеся убедительными аргументы.
Парадокс в более
узком и более современном значении – это два противоположных утверждения, для каждого из которых имеются убедительные аргументы.Софизмы являются логически неправильными рассуждениями, выдаваемыми за правильные и доказательные.
Софизм – это обман. Но обман тонкий и закамуфлированный, так что его не сразу и не каждому удается раскрыть.