Презентация на тему по алгебре на тему Четные и нечетные функции. Периодичность функций. (10 класс)

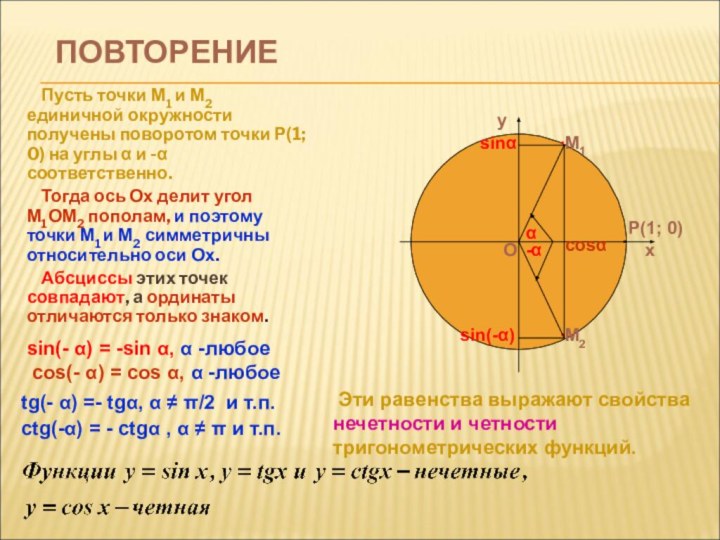
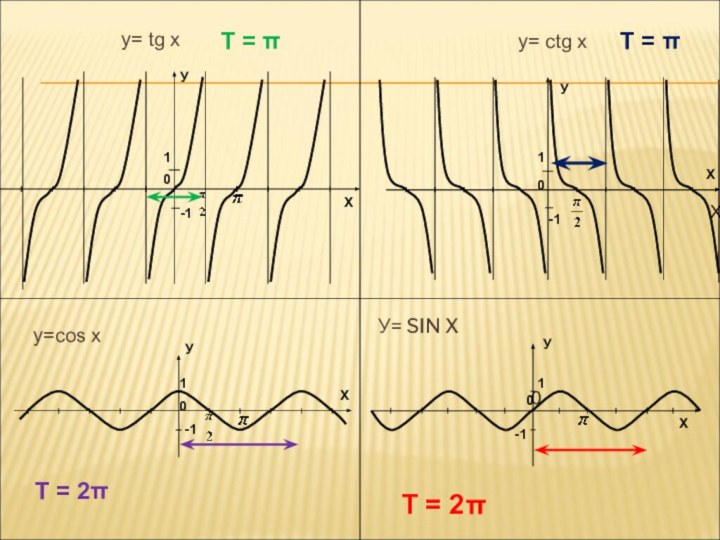
формулы определения четности и нечетности функций, периодичности функций
Узнать основные

тригонометрические формулы
Узнать, где в жизни применяется знание тригонометрии
Научиться применять новые формулы на практике
Научиться пользоваться ранее изученными формулами на практике

II – НЕЧЕТНЫХ.

3,6,7

2, 4, 8

график симметричен относительно оси ординат.
Функция нечетна тогда и только

тогда, когда её график симметричен относительно начала координат.

поворотом точки Р(1; 0) на углы α и -α

соответственно.
Тогда ось Ох делит угол М1ОМ2 пополам, и поэтому точки М1 и М2 симметричны относительно оси Ох.
Абсциссы этих точек совпадают, а ординаты отличаются только знаком.

∙М2

∙М1

-α

α

sinα

sin(-α)

cosα

tg(- α) =- tgα, α ≠ π/2 и т.п.
ctg(-α) = - ctgα , α ≠ π и т.п.

sin(- α) = -sin α, α -любое cos(- α) = cos α, α -любое

Эти равенства выражают свойства нечетности и четности тригонометрических функций.

= x⁴; f(x) = x; f(x) = x³; f(x)

= x⁵;
f(x) = |x|; f(x) = cos x; f(x) = sin x


f(x) = 2x⁴ + cos² x
f(x) = x³ - sin x

?

= f(x) – четная функция

f(- x) = - f(x) – нечетная функция


f(x) = 2x⁴ + x²
f(2) = 2(2)⁴ + 2² = 2*16 + 4 = 36
f(-x) = 2(-x)⁴ + (-x)² = 2x⁴ + x² = f(x) – четная функция

+ cos² x
f(x) = x³ - sin x

f(-x) =

2(-x)⁴ + cos²(-x) = 2x⁴ + cos² x = f(x) – четная
f(-x) = (-x)³ - sin(-x) = -x³ + sin x = -(x³ - sin x) = -f(x)- нечетная

Придумай любую функцию и проверь ее на четность или нечетность?

является ни четной, ни нечетной
да
нет
да

нет
Составь по этой схеме алгоритм

определения четности или нечетности функции

или нечетной:

ни четными, ни нечетными
f(x) = 3sin 2x²
f(x) = sin

x – x
f(x) = |tg x|
f(x) = ctg 3x +tg x
f(x) = x² + ctg x
f(x) = cos x * sin 2x

Всего 15 маятников, самый длинный маятник

делает 51 колебание в минуту, каждый последующий — на одно колебание в минуту больше, т.е. последний, самый короткий маятник, делает 65 колебаний за 60 секунд. Период у каждого зависит от корня длины верёвки, но не зависит от амплитуды (слабо отклонённый шарик будут иметь один период... сильно отклонённый быстрее "качается")

кривой, называемой косинусом.

значений повторяется раз за разом, и точки с одинаковыми

значениями функции расположены на числовой оси с равными промежутками. Это расстояние и будем называть периодом.
Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным.

y=f(x)

Графики периодических функций:

Т

T

T

x
T = π
T = π
T = 2π
T = 2π

sin (kx + b) и f(x) = А

cos (kx + b)
f(x) = sin 3x T = 2π/3
f(x) = cos(5x + 2) T = 2π/5
f(x) = 7sin(-9x – 1) T = 2π/9
f(x) = tg 7x T = π/7
f(x) = tg(-5x + 2) T = π/5
f(x) = 2ctg (3x – 4) T = π/3
f(x) = sin(4x + 7) T = π/2
T' = T/|k|

человека, дату отсчета (день, месяц, год) и длительность прогноза

(кол-во дней).

её график симметричен относительно оси ординат.
Функция нечетна тогда и

только тогда, когда её график симметричен относительно начала координат.
f(- x) = f(x) – четная функция
f(- x) = - f(x) – нечетная функция
Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным:
y=sin x T =2π y=cos x

y=tg x T = π y=ctg x

T' = T/|k| - формула для вычисления периодов функций у = f(kx +b)

окружающем нас мире и жизни человека»:
Цель: связь тригонометрии с

реальной жизнью
Задачи:
Узнать, где тригонометрия применяется в жизни(в каких областях)?
Ответить на вопрос: «Пригодятся ли тебе знания тригонометрии в жизни?»

урока?
Достигли ли мы цели?
Понравился ли тебе урок?
Что ты узнал

нового на уроке?
Возникли ли у тебя какие-нибудь трудности при выполнении заданий?
Если возникли, то как их преодолеть?
Понятно ли тебе домашнее задание?