находим:
или
2) Пусть
либо
3) Если
Ответ:
ОДЗ: у > 0
(не удовлетворяет ОДЗ).
(не удовлетворяет ОДЗ).
, тогда либо
тогда
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку - практикуму (подготовка к ЕГЭ)
Содержание
- 2. №1.Решите систему уравнений(задание №13, ЕГЭ, профиль)Решение.1) Из
- 3. №2. В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого
- 4. №3. Решите неравенство (задание №15, ЕГЭ, профиль)Решение.Решение
- 5. №4. Дана трапеция АВСD, основания которой ВС=44,
- 6. Дана трапеция АВСD, основания которой ВС=44, AD=100,
- 7. Дана трапеция АВСD, основания которой ВС=44, AD=100,
- 8. Решение.Изобразим графики левой и правой частей неравенства
- 9. Решение.ху-10..-3Заметим, что неравенство не имеет решения при -4
- 10. Решение.ху-10..-3Раскрывая знак модуля на каждом интервале, получим:По
- 11. Скачать презентацию
- 12. Похожие презентации
№1.Решите систему уравнений(задание №13, ЕГЭ, профиль)Решение.1) Из уравнения находим:или2) Пусть либо 3) ЕслиОтвет: ОДЗ: у > 0(не удовлетворяет ОДЗ).(не удовлетворяет ОДЗ)., тогда либотогда
Слайд 2
№1.Решите систему уравнений
(задание №13, ЕГЭ, профиль)
Решение.
1) Из уравнения
Слайд 3
№2. В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AB
= 6, BC = 6, CC1 = 4, найдите
тангенс угла между плоскостями ACD1 и A1B1C1. (Часть задания №14, ЕГЭ, профиль)
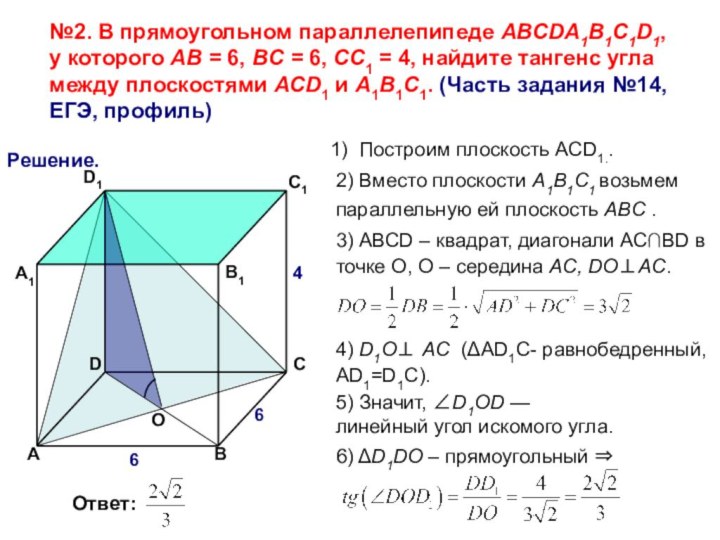
4) D1О⊥ AC (ΔAD1C- равнобедренный, AD1=D1C).
Решение.
2) Вместо плоскости A1B1C1 возьмем параллельную ей плоскость ABC .
1) Построим плоскость ACD1..
3) АВСD – квадрат, диагонали АС∩BD в точке О, О – середина AC, DО⊥AC.
5) Значит, ∠D1ОD —
линейный угол искомого угла.
6) ΔD1DО – прямоугольный ⇒
Слайд 4
№3. Решите неравенство (задание №15, ЕГЭ, профиль)
Решение.
Решение неравенства
ищем при условиях:
Рассмотрим два случая:
и, значит, x = 2
или x = 4.Откуда, x = 2 — решение задачи
1)
2)
, разделив обе части неравенства на общий
множитель получим:
х
(так как х = 4 не удовлетворяет ОДЗ).
С учетом ограничений получаем:
Ответ:
Слайд 5 №4. Дана трапеция АВСD, основания которой ВС=44, AD=100,
AB=CD=35. Окружность, касающаяся прямых AD и АС, касается стороны
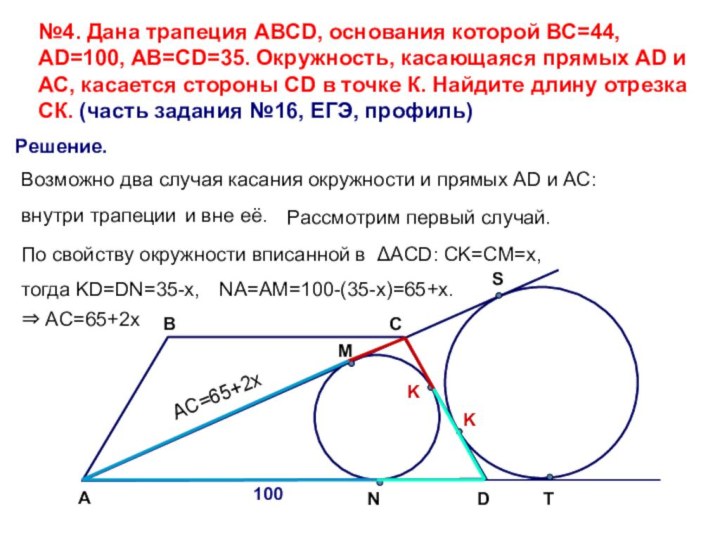
CD в точке К. Найдите длину отрезка СК. (часть задания №16, ЕГЭ, профиль)Решение.
Возможно два случая касания окружности и прямых AD и АС:
внутри трапеции
и вне её.
Рассмотрим первый случай.
По свойству окружности вписанной в ΔACD: CK=CM=x,
тогда KD=DN=35-x,
⇒ AC=65+2x
AC=65+2x
NA=AM=100-(35-x)=65+x.
100
Слайд 6
Дана трапеция АВСD, основания которой ВС=44, AD=100, AB=CD=35.
Окружность, касающаяся прямых AD и АС, касается стороны CD
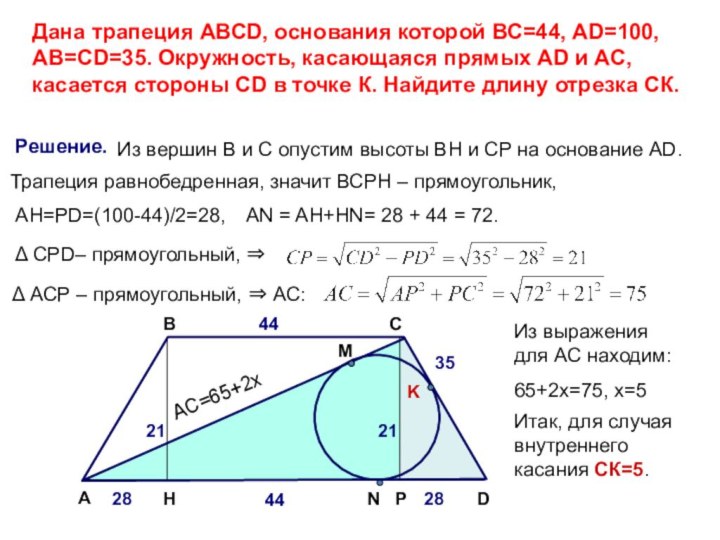
в точке К. Найдите длину отрезка СК.Решение.
Н
Р
Из вершин В и С опустим высоты BH и CP на основание AD.
Δ CPD– прямоугольный, ⇒
Δ АСР – прямоугольный, ⇒ АС:
35
AH=PD=(100-44)/2=28,
Трапеция равнобедренная, значит ВСРН – прямоугольник,
AN = AH+HN= 28 + 44 = 72.
AC=65+2x
Из выражения для АС находим:
65+2х=75, х=5
Итак, для случая внутреннего касания СК=5.
Слайд 7 Дана трапеция АВСD, основания которой ВС=44, AD=100, AB=CD=35.
Окружность, касающаяся прямых AD и АС, касается стороны CD
в точке К. Найдите длину отрезка СК.Решение.
Рассмотрим второй случай.
Пусть CS=CK=x,
ТA=AS=100+(35-x)=135-x, с другой стороны,
AS=AC+CS=AC + x.
Получаем уравнение:
75 + х = 135 – х, ⇒ х = 30
Итак, во втором случае СК=30.
Ответ: 5 или 30.
тогда KD=DТ=35-x,
75
х
100
35-х
Слайд 8
Решение.
Изобразим графики левой и правой частей неравенства
х
у
-1
0
Неподвижный
«прямой угол» с вершиной в точке (-3; -1), лучи
которого направлены вверх..
.
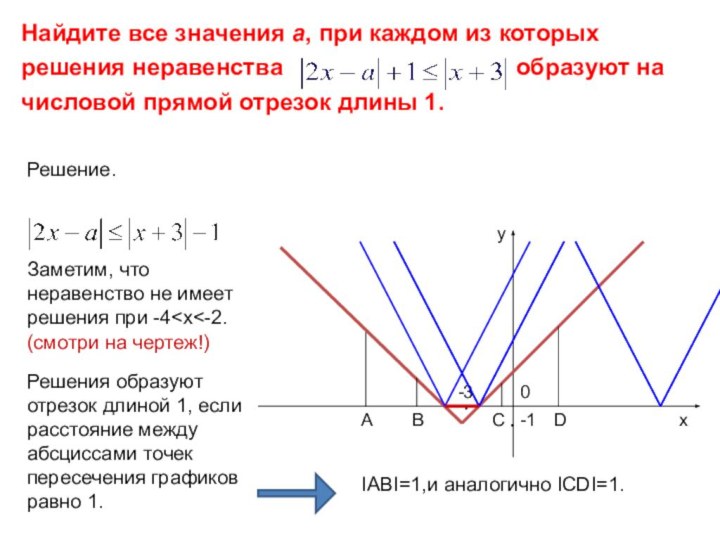
-3
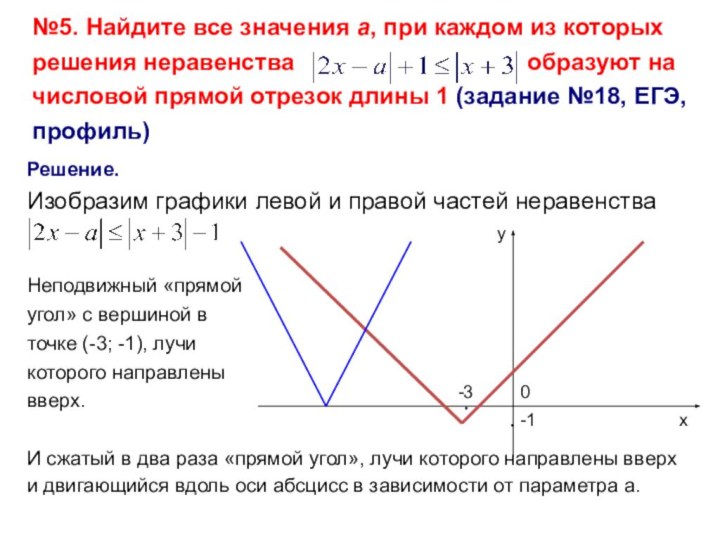
И сжатый в два раза «прямой угол», лучи которого направлены вверх и двигающийся вдоль оси абсцисс в зависимости от параметра а.
Слайд 9
Решение.
х
у
-1
0
.
.
-3
Заметим, что неравенство не имеет решения при -4
образуют отрезок длиной 1, если расстояние между абсциссами точек
пересечения графиков равно 1.(смотри на чертеж!)
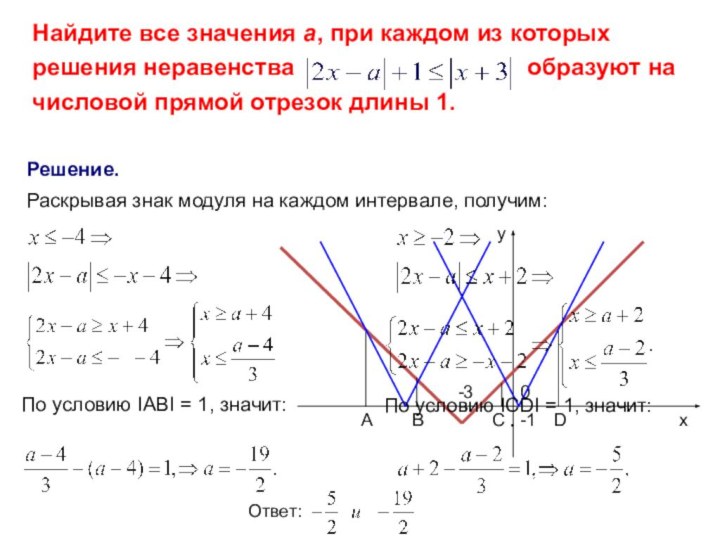
IABI=1,и аналогично ICDI=1.
Слайд 10
Решение.
х
у
-1
0
.
.
-3
Раскрывая знак модуля на каждом интервале, получим:
По условию
