- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему 11 класс задание №7 профиля
Содержание
- 2. Прямая у = 6х+9 параллельна касательной к
- 3. 2. Прямая у=2х является касательной к графику функции у=х3+5х2+9х+3 . Найдите абсциссу точки касания.
- 4. 3. На рисунке изображен график производной функции
- 5. Производная функции в точке х0 равна 0
- 6. На рисунке изображен график функции y
- 7. 5. На рисунке изображен график функции
- 8. На рисунке изображен график функции y
- 9. 6. На рисунке изображён график y=f′(x) —
- 10. 7. На рисунке изображён график y=f′(x) —
- 11. 8. На рисунке изображен график производной
- 12. 9. На рисунке изображен график производной функции
- 13. На рисунке изображен график производной функции
- 14. В точке минимума производная функции равна нулю
- 15. 11. На рисунке изображен график производной
- 16. 12. На рисунке изображен график производной
- 17. 13. На рисунке изображен график производной функции
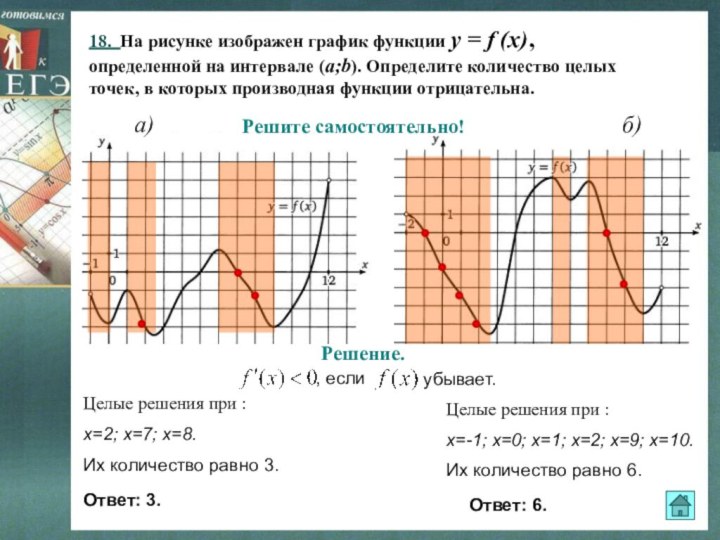
- 18. 14. На рисунке изображен график функции
- 19. На рисунке изображен график функции y =
- 20. 15. На рисунке изображен график функции y
- 21. 16. На рисунке изображен график функции
- 22. На рисунке изображен график функции y
- 23. 17. На рисунке изображен график функции y
- 24. Скачать презентацию
- 25. Похожие презентации



Слайд 3 2. Прямая у=2х является касательной к графику функции
у=х3+5х2+9х+3 . Найдите абсциссу точки касания.
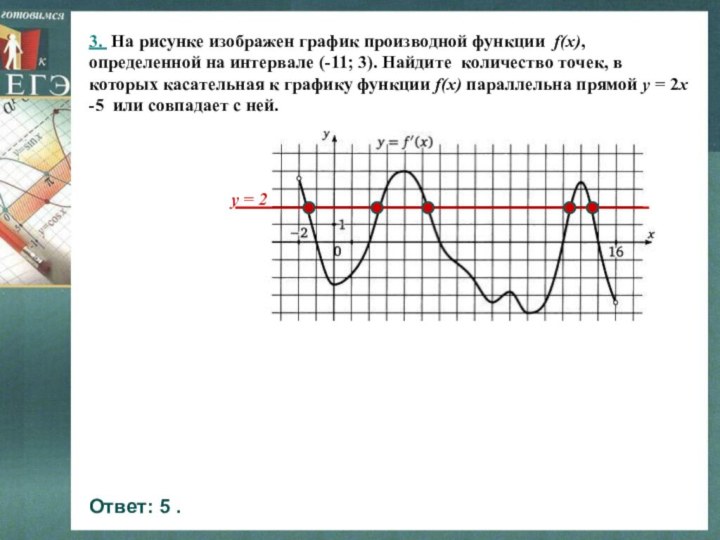
Слайд 4 3. На рисунке изображен график производной функции f(x),
определенной на интервале (-11; 3). Найдите количество точек, в
которых касательная к графику функции f(x) параллельна прямой y = 2x -5 или совпадает с ней.y = 2
Ответ: 5 .
Слайд 5 Производная функции в точке х0 равна 0 тогда
и только тогда, когда касательная к графику функции, проведенная
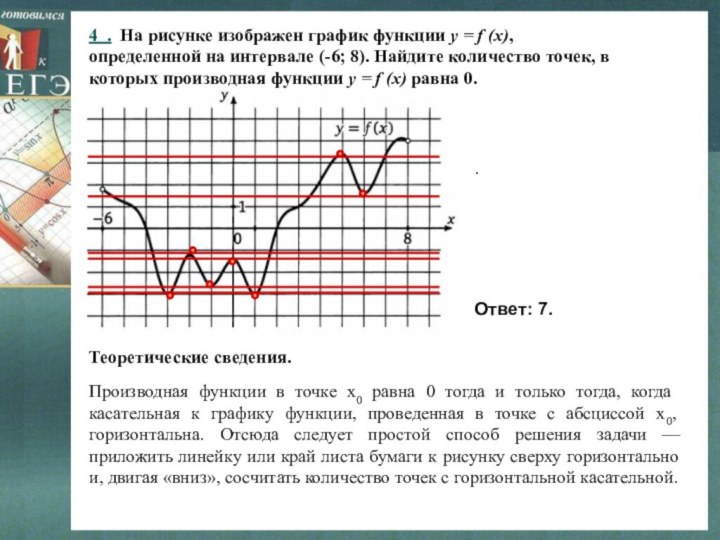
в точке с абсциссой х0, горизонтальна. Отсюда следует простой способ решения задачи — приложить линейку или край листа бумаги к рисунку сверху горизонтально и, двигая «вниз», сосчитать количество точек с горизонтальной касательной.4 . На рисунке изображен график функции y = f (x),
определенной на интервале (-6; 8). Найдите количество точек, в
которых производная функции y = f (x) равна 0.
Теоретические сведения.
.
Ответ: 7.
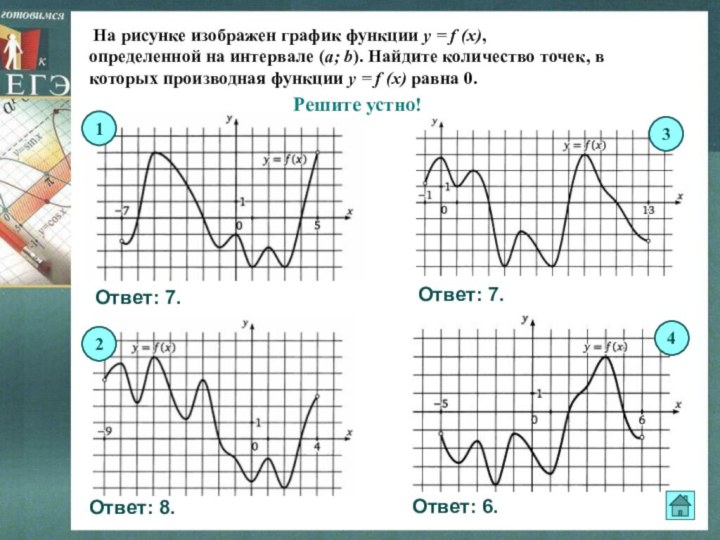
Слайд 6 На рисунке изображен график функции y =
f (x),
определенной на интервале (a; b). Найдите количество точек,
в которых производная функции y = f (x) равна 0.
Решите устно!
Ответ: 7.
Ответ: 7.
Ответ: 8.
Ответ: 6.
1
3
4
2
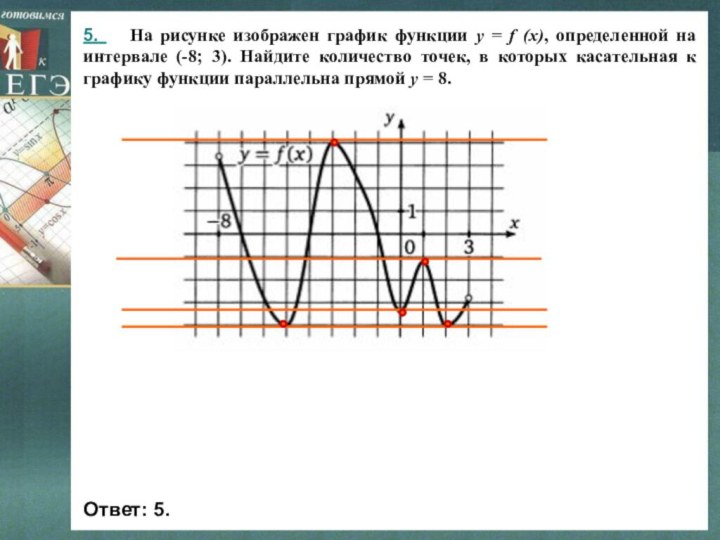
Слайд 7 5. На рисунке изображен график функции y
= f (x), определенной на интервале (-8; 3). Найдите
количество точек, в которых касательная к графику функции параллельна прямой у = 8.Ответ: 5.
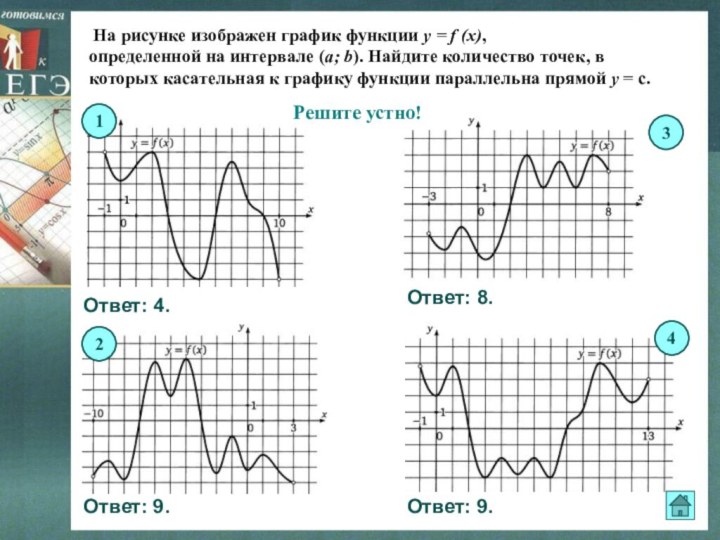
Слайд 8 На рисунке изображен график функции y =
f (x),
определенной на интервале (a; b). Найдите количество точек,
в которых касательная к графику функции параллельна прямой у = с.
1
3
4
2
Решите устно!
Ответ: 4.
Ответ: 9.
Ответ: 8.
Ответ: 9.
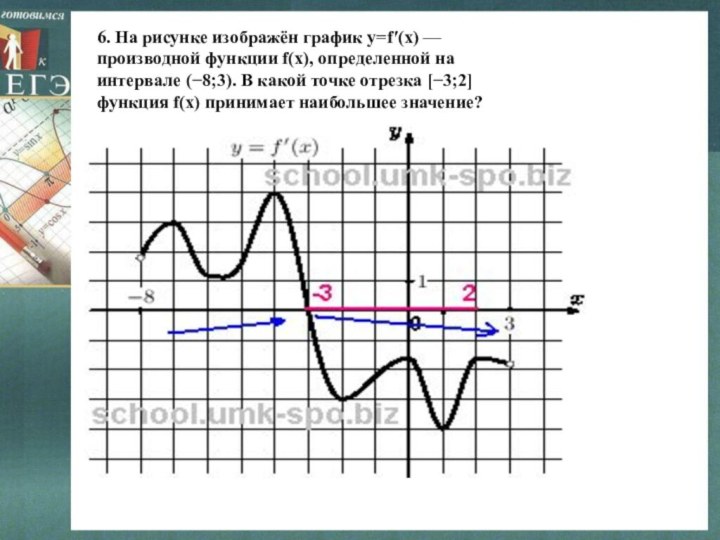
Слайд 9 6. На рисунке изображён график y=f′(x) — производной
функции f(x), определенной на интервале (−8;3). В какой точке
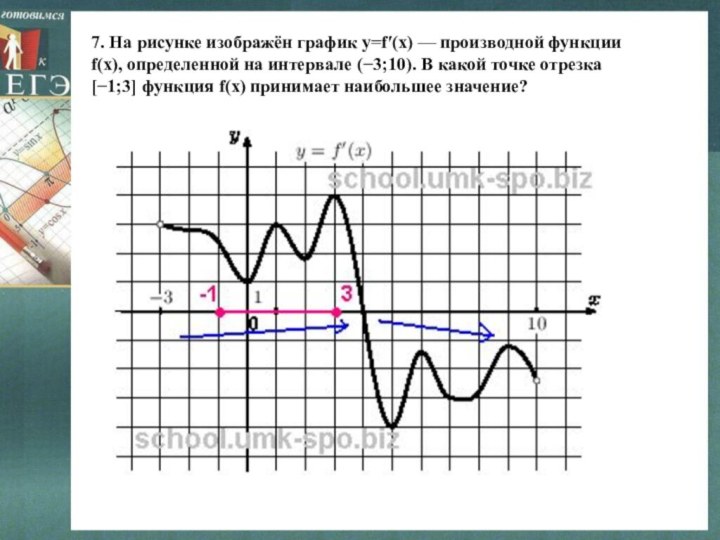
отрезка [−3;2] функция f(x) принимает наибольшее значение?Слайд 10 7. На рисунке изображён график y=f′(x) — производной
функции f(x), определенной на интервале (−3;10). В какой точке
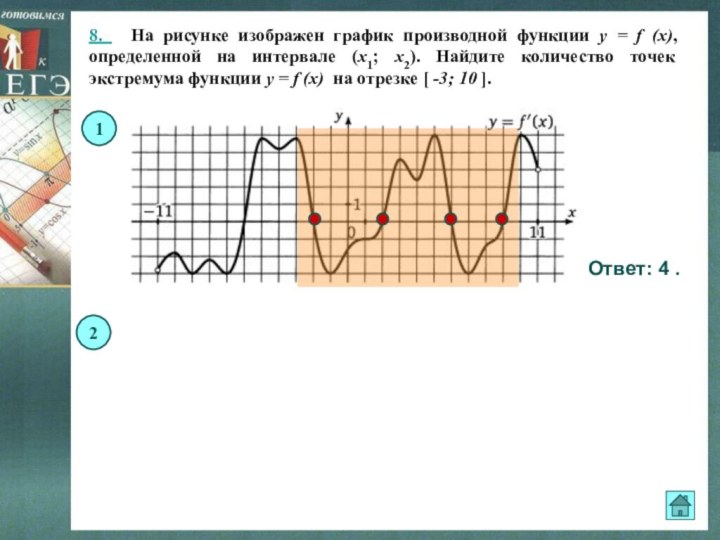
отрезка [−1;3] функция f(x) принимает наибольшее значение?Слайд 11 8. На рисунке изображен график производной функции
y = f (x), определенной на интервале (x1; x2).
Найдите количество точек экстремума функции y = f (x) на отрезке [ -3; 10 ].Ответ: 4 .
Ответ: 4 .
1
2
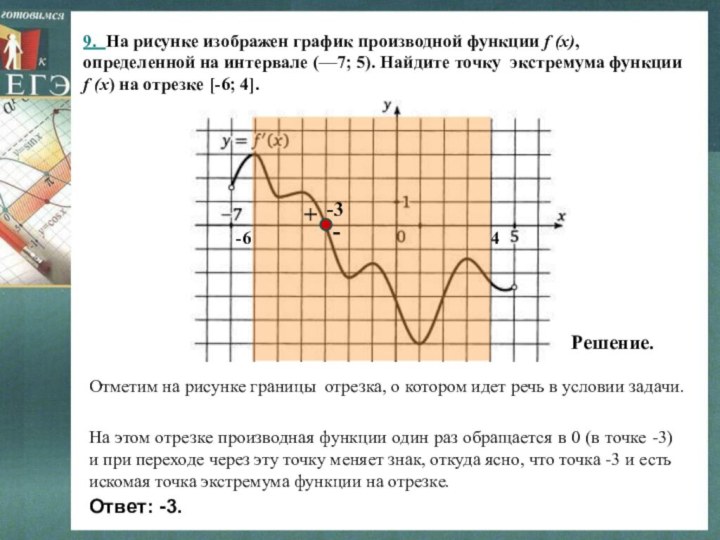
Слайд 12 9. На рисунке изображен график производной функции f
(x), определенной на интервале (—7; 5). Найдите точку экстремума
функции f (x) на отрезке [-6; 4].На этом отрезке производная функции один раз обращается в 0 (в точке -3) и при переходе через эту точку меняет знак, откуда ясно, что точка -3 и есть искомая точка экстремума функции на отрезке.
Решение.
Отметим на рисунке границы отрезка, о котором идет речь в условии задачи.
Ответ: -3.
-3
+
-
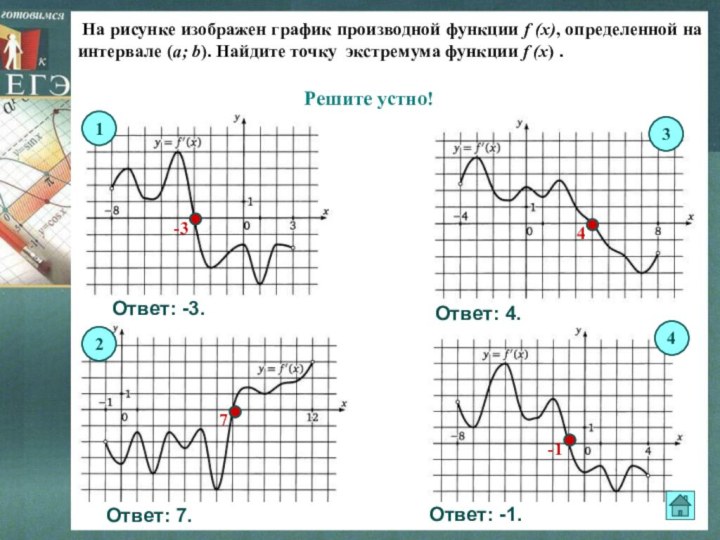
Слайд 13 На рисунке изображен график производной функции f
(x), определенной на интервале (a; b). Найдите точку экстремума
функции f (x) .Решите устно!
1
3
4
2
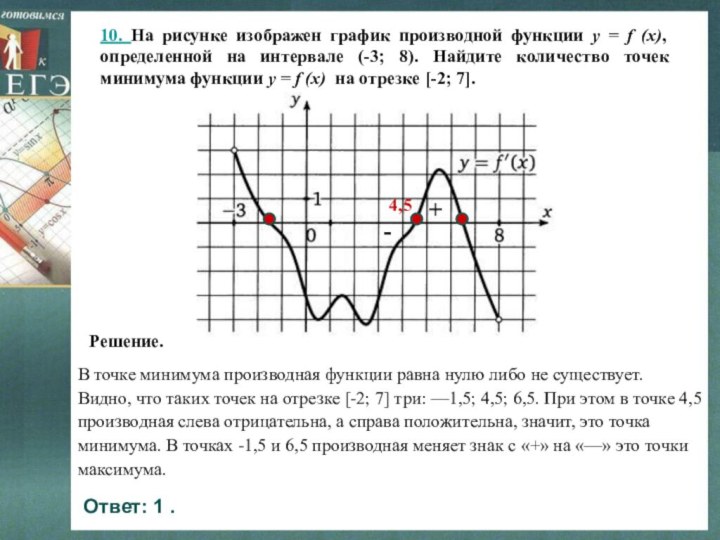
Слайд 14 В точке минимума производная функции равна нулю либо
не существует.
Видно, что таких точек на отрезке [-2;
7] три: —1,5; 4,5; 6,5. При этом в точке 4,5 производная слева отрицательна, а справа положительна, значит, это точка минимума. В точках -1,5 и 6,5 производная меняет знак с «+» на «—» это точки максимума.Решение.
Ответ: 1 .
4,5
-
+
10. На рисунке изображен график производной функции y = f (x), определенной на интервале (-3; 8). Найдите количество точек минимума функции y = f (x) на отрезке [-2; 7].
Слайд 15
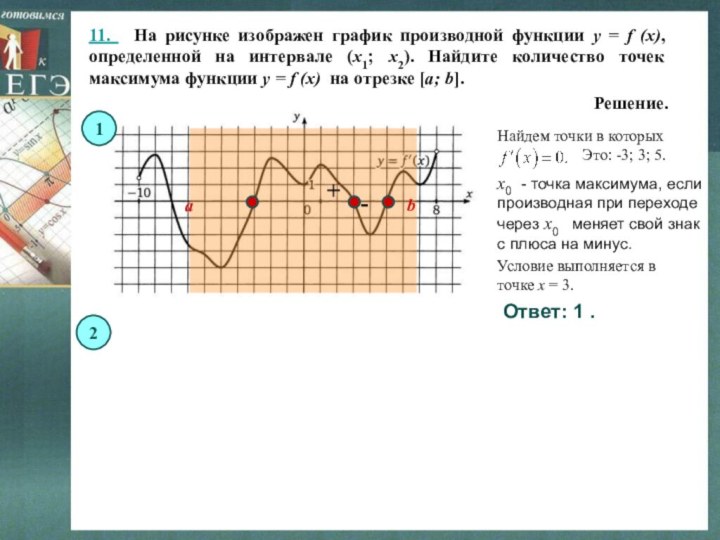
11. На рисунке изображен график производной функции
y = f (x), определенной на интервале (x1; x2).
Найдите количество точек максимума функции y = f (x) на отрезке [a; b].Решение.
Ответ: 1 .
Ответ: 3 .
a
b
a
b
x0 - точка максимума, если производная при переходе через x0 меняет свой знак с плюса на минус.
-
+
Условие выполняется в точке x = 3.
Решение.
Условие выполняется в точках: -1; 8; 13.
1
Решение аналогично.
2
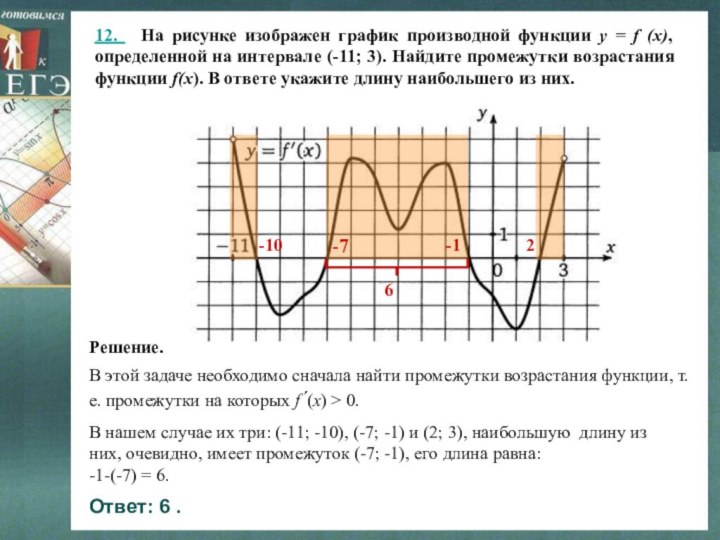
Слайд 16 12. На рисунке изображен график производной функции
y = f (x), определенной на интервале (-11; 3).
Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.В этой задаче необходимо сначала найти промежутки возрастания функции, т.е. промежутки на которых f´(x) > 0.
Решение.
В нашем случае их три: (-11; -10), (-7; -1) и (2; 3), наибольшую длину из них, очевидно, имеет промежуток (-7; -1), его длина равна:
-1-(-7) = 6.
Ответ: 6 .
-10
-7
-1
2
6
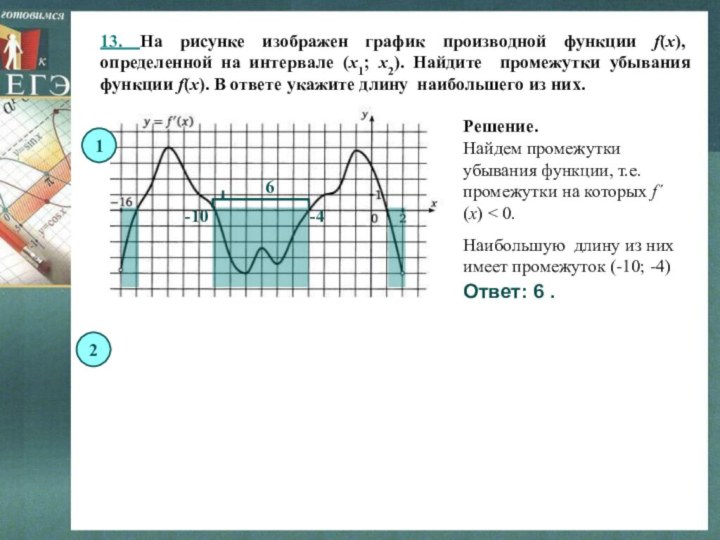
Слайд 17 13. На рисунке изображен график производной функции f(x),
определенной на интервале (x1; x2). Найдите промежутки убывания функции
f(x). В ответе укажите длину наибольшего из них.1
Решение.
Решение.
Ответ: 6 .
Ответ: 3 .
Найдем промежутки убывания функции, т.е. промежутки на которых f´(x) < 0.
Наибольшую длину из них имеет промежуток (-10; -4)
-10
-4
Решение аналогично: ищем промежутки на которых f´(x) < 0.
Наибольший из них имеет длину равную 3.
6
3
2
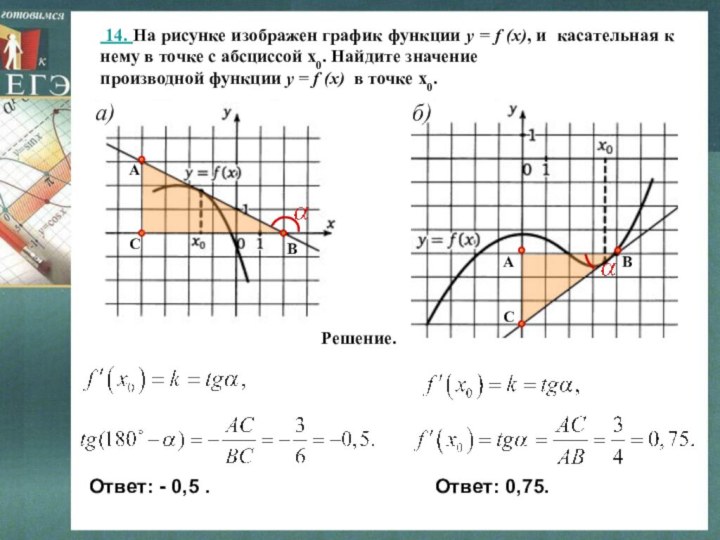
Слайд 18 14. На рисунке изображен график функции y
= f (x), и касательная к нему в точке
с абсциссой х0. Найдите значениепроизводной функции y = f (x) в точке х0.
Решение.
Ответ: - 0,5 .
Ответ: 0,75.
С
В
А
a)
б)
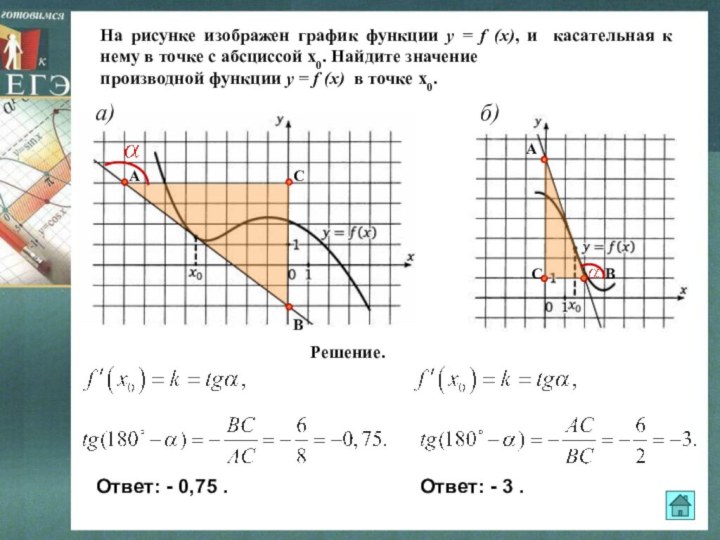
Слайд 19 На рисунке изображен график функции y = f
(x), и касательная к нему в точке с абсциссой
х0. Найдите значениепроизводной функции y = f (x) в точке х0.
Решение.
Ответ: - 0,75 .
А
В
С
А
В
С
Ответ: - 3 .
a)
б)
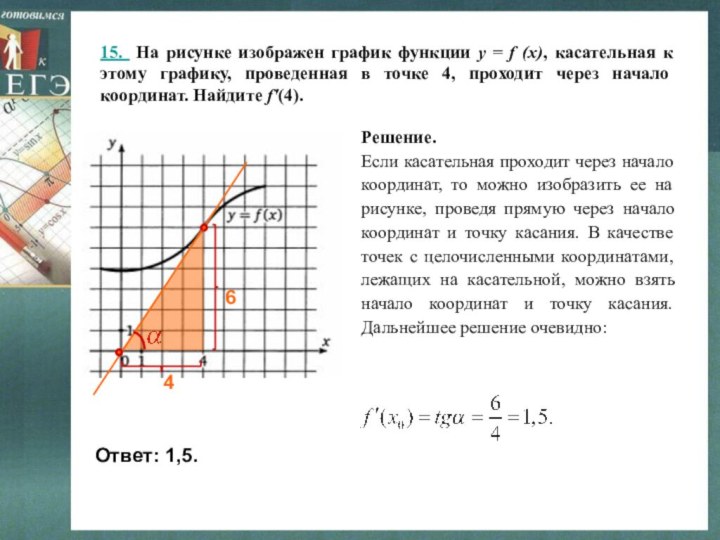
Слайд 20 15. На рисунке изображен график функции y =
f (x), касательная к этому графику, проведенная в точке
4, проходит через начало координат. Найдите f'(4).Решение.
Если касательная проходит через начало координат, то можно изобразить ее на рисунке, проведя прямую через начало координат и точку касания. В качестве точек с целочисленными координатами, лежащих на касательной, можно взять начало координат и точку касания. Дальнейшее решение очевидно:
Ответ: 1,5.
6
4
Слайд 21
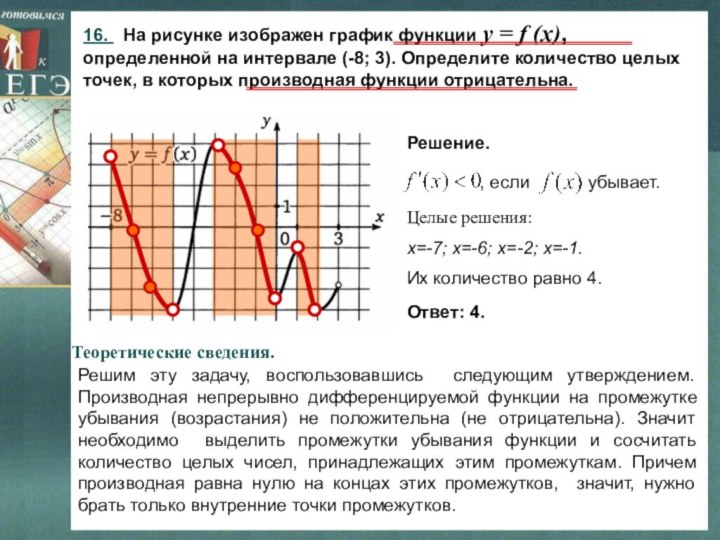
16. На рисунке изображен график функции y
= f (x),
определенной на интервале (-8; 3). Определите
количество целых точек, в которых производная функции отрицательна. Решим эту задачу, воспользовавшись следующим утверждением. Производная непрерывно дифференцируемой функции на промежутке убывания (возрастания) не положительна (не отрицательна). Значит необходимо выделить промежутки убывания функции и сосчитать количество целых чисел, принадлежащих этим промежуткам. Причем производная равна нулю на концах этих промежутков, значит, нужно брать только внутренние точки промежутков.
Решение.
Целые решения:
х=-7; х=-6; х=-2; х=-1.
Их количество равно 4.
Ответ: 4.
Теоретические сведения.
Слайд 22
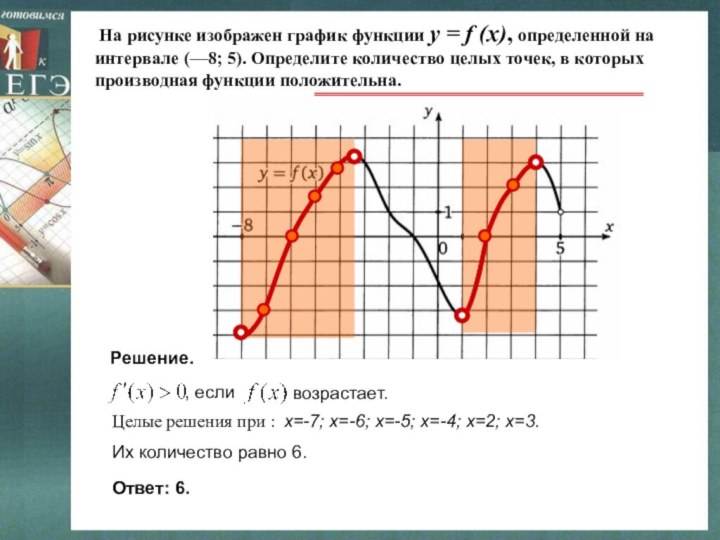
На рисунке изображен график функции y =
f (x), определенной на интервале (—8; 5). Определите количество
целых точек, в которых производная функции положительна.Решение.
Целые решения при : х=-7; х=-6; х=-5; х=-4; х=2; х=3.
Их количество равно 6.
Ответ: 6.
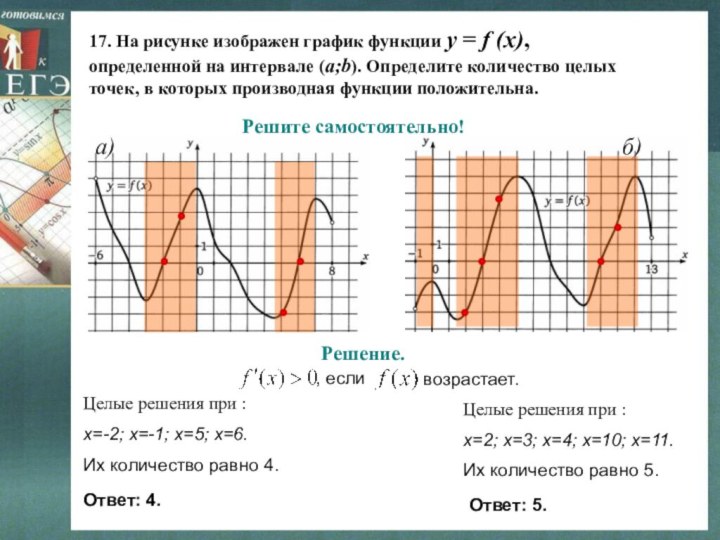
Слайд 23 17. На рисунке изображен график функции y =
f (x),
определенной на интервале (a;b). Определите количество
целых точек, в которых производная функции положительна.
a)
б)
Решите самостоятельно!
Решение.
Целые решения при :
х=-2; х=-1; х=5; х=6.
Их количество равно 4.
Целые решения при :
х=2; х=3; х=4; х=10; х=11.
Их количество равно 5.
Ответ: 4.
Ответ: 5.





























