Слайд 2
АБСОЛЮТНАЯ ВЕЛИЧИНА (АВ)
АВ – показатель, выражающий размеры социально-экономических
явлений числом единиц или величиной характеризующих их признаков в
данных условиях места и времени
АВ – количественный показатель, выражающий общую численность, размеры (объемы, уровни) и другие характеристики изучаемого процесса или явления
Слайд 3
ВИДЫ АБСОЛЮТНЫХ ВЕЛИЧИН (АВ)
индивидуальные
суммарные
Размер
заработной платы менеджера Загорских В.В.
Фонд оплаты труда сотрудников отдела
продаж
Слайд 4
ТИПЫ АБСОЛЮТНЫХ ВЕЛИЧИН (АВ)
Натуральные – такие единицы, которые
отражают величину предметов, вещей в физических мерах веса, объема,
площади и др.
Натуральный учет ведется в человеках, тыс. штук, т, м – в физических единицах измерения
Денежные (стоимостные) – используются для характеристики многих экономических показателей в стоимостном выражении
Трудовые – используются для определения затрат труда (человеко-час, человеко-день)
Условно-натуральные единицы - используются для сведения воедино нескольких разновидностей одинаковой потребительной стоимости.
Слайд 5
УСЛОВНО-НАТУРАЛЬНЫЕ ЕДИНИЦЫ
Перевод в условно - натуральное измерение производится
с помощью коэффициента пересчета. Для пересчета всех видов продукции
в сопоставимый вид используется некий эталон (баррель нефти, молоко 2,5% жирности)
Другие эталоны пересчета:
- моющие средства – в мыло 40%-ной жирности
консервные банки – в банки объемом 353,4 куб. см
- Топливо – в условное топливо с теплотой сгорания 29,3 МДж/кг
Если эталона нет, то его придумывают.
Слайд 6
АБСОЛЮТНАЯ ВЕЛИЧИНА (АВ)
Пример
Выпуск тетрадок, тыс. штук:
по 12
листов – 1000
по 24 листа – 200
по
48 листов – 50
по 96 листов - 100.
Определить выпуск продукции в пересчете на тетради по 12 листов
Решение
Слайд 7
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА (ОВ)
Абсолютные величины являются основой для расчета
разных относительных статистических показателей
Относительные величины в статистике представляют собой
частное от деления двух статистических величин и характеризуют количественное соотношение между ними
ОВ=А/Б
База сравнения
Если сравниваются одноименные величины, то результат выражается в коэффициентах (например 0,3), в процентах (30%) или промилле (300 0/00)
Относительная величина показывает, во сколько раз сравниваемая величина (А) больше или меньше базисной (Б) или какую долю первая (А) составляет по отношению ко второй (Б). В ряде случаев относительная величина показывает, сколько единиц одной величины (А) приходится на единицу другой (Б)
Важное свойство – относительная величина абстрагирует различия абсолютных величин и позволяет сравнивать такие явления, абсолютные размеры которых непосредственно несопоставимы
Слайд 8
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА (ОВ)
ОВ=А*100/Б
Чтобы перейти от % к коэффициентам,
ОВ делят на 100
Чтобы из коэффициентов получить проценты, ОВ
умножают на 100
ОВ=А*1000/Б
Промилле: лат. pro mille, т.е. на тысячу. Эта форма выражения ОВ обычно используется в демографической статистике
Чтобы перейти от промилле к коэффициентам, ОВ делят на 1000
Чтобы из коэффициентов получить промилле, ОВ умножают на 1000
Чтобы перейти от промилле к процентам,
ОВ делят на 10
Чтобы перейти от процентов к промилле,
ОВ умножают на 10
Слайд 9
ВИДЫ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН (ОВ)
Виды ОВ
ОВ планового задания
или
прогноза ОВПЗ
ОВ интенсивности ОВИ
ОВ выполнения
плана ОВВП
ОВ динамики ОВД
ОВ
координации ОВК
ОВ структуры ОВСтр
ОВ сравнения ОВС
Слайд 10
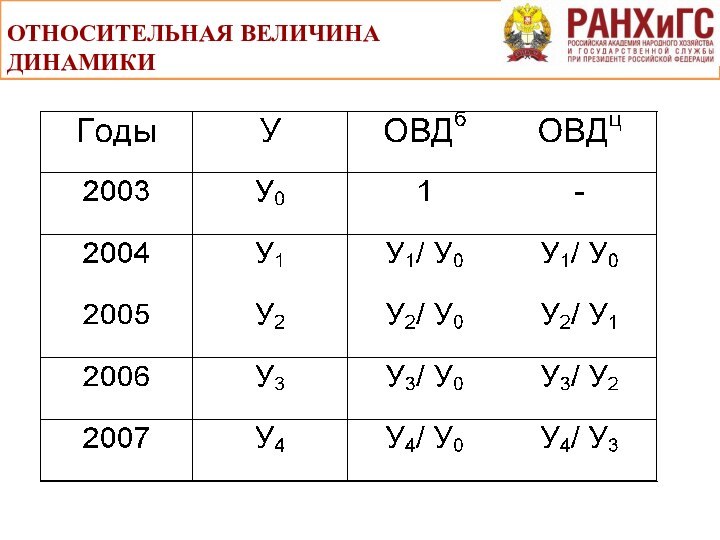
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ДИНАМИКИ
Относительная величина динамики ОВД представляет собой
отношение значений одного и того же показателя за разные
моменты или периоды времени.
где У1 – фактический показатель,
У0 – базисный
Слайд 11
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ДИНАМИКИ
Слайд 12
ВЗАИМОСВЯЗЬ ОВДц И ОВДб
если последовательно перемножить все цепные
величины, то мы получим базисную величину последнего периода:
если последующую
базисную величину разделить на предыдущую, то мы получим цепную величину последующего периода:
если последующую базисную величину разделить на цепную того же периода, получится предыдущая базисная величина:
Слайд 13
ВЗАИМОСВЯЗЬ ОВДц И ОВДб
ПРИМЕР. Реализация хлопчатобумажных тканей секцией
универмага составила в январе 3956 тыс. руб., в феврале
– 4200 тыс. руб., в марте – 4700 тыс. руб.
Темпы роста:
Базисные (база - уровень реализации в январе)
ОВДф/я = 4200 * 100% =106,3%
3950
ОВДм/я = 4700 * 100% =118,9%
3950
Цепные
ОВДф/я = 4200 * 100% =106,3%
3950
ОВДм/ф = 4700 * 100% =111,9%
4200
Слайд 14
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ПЛАНОВОГО ЗАДАНИЯ (ОВПЗ)
Относительные величины планового задания
ОВПЗ – отношение плана будущего периода к фактически достигнутому
уровню базисного периода:
где
-плановый уровень
- фактический уровень базисного периода
Показывает, во сколько раз планируют больше или меньше того, что достигнуто к плановому периоду
Слайд 15
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ВЫПОЛНЕНИЯ ПЛАНА (ОВВП)
Относительные величины выполнения плана
ОВВП характеризуют степень выполнения планового задания:
Слайд 16
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ВЫПОЛНЕНИЯ ПЛАНА (ОВВП)
ПРИМЕР В третьем квартале
товарооборот фирмы составил 150 млн руб. План на четвертый
квартал – 180 млн руб. Фактически товарооборот в четвертом квартале составил 202,5 млн руб. Рассчитать ОВД, ОВПЗ, ОВВП и показать их взаимосвязь:
y0=150 млн руб;
y1П=180 млн руб;
y1=202,5 млн руб
Взаимосвязь ОВД, ОВПЗ и ОВВП:
ОВД=ОВПЗ*ОВВП
1,35 =1,2 х 1,125
Слайд 17
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ВЫПОЛНЕНИЯ ПЛАНА (ОВВП)
ПРИМЕР. Прирост выпуска продукции
отрасли по плану на 2008 г. должен был составить
7,5 %. Фактический рост за 2008 год составил 109,5 %. Определить относительную величину выполнения плана по выпуску продукции.
ОВВП = 109,5 * 100% = 101,9 %
107,5
Слайд 18
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА СРАВНЕНЯ (ОВС)
Относительная величина сравнения (ОВС) представляет
собой соотношение одноименных величин, характеризующих разные объекты
Относительные величины сравнения
ОВС сравнивают значения одного и того же показателя, относящиеся к разным объектам
Пример. Запасы воды в озере Байкал-23000 куб. км, а в Ладожском озере 911куб.км
В нашем примере ОВС можно найти двояко:
ОВС1 = 911 = 0,0396
23 000
ОВС2 = 23 000 = 25,25
911
Слайд 19
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА ИНТЕНСИВНОСТИ (ОВИ)
Относительная величина интенсивности (ОВИ) –
отношение значений различных показателей, но взаимосвязанных и относящихся к
одному и тому же объекту
ОВИ характеризуют степень развития явления в данной среде
Число предприятий розничной торговли региона на конец года составило 6324. Численность населения данного региона на ту же дату составила 234,2 тыс. человек.
ОВИ = 6324 * 10 000 = 27,003
234 200
Единица измерения – предприятий на 10 тыс. чел. населения
Слайд 20
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА СТРУКТУРЫ (ОВС)
Относительная величина структуры представляет собой
соотношение частей и целого, характеризует структуру совокупности:
ОВС = часть целого
целое
Выражается в долях единиц или процентах, рассчитанных по одной совокупности. В сумме относительная величина структуры составляет 1 или 100%
ПРИМЕР Из общей численности населения России, равной на начало 2013г. 142 млн чел., 103,7 млн составляли городские жители, 38,3 млн – сельские.
Рассчитав ОВС, можно определить структуру населения по месту жительства:
Слайд 21
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА КООРДИНАЦИИ (ОВС)
Относительные величины координации (ОВК) представляют
собой соотношение частей целого между собой
ОВК=
ЧАСТЬ ЦЕЛОГО/ ДРУГАЯ ЧАСТЬ ЦЕЛОГО
Выражаются в долях единиц (допускается домножение на 10, 100 (если этого требует логика – не может быть соотношение людей 1 к 1,5 , может 10 к 15...)
ОВК применяется для дополнительной характеристики структуры (например, количество женщин, приходящееся на 1000 мужчин и наоборот)
На начало года численность специалистов с высшим образованием, занятых в ассоциации «Торговый дом», составила 53 человека, а численность специалистов со средним образованием - 106 человек
Принимаем за базу сравнения численность специалистов с высшим образованием:
ОВК = 106/53 = 2,0:1,0,
т.е на двух специалистов со средним специальным образованием приходится один с высшим
Слайд 22
ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА УРОВНЯ ЭКОНОМИЧЕСКОГО РАЗВИТИЯ (ОВУЭР)
Относительная величина уровня
экономического развития характеризует размеры производства различных видов продукции на
душу населения. В знаменателе фигурирует «душа» - среднегодовая численность населения
Слайд 24
ЧТО ТАКОЕ СРЕДНЯЯ ВЕЛИЧИНА И КАК ОНА ОТРАЖАЕТ

СОВОКУПНОСТЬ?
Средней величиной называют показатель, который характеризует обобщенное значение признака
или группы признаков в исследуемой совокупности.
Средняя величина заменяет большое число индивидуальных значений признака, обнаруживая общие свойства, присущие всем единицам совокупности.
Среднее - такое значение признака, которое имело бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности.
Средняя величина — это обобщающая характеристика размера изучаемого признака. Она позволяет одним числом количественно охарактеризовать качественно однородную совокупность.
Средняя величина должна быть типична, а измеряемая ею совокупность - однородна
Совокупность должна быть однородной, не распадающейся на несколько самостоятельных совокупностей
Средняя вычисляется для признаков, присущих всем членам совокупности, для признаков, качественно однородных и различающихся только количественно
Объективность средней определяется достаточно большим числом единичных измерений, составляющих совокупность
Рассчитываются на основе массовых данных – достаточного числа анализируемых единиц.
Достаточность анализируемых единиц обеспечивается корректным определением границ исследуемой совокупности.
Слайд 25
СВОЙСТВА СРЕДНЕЙ
Важнейшее свойство средней величины заключается в том,
что она выражает то общее, что присуще всем единицам
исследуемой совокупности:
Типичность средней зависит от степени однородности совокупности. Сумма отклонений от среднего равно 0:
Слайд 26
ЛОГИЧЕСКАЯ ФОРМУЛА СРЕДНЕГО
Определить среднее во многих случаях можно
через исходное соотношение средней:
Средняя заработная плата:
Средний размер банковского вклада:
Слайд 27
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ПРОСТАЯ – это такое значение
признака, при вычислении которого общий объем признака в совокупности
сохраняется неизменным
Xi – Значение варьирующего признака, n – число значений этого признака
Пример. Рассчитайте среднюю почасовую ставку заработной платы рабочих, если по имеющимся данным они получают 135, 141, 153, 159, 162 руб.
Решение:
Средняя почасовая ставка составит:
Слайд 28
Пример. Необходимо определить средний тарифный разряд рабочих по
данным
Решение: Изучаемый признак - тарифный разряд, частота - число
рабочих, тогда
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЗВЕШАННАЯ– рассчитывается по-разному для дискретного (прерывающегося) и интервального (непрерывного) ряда.
Для ДИСКРЕТНОГО ряда:
fi – частота повторения соответствующего значения признака
Слайд 29
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
Средняя арифметическая взвешанная– рассчитывается по-разному для дискретного
(прерывающегося) и интервального (непрерывного) ряда.
Для ИНТЕРВАЛЬНОГО ряда:
х’i – среднее
значение интервала, т.е. полусумма его верхней и нижней границ
Пример. Необходимо рассчитать среднесуточный пробег автомобилей
Решение: Рассчитаем полусуммы для каждого интервала (т.е. середины):
тогда
и т.д.
Слайд 30
Пример. Определим среднюю часовую заработную плату работников в
среднем по предприятию
Решение:
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
Арифметическая средневзвешанная– применяется для вычисления
общей средней из частных групповых средних.
– частные групповые средние
Слайд 31
Пример. Определим среднесуточную зарплату одного рабочего
Решение:
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ
Средняя
гармоническая– это величина, обратная средней арифметической. Она применяется, когда
в данных в явном виде отсутствует частота.
– суммарное значение признака по группе i
Слайд 32
СРЕДНЯЯ КВАДРАТИЧЕСКАЯ
Средняя квадратическая применяется, когда осреднению подлежат функции,
выраженные в виде квадратных величин.
Слайд 33
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ
Средняя геометрическая применяется, когда осреднению подлежат функции,
выраженные в виде квадратных величин.
Всегда следует помнить, что
Применение
конкретной формулы зависит от вида имеющихся данных
Слайд 34
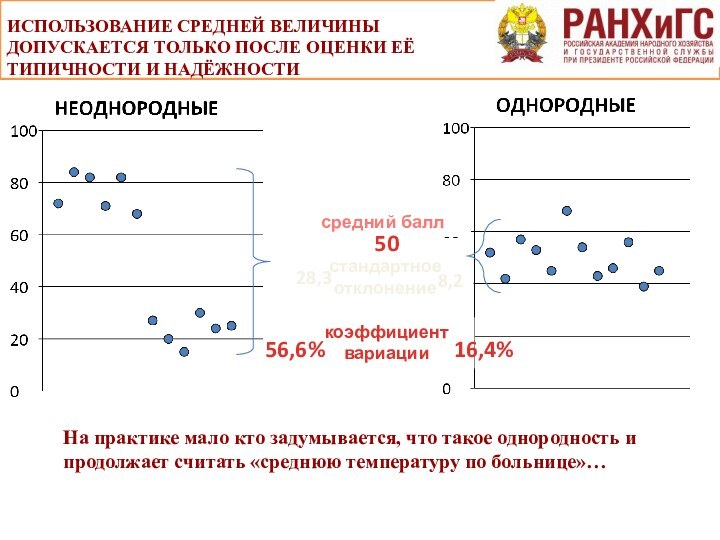
ИСПОЛЬЗОВАНИЕ СРЕДНЕЙ ВЕЛИЧИНЫ ДОПУСКАЕТСЯ ТОЛЬКО ПОСЛЕ ОЦЕНКИ ЕЁ
ТИПИЧНОСТИ И НАДЁЖНОСТИ
средний балл
50
стандартное отклонение
28,3
8,2
коэффициент вариации
56,6%
16,4%
На практике мало кто
задумывается, что такое однородность и продолжает считать «среднюю температуру по больнице»…
Слайд 36
Напомним, что при упорядоченном распределении единиц совокупности по
возрастанию или убыванию значений признака получают вариационный ряд.
Его
характеризует ряд показателей:
Показатели центра распределения – средняя арифметическая, структурные средние (мода и медиана);
Ранговые характеристики- квартили, децили;
Показатели вариации;
Показатели формы распределения
Слайд 37
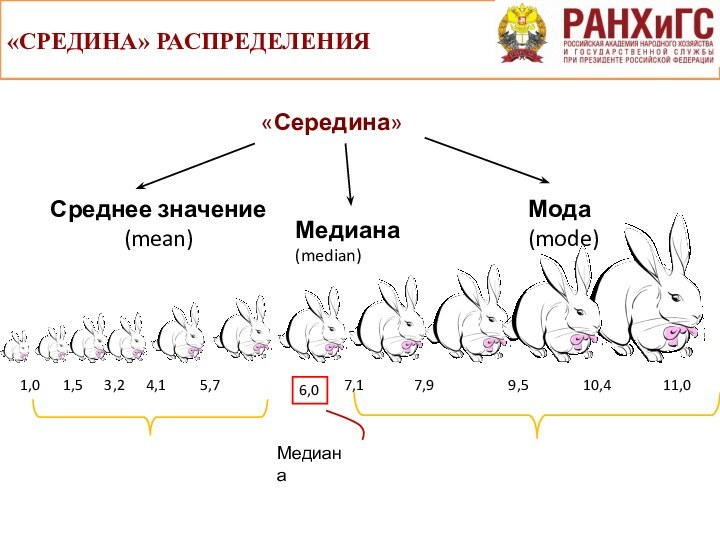
«СРЕДИНА» РАСПРЕДЕЛЕНИЯ
«Середина»
Мода
(mode)
Медиана (median)
Среднее значение (mean)
1,0
1,5
4,1
5,7
9,5
6,0
7,1
7,9
10,4
11,0
3,2
Медиана
Слайд 38
СТРУКТУРНЫЕ СРЕДНИЕ
Мода ряда распределения – значение признака наиболее
часто встречающееся в исследуемой совокупности
Медиана ряда распределения – значение
признака, приходящееся на середину ранжированной (упорядоченной) по данному признаку совокупности
Для дискретного вариационного ряда:
Модой будет вариант признака с наибольшей частотой
Медианой будет:
- для ряда с нечетным числом членов – центральный вариант, находящийся в середине ранжированной совокупности
- для ряда с четным числом членов – среднее значение из двух соседних центральных вариантов
Слайд 39
ПРИМЕРЫ МОДЫ И МЕДИАНЫ
Мода ряда распределения объема продаж
(частота) размеров женской обуви:
Медиана ряда распределения по уровню
ежемесячного дохода 11 человек:
Слайд 40
РАСЧЕТ МОДЫ И МЕДИАНЫ ПО ИНТЕРВАЛЬНЫМ РЯДАМ РАСПРЕДЕЛЕНИЯ
Мода
составляет: 26,2
Слайд 41
РАСЧЕТ МОДЫ И МЕДИАНЫ ПО ИНТЕРВАЛЬНЫМ РЯДАМ РАСПРЕДЕЛЕНИЯ
Медиана
составляет: 37
Слайд 42
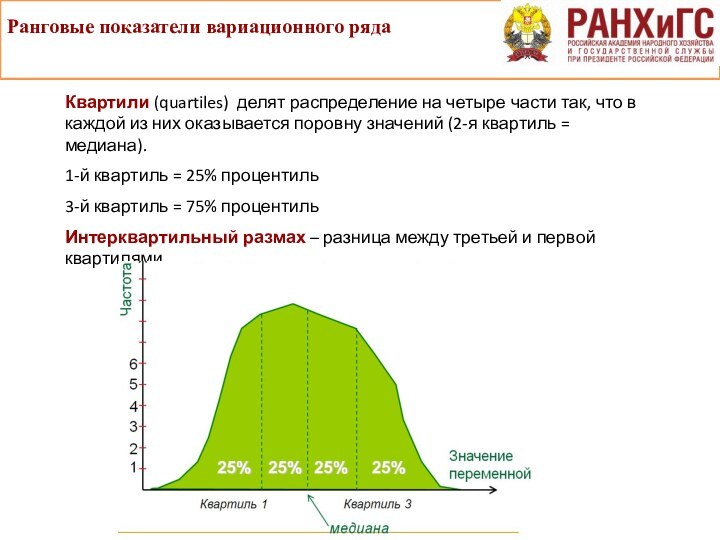
Квартили (quartiles) делят распределение на четыре части так,
что в каждой из них оказывается поровну значений (2-я
квартиль = медиана).
1-й квартиль = 25% процентиль
3-й квартиль = 75% процентиль
Интерквартильный размах – разница между третьей и первой квартилями.
Ранговые показатели вариационного ряда
Слайд 43
РАСЧЕТ КВАРТИЛЕЙ
Для определения 1-ого квартиля:
Для определения 3-ого
квартиля:
Где и
- нижние границы
интервалов, в которые попадают соответствующие квартильные значения;
и сумма накопленных частот до соответствующего интервала;
частота соответствующего квартильного интервала
Слайд 44
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Пусть дан следующий вариационный ряд:
Размах
вариации:
Слайд 45
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Так как величина размаха характеризует
только максимальное различие значений признака, не измеряя при этом
степень вариации этого признака во всей совокупности, на практике этот показатель используется только при расчете предупредительного контроля качества продукции. Применение этого показателя ограничено только однородными совокупностями, так как он зависит от величины только крайних значений
Среднее линейное отклонение (d) - характеризует среднюю величину, на которую основная масса единиц совокупности отклоняется от среднего значения.
Для несгруппированных данных
Для сгруппированных данных
Слайд 46
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Дисперсия – это средняя из
квадратов отклонений вариантов признака от их средней величины. Это
средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней.
Она рассчитывается по простой и взвешенной формулам. Для ее обозначения используется греческая буква сигма.
Свойства дисперсии:
Дисперсия постоянной величины равна 0
Если все варианты значений признака уменьшить на одно и то же число, то дисперсия не уменьшится
Если все варианты значений признака уменьшить в одно и то же число раз z, то дисперсия уменьшится в z2 раз
Для несгруппированных данных
Для сгруппированных данных
Слайд 47
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Слайд 48
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Слайд 49
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Расчет дисперсии упрощенным способом осуществляется
на основе перечисленных свойств по формуле:
, где
Слайд 50
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Слайд 51
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Слайд 52
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ) ПРИЗНАКА
Недостаток дисперсии состоит в том,
что она имеет размерность вариант, возведенную в квадрат (рублей
в квадрате, человек в квадрате)
Чтобы устранить этот недостаток, используется среднее квадратическое отклонение
Слайд 53
ПОКАЗАТЕЛИ ВАРИАЦИИ (РАССЕЯНИЯ)
Среднее квадратическое отклонение – это корень
квадратный из дисперсии.
Для несгруппированных данных
Для сгруппированных данных
В соответствии
с теоремой П.Л. Чебышева, можно утверждать, что независимо от формы распределения 75% значений признака попадают в интервал , а по крайней мере 89% всех значений попадают в интервал
Слайд 54
ОТНОСИТЕЛЬНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ
При сравнении вариации различных признаков одной
и той же совокупности пользуются относительными показателями вариации:
Коэффициент осцилляции
Относительное
линейное отклонение
Коэффициент вариации
Слайд 55
КОЭФФИЦИЕНТ ОСЦИЛЛЯЦИИ
где
R - размах вариации
- среднее значение
Коэффициент
осцилляции отражает относительную колеблемость крайних значений признака относительно среднего
значения
Слайд 56
ОТНОСИТЕЛЬНОЕ ЛИНЕЙНОЕ ОТКЛОНЕНИЕ
где
- среднее линейное отклонение
Слайд 57
КОЭФФИЦИЕНТ ВАРИАЦИИ
Характеризует долю усредненного значения отклонений от средней
величины. При этом совокупность считается однородной, если V
не превышает 33%
Слайд 58
Дисперсия альтернативного признака
Слайд 59
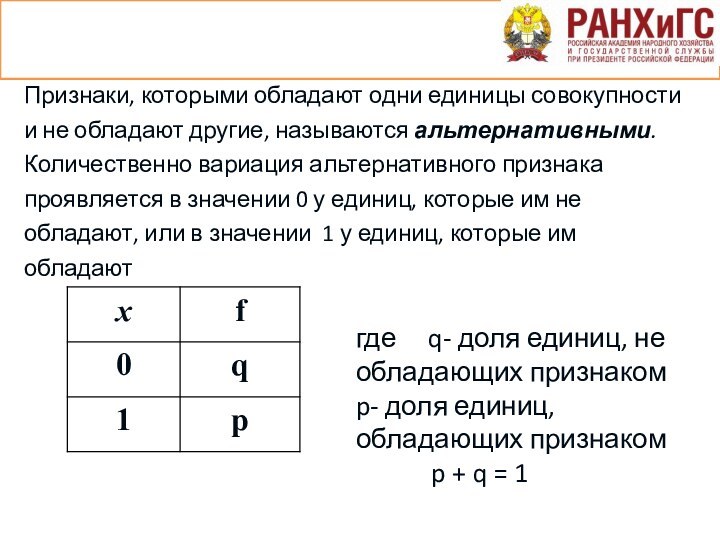
Признаки, которыми обладают одни единицы совокупности и не
обладают другие, называются альтернативными. Количественно вариация альтернативного признака проявляется
в значении 0 у единиц, которые им не обладают, или в значении 1 у единиц, которые им обладают
где q- доля единиц, не обладающих признаком
p- доля единиц,обладающих признаком
p + q = 1
Слайд 60
Среднее значение альтернативного признака
Слайд 61
Дисперсия альтернативного признака :
Максимальное значение дисперсии альтернативного признака
0,25
Слайд 62
Среднее квадратическое отклонение альтернативного признака :
Коэффициент вариации альтернативного
признака:
Слайд 63
1) общую
2) межгрупповую
3) внутригрупповую
Выделяют дисперсии:
Слайд 64
Величина общей дисперсии характеризует вариацию признака под воздействием
всех факторов, вызывающих эту вариацию:
где j – номер варианты
Слайд 65
Межгрупповая дисперсия (дисперсия групповых средних или факторная дисперсия)
характеризует систематическую вариацию, т. е. различия в величине изучаемого
признака, возникающие под влиянием одного фактора, положенного в основание группировки
Слайд 66
где
– среднее значение
изучаемого признака для i – й
группы
- номер группы
– количество единиц в i – й группе
Слайд 68
Внутригрупповая (средняя из групповых или остаточная) дисперсия характеризует
случайную вариацию, т. е. ту часть вариации, которая вызвана
действием других неучтённых факторов, и не зависящую от фактора, положенного в основании группировки:
Слайд 70
Общая дисперсия равна сумме межгрупповой и внутригрупповой дисперсий:
Слайд 71
ТЕМА
ВЫБОРОЧНЫЙ МЕТОД (ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ)
Слайд 72
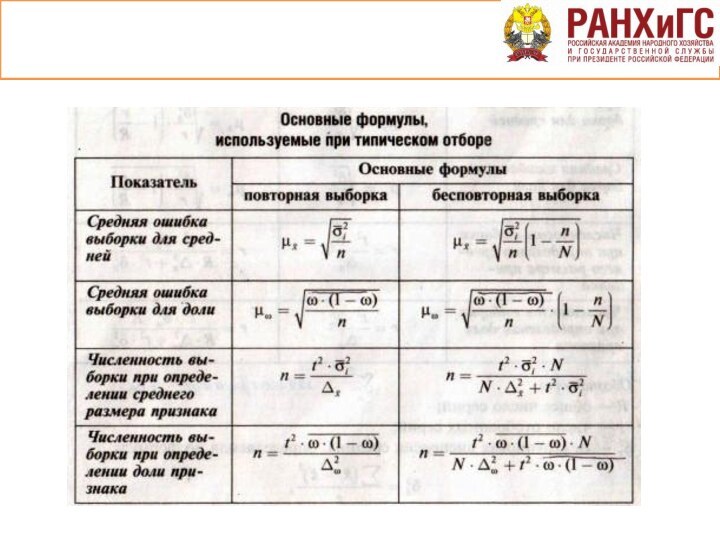
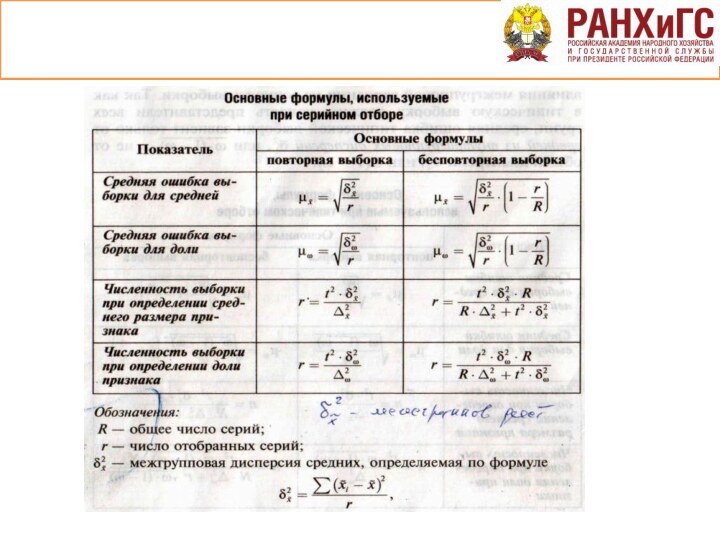
Выборочные наблюдения – такое несплошное наблюдение, при котором
статистическому исследованию подвергаются не все единицы изучаемой совокупности, а
лишь отобранные по определенным правилам и в определенном порядке.
p=
,
Слайд 73
Ошибка репрезентативности – расхождение между выборочной характеристикой и
характеристикой генеральной совокупности.
Ошибки репрезентативности