Презентация на тему АВТОРЕГРЕССИОННЫЕ МОДЕЛИ

факторных признаков, содержит одно или больше предыдущих значений зависимой

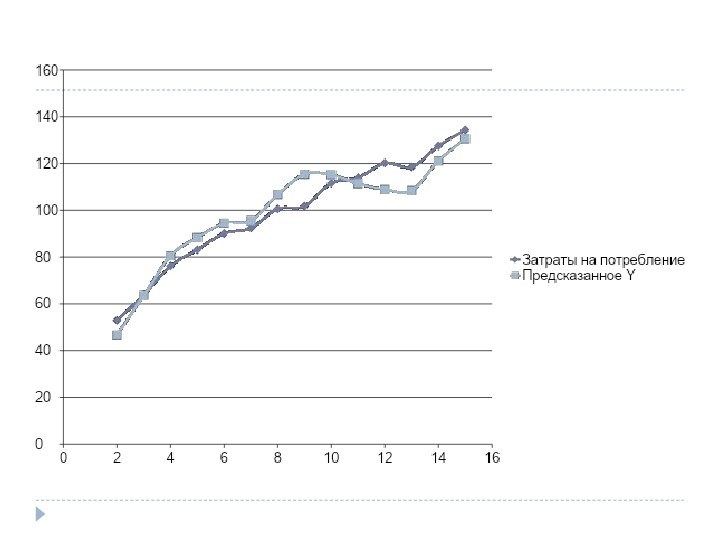
переменной

Авторегрессионные модели также называют динамичными моделями, так как они отображают временные изменения результирующей (зависимой) переменной относительно ее предыдущих значений

присутствуют стохастические переменные (зависимые)

Возможна автокорреляция

преобразования;

Метод скользящих средних;

Метод, учитывающий смешанную модель авторегрессии и скользящих

средних

, для которой нарушается предпосылка применения

метода наименьших квадратов, заменяется на новую переменную z, которая сильно коррелирует с , но не коррелирует с .
Выбираются переменные , от которых зависит
. Строится регрессия вида:

Обычным методом наименьших квадратов оцениваются ее параметры . Выражение обозначается как .

преобразованной модели, в которой

заменяются на , рассчитываются с помощью традиционного метода наименьших квадратов. Эти оценки будут являться оценками неизвестных коэффициентов исходной модели автокорреляции

переменные для лаговых значений результирующей переменной

и величинах дохода
Необходимо построить авторегрессионную модель зависимости между данными

показателями

не только от величины дохода текущего года, но от

затрат на потребление предыдущего периода

0,915 - 91,5% изменения затрат на потребление объясняется выбранными

параметрами: уровнем дохода и затратами на потребление предыдущего года

построения уравнения регрессии типа



Параметры данного уравнения

величин случайных составляющих